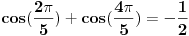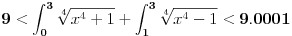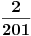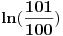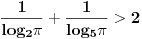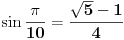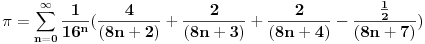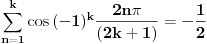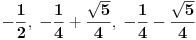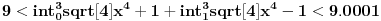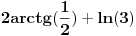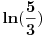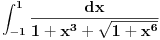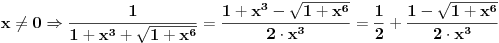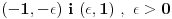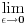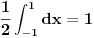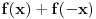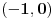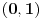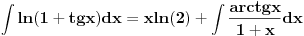[ stalker @ 04.01.2004. 23:27 ] @
|
[ noviKorisnik @ 05.01.2004. 08:41 ] @
Odgovor na 3. pitanje:
(a) 2 2 2 nisu mogući početni brojevi (b) 3 3 3 jesu mogući početni brojevi [ goky2002 @ 05.01.2004. 16:39 ] @
1.
Malo sam izasao iz stosa ali mislim da moze ovako: cos(2pi/5) + cos(4pi/5) = cos(2pi/5) + 1-2(cos(2pi/2))^2 neka je x=cos(2pi/2) onda resavamo jednacinu x+1-2x^2 = -1/2 jedno resenje je -1/2 drugo je vece od 1 tako da ostaje da cos(2pi/5) =-1/2 [ blaza @ 06.01.2004. 00:56 ] @
Prvi zadatak je trivijalan.
Drugi zadatak: Kak`a je ovo dlaka? - rece ekonomista kad vidi integral. Jel se integrali po x, (nisi naznacio)? Treci zadatak. Broj 17 je zadnji put menjan kada su druga dva broja bili manji od 17, kada im je zbir bio 18. Znaci, druga dva broja su povecana odredjen broj puta sa 16. Ako druga dva broja smanjimo za 16, dovoljan broj puta, da budu manji od 17, imacemo: 17 15 15. Posto je najveci broj uvek onaj koji je zamenjen u prethodnoj akciji, a kako iz 17 15 15 ne sledi ni jedna validna akcija koja prethodi, jednom broju 15 dodacemo 16, te imamo: 17 15 31 ili 17 31 15. Validne akcije koje su prethodile ovim su: 17 15 3 odnosno 17 3 15. Validne akcije koje su prethodile ovim su: 13 15 3 odnosno 13 3 15. Validne akcije koje su prethodile ovim su: 13 11 3 odnosno 13 3 11. Validne akcije koje su prethodile ovim su: 9 11 3 odnosno 9 3 11. Validne akcije koje su prethodile ovim su: 9 7 3 odnosno 9 3 7. Validne akcije koje su prethodile ovim su: 4 7 3 odnosno 4 3 7. Kako nema validnih akcija koje prethode ovim, to su jedine pocetne pozicije od kojih se mogu dobiti date vrednosti, pa su odgovori pod a i b : NE (Ako nisam nesto prevideo) Cetvrti zadatak: ln(101/100)=suma(n=0, beskonacno, (-1)^n / ((n+1)*100^(n+1))=1/100-1/20000+1/3000000-1/400000000+... 2/201=1/100-1/20100=1/100-1/20000+1/4020000=1/100-1/2000+1/3000000-51/603000000=... Posto za n=2k i n=2k+1 sumi dodajemo: 1/((n+1)*100^(n+1))-1/((n+2)*100^(n+2))=1/100^(n+1) * (1/(n+1)-1/(100*(n+2)))= 1/100^(n+1) * ((100*(n+2)-(n+1))/(100(n+1)(n+2)) >0 Tada imamo: ln(101/100)=1/100-1/20000+1/3000000-1/400000000 + pozitivne vrednosti posto su upareni clanovi sume pozitivni a 2/201=11/100-1/2000+1/3000000-51/603000000 i kako je 1/400000000 manje od 51/603000000, a prvoj sumi se dodaju samo jos pozitivne vrednosti, tada je ln(101/100) veci od 2/201. Peti zadatak 1/log(2,Pi)+1/log(2,Pi)=(ln(2)+ln(5))/ln(Pi)>2 => ln(10)>2 ln (Pi) = ln (Pi^2) => 10> Pi^2 Da li je sada potrebno dokazati da je Pi^2 manje od 10? Evo, da ja zabiberim udarac: Zadatak 6. Dokazati: Pi=suma(n=0, beskonacno,(4/(8n+2)+2/(8n+3)+2/(8n+4)-0.5/(8n+7))/16^n) [Ovu poruku je menjao blaza dana 06.01.2004. u 09:55 GMT] [ noviKorisnik @ 06.01.2004. 01:21 ] @
Treće pitanje, drugi put:
Zašto (b) 3 3 3 jesu mogući početni brojevi ? Mali pametni algoritam: - fiksirati jednu trojku dok se ne dobije 17. (pozicija 3 15 17) - izbrisati trojku. - fiksirati sedamnaesticu i voziti do kraja (odnosno 17 1967 1983) Zašto (a) 2 2 2 nisu mogući početni brojevi ? 1. prisutna su 3 parna broja. 2. jedan se briše i po računici se dobija neparni broj. 3. prisutna su 2 parna i 1 neparan broj. 4a. briše se jedan paran broj i po računici se ponovo dobija parni broj. 4b. briše se jedini neparni broj i po računici se ponovo dobija neparni broj. 5. aj ponovo na tačku 3. Ovo nikada neće dovesti do 3 neparna broja (recimo 17 1967 1983) [ noviKorisnik @ 06.01.2004. 01:29 ] @
Citat: blaza: 9 7 3 odnosno 9 3 7. Validne akcije koje su prethodile ovim su: 4 7 3 odnosno 4 3 7. ... 9 7 3 odnosno 9 3 7. Validne akcije koje su prethodile ovim su: 5 7 3 odnosno 5 3 7. Validna akcija koja je prethodila ovoj je: 5 3 3. Validna akcija koja je prethodila ovoj je: 3 3 3. [ blaza @ 06.01.2004. 01:51 ] @
Svaka cast novikorisnice.
Nikada mi racunanje na prste nije islo od ruke :) Dobro sto sam rekao: Citat: , pa su odgovori pod a i b : NE (Ako nisam nesto prevideo) [ anon315 @ 06.01.2004. 08:54 ] @
Au bre Blazo,
nisam ti obrisao poruku samo zato što si se potrudio da je ispišeš. Zamolio bih te da, iako to nije obavezno, pogledaš sledeću temu: http://www.elitesecurity.org/tema/35291 Ipak je malo mučno čitati ovako nešto: Citat: ln(101/100)=suma(n=0, beskonacno, (-1)^n / ((n+1)*100^(n+1)) Citat: Drugi zadatak: Kak`a je ovo dlaka? - rece ekonomista kad vidi integral. Jel se integrali po x, (nisi naznacio)? A toliko možeš valjda i sam da zaključiš ? [ stalker @ 06.01.2004. 11:41 ] @
[ Mihailo Kolundzija @ 06.01.2004. 12:35 ] @
[ blaza @ 06.01.2004. 12:48 ] @
Citat: Vanja Petreski: Au bre Blazo, nisam ti obrisao poruku samo zato što si se potrudio da je ispišeš. Zamolio bih te da, iako to nije obavezno, pogledaš sledeću temu: U redu. Primedba je opravdana. [ stalker @ 06.01.2004. 14:54 ] @
Citat: goky2002: 1. Malo sam izasao iz stosa ali mislim da moze ovako: cos(2pi/5) + cos(4pi/5) = cos(2pi/5) + 1-2(cos(2pi/2))^2 neka je x=cos(2pi/2) onda resavamo jednacinu x+1-2x^2 = -1/2 jedno resenje je -1/2 drugo je vece od 1 tako da ostaje da cos(2pi/5) =-1/2 Nisam tu da ocenjujem, ali ovo mi lici na nesto bezveze napisano. @blaza Zasto ti se cini da je prvi zadatak trivijalan??? Mihailo je bio najblizi, cini mi se, samo treba dokazati to sto je on rekao. BTW, ove zadatke sam nasao na nekom starom disku koji sam rezao (pre 3-4 godina) sa olimpijade/a (ne znam tacno) i na tom sajtu nisu davali resenja. Ne znam sajt vise, ne znam ni resenja, tako da cu da vam se, momci, pridruzim cim se zavrsi rok:) [ blaza @ 06.01.2004. 15:20 ] @
[ stalker @ 06.01.2004. 17:31 ] @
Ovo je ipak malo zanimljivije od rokova:)
Hvala Mihajlu na savetu Uz pomoc 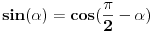 dobija se dobija se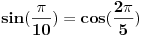 Kada sada krenemo sa druge strane, da izrazimo ovo, dobija se: 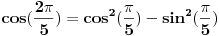 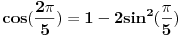 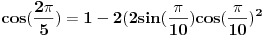 Kad uvedemo smenu 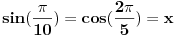 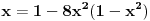 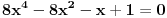 Vidi se da je jedno resenje  pa se dobija, kad se ono izbaci pa se dobija, kad se ono izbaci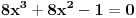 Ja ne znam ovo da resim, nadam se da nije tesko, zna li neko? P.S. Proverio sam, iz ovoga se dobija tacno resenje za x koje, kad se ubaci dokazuje zadatak P.S.S. Ma jesu za osnovce, sigurno;) [ Mihailo Kolundzija @ 06.01.2004. 19:11 ] @
Ovo možeš da malo olakšaš zamenom 2x = a. Tada dobijaš 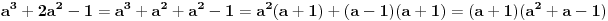 Ostatak je valjda lak. (kosinus je parna funkcija, pa je onaj 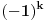 višak) višak)Zbir ovih silnih kosinusa možemo da udvostučimo, dodajući sumu 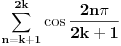 i kad na sve to dodamo jedinicu, zadatak nam se svodi na dokaz da je nova velika suma ravna nuli. Kako je svima nam očigledno, ova je suma ustvari realni deo sume korena jednačine 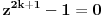 a pošto i svi znamo da je ta suma jednaka nuli za k > 0 (to nam može reći, na primer, čika Vijet), to je i naš zadatak dokazan. [ goky2002 @ 06.01.2004. 21:48 ] @
.... > Citat: *goky2002:* > 1. > Malo sam izasao iz stosa ali mislim da moze ovako: > > cos(2pi/5) + cos(4pi/5) = cos(2pi/5) + 1-2(cos(2pi/2))^2 > > neka je x=cos(2pi/2) > > onda resavamo jednacinu x+1-2x^2 = -1/2 > > jedno resenje je -1/2 drugo je vece od 1 tako da ostaje da cos(2pi/5) =-1/2 > > > Citat: *stalker:* > Nisam tu da ocenjujem, ali ovo mi lici na nesto bezveze napisano. Mozda je i bezveze ali onda treba reci zasto je bezveze. Ja sam pisao ono sto mi je trenutno u glavi. Rekoh da sam izasao iz stosao. Uzgred ima greska u kucanju cos(2pi/5) + cos(4pi/5) = cos(2pi/5) + 1-2(cos(2pi/5))^2 neka je x=cos(2pi/5) [ filmil @ 06.01.2004. 23:12 ] @
Nije teško da se vidi da su u oblasti 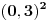 podintegralne podintegralnefunkcije jedna drugoj inverzi. Zato su površine koje se nalaze unutar pomenute oblasti, a iznad prve, odn. ispod druge podintegralne funkcije zapravo jednake (simetrija). Označimo te površine sa A. Površine iznad druge podintegralne funkcije a ispod funkcije x=y i iznad x=y a ispod prve su jednake. Označimo ih sa B. Očigledno je da je 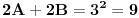 . .Zbir integrala ima još i oblast C koja se nalazi iznad prave y=3. Ceo zbir iznosi (A+2B+C)+A = 2A+2B+C što je sada očigledno veće od 9, pa je prvi deo nejednakosti dokazan. Ostaje da se pokaže da je C<0.0001, što nije teško ako se uoči da je prva podintegralna funkcija konveksna tako da je površina C manja od površine trougla koga čine tačke (3,3) i mesta gde prva podintegralna funkcija seče prave x=3 i y=3. Malo sam varao pa sam položaje ove dve tačke sračunao digitronom i ustanovio da je površina trouglića manja od 0.5 * 0.01 *0.01 (oba odsečka su strogo manja od 0.01), tako da je to zaista manje od jednog stotog dela. S druge strane C je još i manje od toga, pa je zbir integrala stvarno manji od 9.0001 čime je dokazan i "desni" deo nejednakosti Međutim, računanje vrednosti odsečaka svodi se tu i tamo na duplo računanje kvadratnog korena što se može i peške, tako da valjda nisam previše "zgrešio". f p.s. Izvinite što nema slike. Još nismo ugradili automatsko slanje priloga u news server. :) [ blaza @ 07.01.2004. 14:26 ] @
[ stalker @ 07.01.2004. 16:36 ] @
[ blaza @ 08.01.2004. 07:58 ] @
Naravno da jesi.
Princip je sledeci: Svaku parcijalnu sumu svesti na oblik k*ATN(...)+m*LN(...) Na kraju se svi LN poniste, i onda preostaje da se dokaze da preostali ATN(...) daju Pi. [ Mihailo Kolundzija @ 08.01.2004. 23:09 ] @
Citat: Ostaje da se pokaze da je C<0.0001, sto nije tesko ako se uoci da je prva podintegralna funkcija konveksna tako da je povrsina C manja od povrsine trougla koga cine tacke (3,3) i mesta gde prva podintegralna funkcija sece prave x=3 i y=3. Malo sam varao pa sam polozaje ove dve tacke sracunao digitronom i ustanovio da je povrsina trouglica manja od 0.5 * 0.01 *0.01 (oba odsecka su strogo manja od 0.01), tako da je to zaista manje od jednog stotog dela. S druge strane C je jos i manje od toga, pa je zbir integrala stvarno manji od 9.0001 cime je dokazan i "desni" deo nejednakosti Medutim, racunanje vrednosti odsecaka svodi se tu i tamo na duplo racunanje kvadratnog korena sto se moze i peske, tako da valjda nisam previse "zgresio". Odlicno obavljen posao. Evo, ako ne zamerate, samo da dodam jednu komplikaciju. Dakle, onaj mali ulubljeni trougao koji ostane se moze naci kao: 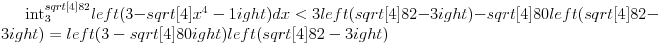 E, sad, posto su oba izraza u zagradama manji od 0.01 (lako se pokaze da je 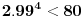 i da je i da je 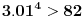 , onda je i njihov , onda je i njihovproizvod manji od 0.0001. Sto se Blazinog zadatka tice, za druge dve sume se dobije "mali milion" integrala, od kojih se mnogi posle sabiranja resenja za obe sume pokrate, tako da se na kraju dobije: 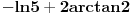 Kad se to sabere sa Brankovim sumama, dobija se 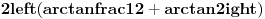 , a to je upravo , a to je upravo 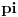 (primenite adicionu formulu za zbir tangensa, nadete inverz od (primenite adicionu formulu za zbir tangensa, nadete inverz oddobijene vrednosti, i na kraju pomnozite sa dva). [ blaza @ 08.01.2004. 23:55 ] @
HeHe. Mihailo je krenuo od kraja, pa je dobio resenje nedostajucih suma. U svakom slucaju, nema smisla izvoditi ovo rucno (kao sto sam ja radio svojevremeno), vec se moze upotrebiti neki od matematickih programa, recimo Mathematica.
[ Mihailo Kolundzija @ 09.01.2004. 02:09 ] @
"blaza" wrote:
> HeHe. Mihailo je krenuo od kraja, pa je dobio resenje nedostajucih suma. U svakom slucaju, nema smisla izvoditi ovo rucno (kao sto sam ja radio svojevremeno), vec se moze upotrebiti neki od matematickih programa, recimo Mathematica. > ---- > Those who can - do. Those who cannot - teach. Those who cannot teach - administrate. > > -- > http://www.elitesecurity.org/poruka/261774 Na žalost, nisi u pravu - baš sam se sit naintegralio. Ako nekog baš zanima kako se neki od dobijenih integrala rešava, neka reklamira. Izvinjenje za one grdobne formule, u svakom slučaju. [ blaza @ 09.01.2004. 15:24 ] @
Dobro, vidim da 6. zadatak nije bio prevelik zalogaj.
Nastavljam sa varijacijama na temu, pa ko nadje vremena, nek se zanima: [ stalker @ 09.01.2004. 17:13 ] @
[ darkosos @ 10.01.2004. 13:24 ] @
[ stalker @ 10.01.2004. 13:32 ] @
Sto se tice onih redova, ja sam zapitkivao slicno pitanje u temi http://www.elitesecurity.org/tema/25477 , tako da ko hoce da radi ovo, neka pogleda Filipov i Srkijev "tutorial", moze puno da pomogne
[ filmil @ 10.01.2004. 20:43 ] @
[ darkosos @ 10.01.2004. 23:11 ] @
Ja volim da stvari idu prirodnim tokom, a provera da je f(x)+f(-x) konstanto nije baš stvar koja prva pada na um. Ali ima nešto drugo što bi moglo da ispravi stvar : "deracionalizacija" onog izraza - povod je to što je originalna funkcija neprekidna pa mora da može i u onakvom obliku da se dobije neprekidna.
Drugi, i možda lepši način je ona stara : 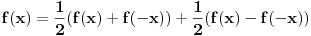 Prvi deo je parna a drugi neparna funkcija. Povod za ovako nečim bi mogao da bude to što je interval integracije simetričan u odnosu na 0, pa možemo pojednostaviti funkciju tako što izbacimo neparan deo. A rastavljanje funkcije na zbir parne i neparne je univerzalno, dakle ništa nismo novo izmislili. Jedino što se ne vidi baš na prvi pogled da će parni deo ispasti tako jednostavno. [ stalker @ 17.01.2004. 00:25 ] @
Ljudi, molim pomoc za ovaj zadatak. Nije bio na olimpijadi, zadao mi ga je ortak koji ide kod Zarka Radosavljevica na matematiku (eto razloga vise da ga uradite:). Ja sam se mucio nedelju dana i stvarno ne znam sta da radim. Dodatni problem je sto nemam nikakvu knjigu ni zbirku iz analize, tako da ne znam ni neke tablicne integrale. Pokusajte, ne verujem da je tesko (i imajte na umu Zarka)
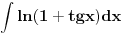 [ filmil @ 17.01.2004. 01:29 ] @
[ stalker @ 17.01.2004. 16:18 ] @
[ petarm @ 04.02.2004. 22:35 ] @
1.) Dokazati cos72°+cos144°= -1/2
Resenje: Polazimo od leve strane I dokazujemo desnu cos72°+cos144°= =cos72°-cos(180°-144°)= ugao od 144° nalazi se u II kvadrantu. =cos72°-cos36°= =cos(54°+18°)-cos(54°-cos18°)= =cos54°cos18°-sin54°sin18°-cos54°cos18°-sin54°sin18°= = -2sin54°sin18°= = -2sin18°cos36°= uglovi 54° 36° su komplementni pa vazi sin54°=cos36° mnozimo dobijeni izraz za cos18°/cos18° = -sin36°cos36°/cos18°= mnozimo dobijeni izraz sa 2/2 = -sin72°/2cos18°= = -cos18/2cos18°= = -1/2 Tako da nam za navedeni dokaz nije potrebno znanje sinusa od 18° Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|