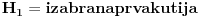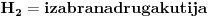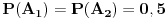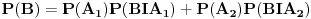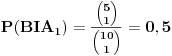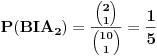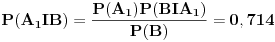[ mungosss @ 14.01.2010. 19:45 ] @
| Imam neki zadatak s kuglicama koji cak ni ne razumem bas najbolje, tj nije mi jasno kad kaze ne zna se koja je od kutija prva a koja druga.Naravno, uvek se trudim da u potpunosti shvatim zadatak iako profesor kaze nema tu neke logike nego covek samo po formuli radi.Mislim nekag mora po formuli al da se razume sta i zbog cega. Kaze ovako: U jednoj kutiji se nalazi 5 crvenih i 5 belih kuglica,a u drugoj 8 crvenih i 2 bele. Ne zna se koja je od te dve kugtije prva a koja druga. Student iz prve kutije izvlaci belu kuglicu i prebacuje je u drugu kutiju. zatim iz druge kutije izvlaci belu kuglicu i prebacuje je u prvu kutiju. Na kraju, student ponovo izvlaci kuglicu iz prve kutije, Ukoliko je ta kuglica bela, kolika je verovatnoca da je ta kutija na pocetku imala po 5 belih i 5 crvenih? |