[ mungosss @ 15.01.2010. 01:22 ] @
integrate (1-2x)/(5-x) dx from x=2 to 3 , uporno dobijam 2 -9(ln2-ln3), medjutim resenje je 2+9(ln2-ln3), ubih se pokusavajuci da nadjem gresku al nikako da uspem .
Kad rastavljam
(1-2x)/(5-x) dobijem 2- 9/(5-x) ,ali to je isto sto i 2+9/x-5 ,ali kad to poste integralim i zamenim granice onda se ne dobije isto, neverovatno .

[Ovu poruku je menjao mungosss dana 15.01.2010. u 02:52 GMT+1]
[ Kal-El @ 15.01.2010. 11:30 ] @
int from 2 to 3 [(1-2x)/(5-x)] dx [ (rastavis na 2-(9/(5-x)) ] = 2*int from 2 to 3 [dx] - 9*int from 2 to 3 [1/(5-x)] = 2(3-2)-9(ln3-ln2)=2-9(ln3-ln2)=2+9(ln2-ln3)
[ mungosss @ 15.01.2010. 12:47 ] @
Hvala, video sam posle, pogresio sam kod smene, treba int 1/5-x, -ln(5-x) :)
[ Cabo @ 15.01.2010. 13:10 ] @
Ček da vidim šta je ovde uopšte bio problem:

.

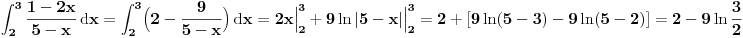
Ako je tako, onda se to dobija kucanjem:

[ tex]\int_2^3\frac{1-2x}{5-x}\,\mathrm{d}x
=\int_2^3\Bigl(2-\frac{9}{5-x}\Bigr)\,\mathrm{d}x
=2x\Big|_2^3+9\ln|5-x|\Big|_2^3
=2+[9\ln (5-3)-9\ln (5-2)]
=2-9\ln\frac{3}{2}[/tex]


[Ovu poruku je menjao Cabo dana 15.01.2010. u 14:34 GMT+1]