preko matematicke indukcije
ako je n>4 tada n|(n-1)! gdje je | oznaka "dijeli" tj (n-1)! je djeljjivo sa n
prvo dokazes da vazi za n=5(jer mora biti vece od 4)
5|24 sto nije tacno

pogledaj jesi li dobro napisao zad

5 nije složen broj...

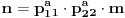
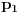
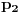
gde su i neka dva prosta faktora sa stepenom većim ili jednakim 1, u rastavljanju na proste čionioce, a ostatak proizvoda.

Sada se verovatno pokaže da su svi oni manji od n-1 za n preko 4, a kako su uzajamno prosti to se nalaze u (n-1)! pa samim tim važi i traženo svojstvo.

_{[Ovu poruku je menjao Goran Rakić dana 23.01.2010. u 04:15 GMT+1]}

5 nije složen broj.

Ako je k>1 i n=p^k stepen prostog broja, onda n|p^k-12p|n! ako je 2p<>p^k-1 i 2p<n. To je ispunjeno za p>2, kao i za p=2, k>3. Za n=8 se neposredno utvdi da 8|8!=2*4*105.

Ako n nije stepen prostog broja, onda je svaki maksimalni stepen prostog broja, koji deli n manji od n, pa se pojavljuje u proizvodu 1*2*...*(n-1)=(n-1)! Pošto su stepeni prostih brojeva uzajamno prosti, njihov proizvod n takođe deli (n-1)!.

Hvala!