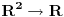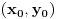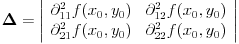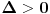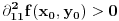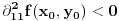[ petarm @ 02.02.2010. 13:25 ] @
|
[ Nedeljko @ 02.02.2010. 13:49 ] @
[ Cabo @ 02.02.2010. 14:03 ] @
Citat: petarm: STA RADIMO AKO JE 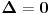 ? ?Ako se dobro sećam Analize 2, onda je kriterijum neodlučiv. Drugim rečima, moraš da radiš na neki drugi način. [ petarm @ 02.02.2010. 14:23 ] @
Citat: Cabo: Ako se dobro sećam Analize 2, onda je kriterijum neodlučiv. Drugim rečima, moraš da radiš na neki drugi način. Na koji npr.? [ Cabo @ 02.02.2010. 14:30 ] @
Pa gledaj logično. Kada je nešto ekstremum (recimo maksimum)? Maksimum imaš ako imaš „džombu“, što znači da su sve vrednosti funkcije u okolini te tačke manje od vrednosti funkcije u samoj tački. E, sad, samo to zapišeš i...
U suštini, svodi se na baratanje nejednakostima i razlikama. I izvodi su količnici razlika, samo malo jednostavniji za rad (čitaj: imaju tablice izvoda). DODATAK: Mislim da ako se radi baš o „ploči“, onda nema ekstremuma. [ Nedeljko @ 02.02.2010. 20:27 ] @
Primeti da je
 funkcija, koja je u slučaju neprekidnosti parcijalnih izvoda neprekidna. Ako je funkcija, koja je u slučaju neprekidnosti parcijalnih izvoda neprekidna. Ako je 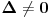 u razmatranoj tački, onda je to slučaj i u njenoj okolini, pa je zato i kriterijum takav. U suprotnom moraš da razmatraš u razmatranoj tački, onda je to slučaj i u njenoj okolini, pa je zato i kriterijum takav. U suprotnom moraš da razmatraš  u okolini razmatrane tačke. u okolini razmatrane tačke.Drugi način je rešavanje diferencijalne jednačine 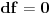 , odnosno , odnosno 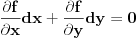 . Ako dobiješ da je . Ako dobiješ da je 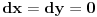 onda imaš ekstremum, u protivnom ne. onda imaš ekstremum, u protivnom ne.[ petarm @ 03.02.2010. 08:27 ] @
Citat: Nedeljko: Primeti da je  funkcija, koja je u slučaju neprekidnosti parcijalnih izvoda neprekidna. Ako je funkcija, koja je u slučaju neprekidnosti parcijalnih izvoda neprekidna. Ako je 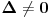 u razmatranoj tački, onda je to slučaj i u njenoj okolini, pa je zato i kriterijum takav. U suprotnom moraš da razmatraš u razmatranoj tački, onda je to slučaj i u njenoj okolini, pa je zato i kriterijum takav. U suprotnom moraš da razmatraš  u okolini razmatrane tačke. u okolini razmatrane tačke.Drugi način je rešavanje diferencijalne jednačine 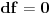 , odnosno , odnosno 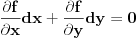 . Ako dobiješ da je . Ako dobiješ da je 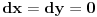 onda imaš ekstremum, u protivnom ne. onda imaš ekstremum, u protivnom ne.Hvala na odgovoru! [ Fitopatolog @ 03.02.2010. 08:27 ] @
Citat: Moguće je da funkcija u taj tački ima tzv. "sedlo", ali to i ne mora biti slučaj. Razvij funkciju u Tejlorov red (ako imaš vremena) pa vidi šta je sa trećim članom (onim uz 1/3!). Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|