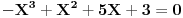|
|
[ dejan s @ 02.02.2010. 18:01 ] @
|
|
Kako bi se npr, ovaj polinom rastavio na činioce pomoću hornerove šeme
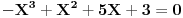
Evo, znači znam početak, gore pišem koeficijente
..|-1| 1| 5| 3|
--------------
L| A| B| C| D|
P| E| F| G| H|
Eto, znači to znam, ali koji su mi ovo brojevi L i P? šta tu treba da upišem?
I otprilike znam postupak kako se računa A B C i D, bilo bi ovako valjda:
A= L * (-1)
B= 1 + L * A
C= 5 + L * B
D= 3 + L * C
Jel tako? ili sam ja tu nesto zeznuo? I sta dalje? Sta sam ja ustvari dobio iz te tabele? Eto jos konkretnijeg pitanja....
-----------------
Citat: Morala je prethodno biti rađena na predavanjima (ili na vežbama)
Sve je to lepo, ali ja nisam pohađao baš ta predavanja i vežbe kada su se obrađivali polinomi :/
Bojan Basic - daj čoveče, ja sam samo pitao kako se radi taj zadatak tj. kako se radi hornerova šema, to NE ZNAM! I DON'T KNOW! Ja sam baš zato i pitao ako može neko da mi uradi ovaj zadatak, tako bih provalio postupak za 5 minuta. A da sam uzmem da provaljujem, otići će mi mnogo više vremena, a ispit imam za dva dana.... Ja nisam postavio pitanje da bi mi neko pričao kako treba sam lepo da se mučim i provaljujem stvari (sve to stoji, naravno ništa protiv toga), nego sam postavio konkretno pitanje - tražim konkretan odgovor, bez filozofiranja moliću. Hvala najlepše. A ti sad kako hoćeš, obriši mi temu, radi šta želiš....
PS morao sam da spamujem i otvorim jos jednu temu, kad si mi proslu zakljucao.... |
[ Janinka @ 02.02.2010. 19:51 ] @
Koliko se ja secam,u prvoj koloni odmah ispod vodeceg kojeficijenta,u slucaju -1,taj se isti prepise.Sledeca kolona(i svaka naredna) se racuna tako sto se mnozi potencijalna nula polinoma(a kandidati za potencijalne nule su faktori slobodnog clana datog polinoma,u slucaju -1,1,-3 i 3) pomnozi sa prethodnom kolonom i doda broj iznad kolone koja se racuna.Ukoliko je poslednja kolona nula,onda je potencijalna nula u stvari nula polinoma.
Znaci,u prvom redu imas redom -1, 1 , 5, 3 I ako je potencijalna nula -1 dobijas redom
-1, (-1)(-1)+1=2 , 2(-1)+5=3, 3(-1)+3=0 Znaci,-1 je nula polinoma.Zato sada radis drugu kolonu sa pot.nulom 1 -1 1(-1)+2=1 , 1*1+3=4 , 1*4+0=4 Znaci 1 nije nula,pa se zadnji red ne racuna,t.j.racuna se prethodni -1 2 3 0 (Ovo mozes rastaviti na cinioce kao kv.trinom,ali moze i HS,pot.nula je 3 -1 3(-1)+2=-1 , 3(-1)+3=0 Znaci i 3 je nula,ostaje linearni binom -x-1
Konacno se dobija (x+1)(x-3)(-x-1)=-(x+1)^2*(x-3)
[ dejan s @ 02.02.2010. 21:08 ] @
Jao Janinka, spasila si mi život, nemaš pojma koliko si mi pomogla! Hvala ti puuuuuuuuno :)))
Ali nije mi jasno "linearni binom -x-1". Odakle si to izvukla, kako si došla do toga :O ? Možda je glupo pitanje, ali ja se takoreći prvi put susrećem sa polinomima, pa mi još svi pojmovi nisu jasni, malo se gubim....
I samo još ovo, kažeš "Ovo mozes rastaviti na cinioce kao kv.trinom". Ček polako. Kako bi izgledao taj kvadratni trinom?
Da li to što je nula polinoma -1 znači da bi ovaj polinom sa početka bio deljiv sa (x+1) ? Pa onda podelim početni polinom sa (x+1) i dobijem taj kvadratni trinom? Ili postoji neki kraći način?
EDIT: Aaa mislim da sam skontao, ne mora da se deli, nego mi je zapravo ovaj ceo red (-1 2 3 0) predstavlja koeficijente ahaaaaa :) Pa mi je sledeći red (-1 -1 0 0) I odatle se vidi da je ovo -x -1 :)))
Ok, to je jasno ;) Hvala još jednom ;)
Jbg, imao sam profesora u srednjoj koj je dolazio pijan na časove, tako da pojma ništa nemam i sad ne znam šta ću da radim...
[Ovu poruku je menjao dejan s dana 02.02.2010. u 22:31 GMT+1]
[ petarm @ 03.02.2010. 08:25 ] @
[ Janinka @ 03.02.2010. 19:16 ] @
Citat: Ali nije mi jasno "linearni binom -x-1".
Pa dobija se polinom prvog stepena(linearni) sa kojeficijentima -1 i -1(to se vidi iz zadnjeg reda),t.j.-x-1.
Citat: I samo još ovo, kažeš "Ovo mozes rastaviti na cinioce kao kv.trinom". Ček polako. Kako bi izgledao taj kvadratni trinom?
Od toga sto se dobija red sa kojeficijentima -1,2,3 to su kojeficijenti kvadratnog trinoma -x^2+2x+3,koji pomocu formule mozes razloziti na cinioce,ali ako se trazi potpuna primena HS,mora se ici do kraja
Citat: Da li to što je nula polinoma -1 znači da bi ovaj polinom sa početka bio deljiv sa (x+1) ? Pa onda podelim početni polinom sa (x+1) i dobijem taj kvadratni trinom? Ili postoji neki kraći način?
Moglo se odmah posle prvog delenja sa binomom x+1 proveriti da li je -1 dupla nula,dobili bi se drugi kojeficijenti,ali opet bi se dobio isti rezultat.
Citat: Jao Janinka, spasila si mi život, nemaš pojma koliko si mi pomogla! Hvala ti puuuuuuuuno :)))
Nema na cemu,drago mi je ako sam pomogla...
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|