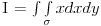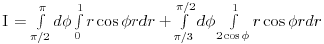[ del-boy @ 08.02.2010. 19:34 ] @
|
[ Cabo @ 08.02.2010. 20:10 ] @
Pa, prosto. Uvek ćeš imati neke jednačine. Samo treba da provališ iz njih koje su granice za promenljive
 , ,  , ,  , itd. To se lakše radi preko polarnih koordinata. To je sva mudrost — lakše, preko polarnih kordinata. U određenim slučajevima. , itd. To se lakše radi preko polarnih koordinata. To je sva mudrost — lakše, preko polarnih kordinata. U određenim slučajevima.Ako oblasti izgledaju previše komplikovano — iscepkaj ih na jednostavnije. Dvojni i trojni integrali su najlakši. Površinski su neznatno komplikovaniji, ali prava težina u Analizi 2 su parametarski integrali. Kad njih savladaš, svi ostali su ti teški koliko i 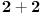 . .[ del-boy @ 09.02.2010. 00:19 ] @
Da li to znači da ne postoji neko pravilo, nego je svaki zadatak za sebe?
U ovom konkretnom slučaju, kad se računa površina dela na pozitivnoj strani  ose, donja granica je ose, donja granica je 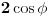 . To sam nema šanse da bih pretpostavio. Ovako kad vidim, možda nekako mogu intuitivno da pretpostavim zašto je to tako, ali ne i da objasnim. Zato me zanima da mi neko objasni zašto je u ovom slučaju ovakva situacija, a ako već jeste svaki zadatak za sebe, bez nekog pravila, pitaću ponovo ako naletim na nešto što ne mogu da skontam :) . To sam nema šanse da bih pretpostavio. Ovako kad vidim, možda nekako mogu intuitivno da pretpostavim zašto je to tako, ali ne i da objasnim. Zato me zanima da mi neko objasni zašto je u ovom slučaju ovakva situacija, a ako već jeste svaki zadatak za sebe, bez nekog pravila, pitaću ponovo ako naletim na nešto što ne mogu da skontam :)[ Nedeljko @ 09.02.2010. 08:40 ] @
[ Cabo @ 09.02.2010. 13:21 ] @
Citat: del-boy: donja granica je 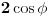 . To sam nema šanse da bih pretpostavio. . To sam nema šanse da bih pretpostavio.Dovijaš se kako znaš. Dakle, vidiš da treba ići od kruga sa centrom u 1 (ako ne grešim), pa gledaš kako bi predstavio to u polarnim koordinatama. A kada jednom primeniš polarne koordinate, ne traži neki smisao (pod tim mislim na ono „kako bi se do toga došlo 's neba pa u rebra', da nismo krenuli od  i i  “). “).[ del-boy @ 09.02.2010. 17:58 ] @
Toga sam se i bojao :)
Hvala u svakom slučaju... [ miki069 @ 09.02.2010. 19:07 ] @
Nemoj toga da se bojiš.
Kako bi izgledala slika da je u drugom integralu bilo r na intervalu od 0 do 1? Nacrtaj tu sliku pa će onda biti jasnije zašto r ide od 2*cos(fi) do 1. Savet: uzmi Apsena 3. Uz nedostatke koje knjiga ima (Nedeljko ih već navodio detaljno), objašnjeno je do detalja kako se određuju granice. Sve je lepo ilustrovano. Za tehničke fakultete više nego dovoljno. [ Cabo @ 09.02.2010. 20:20 ] @
Pa nema šta, cilj zadataka sa dvojnim i trojnim integralima ti je da dobiješ neku konstantu (uglavnom...), a ne da razmatraš šta je šta i kako izgleda. Dakle, račun, račun, i — rezultat.
Čak sam sablažnjavao neke kolege izjavom da slika uopšte nije potrebna, samo gledaš formule. [ del-boy @ 09.02.2010. 22:14 ] @
Citat: miki069: Nemoj toga da se bojiš. Kako bi izgledala slika da je u drugom integralu bilo r na intervalu od 0 do 1? Nacrtaj tu sliku pa će onda biti jasnije zašto r ide od 2*cos(fi) do 1. Savet: uzmi Apsena 3. Uz nedostatke koje knjiga ima (Nedeljko ih već navodio detaljno), objašnjeno je do detalja kako se određuju granice. Sve je lepo ilustrovano. Za tehničke fakultete više nego dovoljno. Da, jasnije je kad postavim  umesto umesto 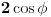 . . Mnogo pomaže kad probaš integral tipa 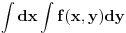 da pretvoriš u da pretvoriš u 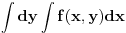 . Uradio sam to na par primera i sad dosta bolje razumem načine dobijanja granica... . Uradio sam to na par primera i sad dosta bolje razumem načine dobijanja granica... [ zzzz @ 09.02.2010. 23:27 ] @
Ja nisam zadovoljan kako su ti pomagali Nedeljko,Savo i Miki.
Uglavnom su vrlo uspješni ali vidim da ih ne kužiš jer su površni. Da probam i ja pompći: 1)Uvijek granice određuj uz pomoć geometrijske slike! 2)Ako granice nisu konstanta (a to je u ovom primjeru slučaj!), probaj na osnovu slike napraviti funkcijonalnu zavisnost te granice o narednoj varijabli.(r=f(fi) Sad bih ja mogao napraviti slikicu pa da ti bude odmah sve jasno,ali radije neću. Probaću pričom dočarati pa sam crtaj. Zamisli da da na onom tvom crtežu neka poluprava sa centrom u ishodištu rotira kontra kazaljki sata.I onda na 60 stepeni počne kačiti onu zatamnjenu ravan.I za svaki naredni djelić ugla zatamni dio one osjenčene površine.U opštem slučaju udaljenost vanjske ivice od centra je jedan (konstanta).To ti je vanjska granica integracije za r.A unutrašnja granica nije konstanta.Nekako ide ka centru rotacije zato što slijedi onu drugu kružnicu,jel tako?(A za ugao granice su ti od 60 do 90 stepeni.) Ajmo naći udaljenost tačke presjeka (poluprave i one druge kružnice) od centra rotacije u ovisnosti od fi. (A to nam je ta donja granica integracije i treba nam) Za rješavanja ovog problema obavezno treba znati da je periferni ugao u kružnici duplo manji od centralnog i da je za slučaj da je centralni ugao 180 stepeni,onaj periferni jednak 90 (pravi). Odavde slijedi da je ona donja granica zapravo manja kateta pravouglog trokuta kome hipotuneza leži na x osi i ima dužinu 2,a nassuprot nje je ugao jednak fi.Jel tako?Pa je onda ta donja granica jednaka 2sin(fi). A ne 2cos(fi)!,ako nisam gdje pogriješio. [ miki069 @ 09.02.2010. 23:52 ] @
Milane baš lepo dočarano.
Ipak je 2*cos(fi) [ zzzz @ 10.02.2010. 00:04 ] @
Citat: miki069: Milane baš lepo dočarano. Ipak je 2*cos(fi) Idem iz kafane pun piva.U pravu si jer ono nasuprot nije bio ugao fi već 90-fi.Sve vidim duplo šta ćeš. [ Cabo @ 10.02.2010. 14:47 ] @
Ljuta >>> pivo.
Bolje je biti površno tačan. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|