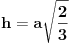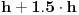[ pailhead @ 13.02.2010. 17:47 ] @
|
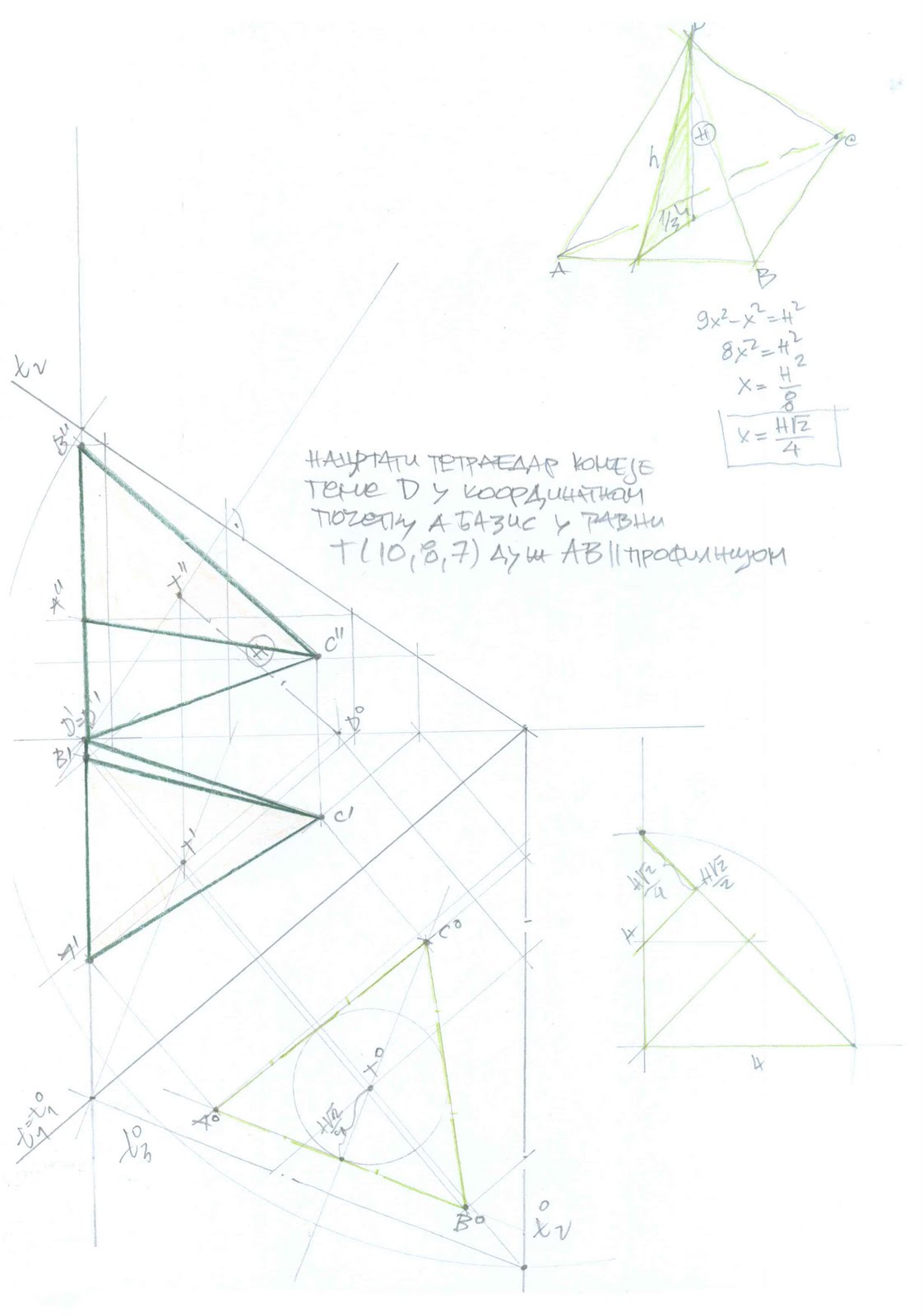
| Jel moguce pronaci stranicu a nekog tetraedra ako je zadata visina tetraedra, uz pomoc nacrtne geometrije?
Ako sam dobro odradio matematiku, dobio sam neki koren iz 15 u odnosu a i h.
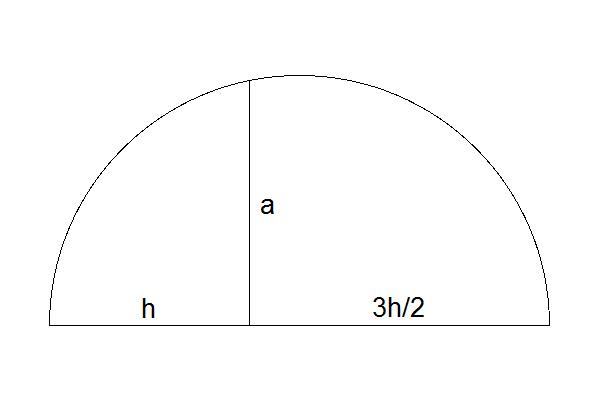
h se lako dobija sa a, tako sto se konstruise jednakostranicni trougao, zatim se povuce pomocna linija iz tezista trougla paralelna sa jednom od stranica tog trougla, i onda se iz naspramnog temena prenese a na tu pomocnu liniju. Rezultat je trougao koji ima a kao hipotenuzu, h kao jednu katetu, i 2/3 h jednakostranicnog trougla kao drugu katetu.
Medjutim, nije mi jasno da li je moguce geometrijski obrnuti redosled? |
[ Nedeljko @ 13.02.2010. 18:03 ] @
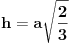 . [ Cabo @ 13.02.2010. 19:23 ] @
Na trenutak sam pomislio da ovo ima nekakve veze sa Nacrtnom geometrijom. Taj trenutak je potrajao dok nisam otvorio temu.
-_______-
[ galet@world @ 13.02.2010. 20:41 ] @
Citat: pailhead: Jel moguce pronaci stranicu a nekog tetraedra ako je zadata visina tetraedra, uz pomoc nacrtne geometrije?
Moguće je uz pomoć konstrukcije sličnih trouglova. Evo: [ galet@world @ 14.02.2010. 07:08 ] @
U prethodnoj poruci nisam uspeo da nacrtam trougao ABC tako da bude jednakostraničan,
pa konstrukcija, iako principijelno ispravna, izgleda pogrešno. Evo tačnije konstrukcije:
[ Nedeljko @ 14.02.2010. 08:58 ] @
Ima i lakših načina.
 [ galet@world @ 14.02.2010. 11:48 ] @
Ima. Na primer, potrebno je izračunati h/4 i onda se konstruiše pravougli
trougao kojem je hipotenuza 5h/4 i jedna kateta je h/4 i gotovo, ali zašto
da to radimo kad možemo i tu drugu katetu izračunati?
Ovo je mešavina izračunavanja i konstruisanja.
Radi se o nacrtnoj geometriji, odnosno planimetriji i konstruisanju
geometrijskih veličina bez izračunavanja. [ zzzz @ 14.02.2010. 12:14 ] @
Na primer, potrebno je izračunati h/4 i onda...
Ne treba algebarski ništa raditi jer je u geometriji polovljenje,četvrtanje
itd ,a pomoću šestara i lenjira,osnovna radnja.
[ zzzz @ 14.02.2010. 14:41 ] @
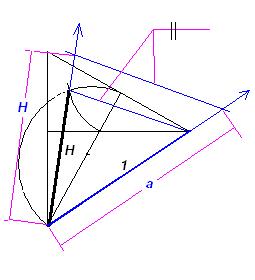
Evo jedne konstrukcije gdje izbjegavamo Pitagoru.ali
ima malo Talesa (može se i taj teorem izbjeći,ali zašto.)
-Nacrtam istostraničan trokut stranice 1 i dvije visine.
-Nad jednom od visina nacrtam polukružnicu.
-Povučem luk iz sjecišta visina do polukružnice,a centar
luka je podnožje visine nad kojom je polukružnica.
-Udaljenost vrha ove visine i sjecišta luka sa polukružnicom
je visina tetraedra.
Ako imamo zadanu visinu (ili stranicu) tetraedra onda stranicu
(ili visinu) dobijemo iz sličnosti trokutova kao na slici.
 [ galet@world @ 14.02.2010. 15:36 ] @
Citat: zzzz:Ne treba algebarski ništa raditi...
Tačno. To sam i ja rekao: Citat: galet@world:
Radi se o nacrtnoj geometriji, odnosno planimetriji i konstruisanju
geometrijskih veličina bez izračunavanja. [ Nedeljko @ 14.02.2010. 21:48 ] @
Pa, ja ništa nisam algebarski računao. 3h/2 se vrlo lako konstruiše polazeći od h. Ne znam čemu onda ovaj komentar
Citat: galet@world: Ima. Na primer, potrebno je izračunati h/4 i onda se konstruiše pravougli
trougao kojem je hipotenuza 5h/4 i jedna kateta je h/4 i gotovo, ali zašto
da to radimo kad možemo i tu drugu katetu izračunati?
Ovo je mešavina izračunavanja i konstruisanja.
Radi se o nacrtnoj geometriji, odnosno planimetriji i konstruisanju
geometrijskih veličina bez izračunavanja. [ zzzz @ 14.02.2010. 22:33 ] @
Citat: Nedeljko: Pa, ja ništa nisam algebarski računao. 3h/2 se vrlo lako konstruiše polazeći od h. Ne znam čemu onda ovaj komentar
Ali za konstrukciju dijametra si koristio 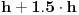 ,a to si isčupao iz 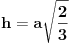
što se dobija algebarski pomoću pitagore. [ Nedeljko @ 15.02.2010. 05:57 ] @
Dokazuje se da je to to preko Pitagore, ali dokazi se i nemogu iyvoditi lenjirom i šestarom, već rasuđivanjem.
Konstrukcija je lenjirom i šestarom i dobija se ono što treba. To i jeste zadatak geometrijskih konstrukcija.
[ galet@world @ 15.02.2010. 07:43 ] @
Citat: Nedeljko: Dokazuje se da je to to preko Pitagore, ali dokazi se i nemogu iyvoditi lenjirom i šestarom, već rasuđivanjem.
Tako je, ali se traži da se geometrijska konstrukcija izvede (kompletno a ne delimično)
lenjirom i šestarom, a ispravnost konstrukcije se dokazuje rasuđivanjem odnosno računski
koristeći već dokazane teoreme. [ Nedeljko @ 15.02.2010. 15:49 ] @
Koji je deo konstrukcije sporan?
Neka je data duz AB duzine h.
1. Konstruisati pravu p kroz tacke A i B.
2. Konstruisati krug k1 sa centrom B, koji prolazi kroz tacku A.
3. Konstruisati presecnu tacku C prave p i kruga k1, koja se razlikuje od tacke A.
4. Konstruisati krug k2 sa centrom C, kroz tacku B.
5. Konstruisati presecnu tacku D kruga k2 i prave p, koja se razlikuje od tacke B.
6. Konstruisati krug k3 sa centrom C kroz tacku D.
7. Konstruisati krug k4 sa centrom D kroz tacku C.
8. Konstruisati presecne tacke M1 i M2 krigova k3 i k4.
9. Konstruisati pravu q kroz tacke M1 i M2.
10. Konstruisati presecnu tacku E pravih p i q.
11. Konstruisati krug k5 sa centrom A kroz tacku E.
12. Konstruisati krug k6 sa centrom E kroz tacku A.
13. Konstruisati presecne tacke N1 i N2 krugova k5 i k6.
14. Konstruisati pravu r kroz tacke N1 i N2.
15. Konstruisati presecnu tacku O pravih p i r.
16. Konstruisati krug k sa centrom O kroz tacku A.
17. Konstruisati krug k7 sa centrom A kroz tacku C.
18. Konstruisati krug k8 sa centrom C kroz tacku A.
19. Konstruisati presecne tacke P1 i P2 krugova k7 i k8.
20. Konstruisati pravu s kroz tacke P1 i P2.
21. Konstruisati presecne tacke Q1 i Q2 prave s i kruga k.
Bilo koja od duzi BQ1 i BQ2 ima trazenu duzinu a.
Ovo je najpostupnije za one koji ne znaju da konstruisu ni srediste duzi. Oslanja se samo na sledecih 5 osnovnih konstrukcija.
1. Konstrukcija prave kroz dve tacke.
2. Konstrukcija kruga sa datim centrom kroz datu tacku.
3. Konstrukcija presecne tacke dveju pravih.
4. Konstrukcija presecnih tacaka prave i kruga.
5. Konstrukcija presecnih tacaka dvaju krugova.
Za 1 je potrebanm lenjir, za 2 sestar, a za 3, 4 i 5 samo olovka. Pritom se smatra da je duz data svojim klrajevima.
[ galet@world @ 16.02.2010. 06:25 ] @
Citat: Nedeljko: Koji je deo konstrukcije sporan?
Ni jedan, ali je sporan početak jer je bio računski.
Zadaci se postavljaju uz uslov da se konstruišu traženi geometrijski
elementi bez prethodne računske modifikacije zadatih elemenata
ili
da li je moguće konstruisati tražene elemente bez te modifikacije. [ Nedeljko @ 16.02.2010. 08:44 ] @
Ovde neko očigledno ne zna šta su geometrijske konstrukcije i šta je njihov zadatak.
[ galet@world @ 16.02.2010. 11:02 ] @
Dvojica znaju, a jedan ne zna.
[ Nedeljko @ 16.02.2010. 12:38 ] @
OK, prosvetli me!
[ Cabo @ 16.02.2010. 13:38 ] @
„Konstruisati“ je pojam koji nema dve blage veze sa papirom, olovkom, niti šestarom.
Ono na šta se misli kada se kaže „konstrukcija šestarom“ jeste očuvanje dužina.
Galet bi pao na Osnovama geometrije ko dulek.  [ Nedeljko @ 16.02.2010. 14:04 ] @
U konstrukciji lenjirom i šestarom se podrazumeva da su na početku zadate bar dve tačke i da od onoga što je dato treba dobiti ono što se traži konačnom primenom ovih pet koraka
Citat: Nedeljko:
1. Konstrukcija prave kroz dve tacke.
2. Konstrukcija kruga sa datim centrom kroz datu tacku.
3. Konstrukcija presecne tacke dveju pravih.
4. Konstrukcija presecnih tacaka prave i kruga.
5. Konstrukcija presecnih tacaka dvaju krugova.
U našem zadatku je data duž podudarna visini tetraedra, a traži se duž podudarna ivici tetraedra. [ galet@world @ 16.02.2010. 14:47 ] @
Što da ne!
Citat: Riješiti konstruktivni zadatak znači na osnovi onoga što je u njemu dano konstruirati figuru koja se traži, upotrebljavajući pritom samo šestar i ravnalo s jednim bridom. Pri rješavanju konstruktivnih zadaća jednobridnim ravnalom i šestarom koristimo se raznim metodama. Neke od najčešće korištenih metoda geometrijskog konstruiranja su metoda presjeka skupova točaka odnosno metoda geometrijskih mjesta točaka, metoda pomoćnih likova i metoda geometrijskih transformacija. O tim metodama više možete doznati u [1]. Međutim ponekad se dogodi da niti jednom od spomenutih
metoda geometrijskog konstruiranja,
bez obzira koliko se trudili, ne možemo riješiti neki konstruktivni zadatak. Tada možemo pokušati naš konstruktivni zadatak riješiti primjenom
algebarske metode rješavanja konstruktivnih zadaća.
Ne mogu uvek da te "prosvetljujem". Moraš malo i sam da poradiš na tom.
Citat: Cabo:Galet bi pao na Osnovama geometrije ko dulek.
Ni slučajno, ali onaj ko smatra da nacrtna geometrija isključuje planimetriju je već pao kao, na primer, ovaj junak dole:
Citat: Na trenutak sam pomislio da ovo ima nekakve veze sa Nacrtnom geometrijom. Taj trenutak je potrajao dok nisam otvorio temu. [ Nedeljko @ 16.02.2010. 15:46 ] @
Ono što sam napisao je precizna definicija koju sam učio na fakultetu. No, i po ovome što si citirao sam opet ja u pravu, jer se opet radi o metodi rešavanja konstruktivnih zadataka. Šta ti vrede citati kad ih ne razumeš.
Algebarski pristup je naročito značajan kada se dokazuje da neka konstrukcija nije moguća lenjirom i šestarom (podela proizvoljnog ugla na n delova, gde je n fiksirani prirodan broj koji nije stepen dvojke; duplikacija kocke, kvadratura kruga itd.). Ti problemi su rešeni tako što je algebarskim metodama dokazano da tražene konstrukcije ne postoje.
OK, nakon što si me prosvetio, evo tebi jednog iscrpnog članka da se prosvećuješ.
http://en.wikipedia.org/wiki/C...and_straightedge_constructions[ galet@world @ 16.02.2010. 19:02 ] @
Citat: Nedeljko: Ono što sam napisao je precizna definicija koju sam učio na fakultetu. No, i po ovome što si citirao sam opet ja u pravu, jer se opet radi o metodi rešavanja konstruktivnih zadataka.
Kojoj? [ Nedeljko @ 16.02.2010. 21:00 ] @
Onoj što si je citirao.
[ miki069 @ 17.02.2010. 01:34 ] @
Konstrukcija se sastoji od:
1. Analize
2. Opisa konstrukcije
3. DOKAZA KONSTRUKCIJE
4. Konstrukcije i
5. Diskusije
U analizi, a pogotovo u dokazu, sme se koristiti sve osim Furijeovih redova i Laplasove transformacije.
Sama konstrukcija bez dokaza vredi nula.
Nedeljkovo rešenje je kompletno sa sve diskusijom.
Elegantnije 100 puta od ostala dva, ako su ta druga dva uopšte ispravna.
Ostala dva rešenja su čist fenseraj.
Možda su i ispravna, ali nema DOKAZA, pa vrede nula.
Tako bilo, davno, kad sam ja učio geometriju
Valjda se ništa nije promenilo.
Inače hipotenzina visina koju je Nedeljko koristio rešava ključne delove mnogo težih zadataka.
Odatle je postavljač zadatka mogao nešta da nauči.
[ galet@world @ 17.02.2010. 04:17 ] @
Konačno si priznao. To si mogao i ranije da uradiš a ne da kažeš
Citat: Pa, ja ništa nisam algebarski računao...
jer to nije tačno što ti je zzzz svojom porukom od 14. 2. (u 23:32) i pokazao. [ galet@world @ 17.02.2010. 08:46 ] @
Dobro Nedeljko da batalimo ovo prepucavanje - obećavam da to više neću
činiti pa makar bio izazvan - nego da pokušamo rešiti bilo kojim metodom ovaj
zadatak:
Nacrtan je prav ugao i unutar njega data je jedna tačka i data je jedna duž
koja treba da prođe kroz tu tačku i sa krakovima pravog ugla da čini
pravougli trougao. Duž nije prekratka pa može da dodiruje oba kraka
nacrtanog pravog ugla.
Ja sam pokušao i nisam uspeo, a zadatak je naizgled vrlo jednostavan.
Ovaj zadatak sam postavio još 30. 10. 2007. i niko ga nije ni pokušao
rešiti.
[ mokelet @ 17.02.2010. 10:46 ] @
Citat: galet@world:
Nacrtan je prav ugao i unutar njega data je jedna tačka i data je jedna duž
koja treba da prođe kroz tu tačku i sa krakovima pravog ugla da čini
pravougli trougao. Duž nije prekratka pa može da dodiruje oba kraka
nacrtanog pravog ugla.
Konstruišeš kružnicu sa centrom u datoj tački i poluprečnikom jednakim polovini date duži.
Presečne tačke krakova pravog ugla i kružnice biće preostala dva temena traženog pravouglog trougla. [ Nedeljko @ 17.02.2010. 10:46 ] @
Dane, biće da si ti priznao da sam koristio legitimnun metodu rešavanja konstruktivnih zadataka.
Ovaj novi zadatak je najverovatnije nerešiv lenjirom i šestarom, ali nisam još to dokazao. Sada nemam vremena.
mokolet, tako ćeš dobiti izlomljenu a ne pravu duž koja ispunjava uslove, ako krug uopšte preseče oba kraka pravog ugla.
[ mokelet @ 17.02.2010. 11:00 ] @
Citat: Nedeljko:
mokolet, tako ćeš dobiti izlomljenu a ne pravu duž koja ispunjava uslove, ako krug uopšte preseče oba kraka pravog ugla.
U pravu si, na brzinu sam pročitao zadatak. [ galet@world @ 17.02.2010. 14:03 ] @
Citat: Nedeljko: Dane, biće da si ti priznao da sam koristio legitimnun metodu rešavanja konstruktivnih zadataka.
Pa naravno Nedeljko, to nije sporno - ja ne tvrdim da algebarski metod nije legitiman -
samo sam tvrdio da to nije geometrijski metod. [ galet@world @ 17.02.2010. 14:51 ] @
Citat: Nedeljko:
Ovaj novi zadatak je najverovatnije nerešiv lenjirom i šestarom, ali nisam još to dokazao.
Pokušavao sam i algebarski, ali dobijem neku jednačinu trećeg stepena, a očigledno
je da postoje dva simetrična rešenja u odnosu na simetralu pravog ugla.
(Geometrijski sam to nekako rešio, ali nažalost, uz nedopustivu primenu lenjira i šestara.)
[Ovu poruku je menjao galet@world dana 17.02.2010. u 16:21 GMT+1][ Nedeljko @ 17.02.2010. 16:15 ] @
Da, reč je o zadatku koji je nerešiv lenirom i šestarom. Znam tačno o kakvoj upotrebi lenjira pričaš. To se zove lenjir sa dva zareza. Sa takvom spravom može.
[ galet@world @ 17.02.2010. 18:42 ] @
Citat: Nedeljko: Da, reč je o zadatku koji je nerešiv lenirom i šestarom. Znam tačno o kakvoj upotrebi lenjira pričaš. To se zove lenjir sa dva zareza. Sa takvom spravom može.
Tačno. To je onda sprava. I šta je još gore - šestar ne vrši nikakvu svoju funkciju već
ubodeni kraj ima ulogu kliznog graničnika.
Ali šta da radimo? Zadatak je nesumnjivo rešiv. To upravo pokazuje taj nedozvoljeni lenjir
i nefunkcionalna upotreba šestara. [ Nedeljko @ 17.02.2010. 20:37 ] @
Nerešiv je lenjirom i šestarom, a lenjirom sa dva zareza je sasvim rešiv. To je druga sprava, pa samim tim i drugi zadatak..
[ galet@world @ 18.02.2010. 09:33 ] @
Citat: Nedeljko: Nerešiv je lenjirom i šestarom, ...
Ali kako je uopšte rešiv?
Ako sa x označim jednu katetu onda u opštem slučaju dobijam jednačinu četvrtog stepena
po x i to ovakvu:
ax 4 + bx 3 + cx 2 + dx + k = 0 [ Nedeljko @ 18.02.2010. 10:30 ] @
Pa, rešiv je lenjirom sa dva zareza, jer je to moćnija sprava od običnog lenjira.
Lenjir sa dva zareza uz šestar može da rešava sve jednačine do četvrtog stepena.
[ galet@world @ 18.02.2010. 13:02 ] @
Citat: Nedeljko: Lenjir sa dva zareza uz šestar može da rešava sve jednačine do četvrtog stepena.
Dobro, ali možemo li izračunati tačnu dužinu kateta? [ Nedeljko @ 18.02.2010. 16:24 ] @
Naravno da možemo. Sve algebarske jednačine do stepena 4 su rešive preko radikala.
[ Nedeljko @ 19.02.2010. 00:14 ] @
Citat: galet@world: Pa naravno Nedeljko, to nije sporno - ja ne tvrdim da algebarski metod nije legitiman -
samo sam tvrdio da to nije geometrijski metod.
Poslednji put, konstrukcija je ono što sam naveo u poruci
http://www.elitesecurity.org/p2522653
Dakle, onaj 21. korak. Račun koji pominješ nije deo konstrukcije nego analize, a oba su sastavni delovi rešavanja konstruktivnog zadatka. [ galet@world @ 19.02.2010. 08:24 ] @
Citat: Nedeljko: Račun koji pominješ nije deo konstrukcije nego analize, a oba su sastavni delovi rešavanja konstruktivnog zadatka.
Opet se slažem i dodajem da se takav metod rešavanja konstruktivnih zadataka zove algebarski metod. [ Nedeljko @ 19.02.2010. 11:12 ] @
I u čemu je onda problem?
[ galet@world @ 19.02.2010. 16:53 ] @
Citat: Nedeljko: I u čemu je onda problem?
Pa nema problema. Ja tvrdim da algebarski metod nije geometrijski metod,
a ti tvrdiš da je algebarski metod legitiman i sve je u redu. Jedini problem
je u tome što ti tvrdiš da ništa nisi računao, pa bi iz toga sledilo da si i ti
rešio problem geometrijskim metodom. [ Nedeljko @ 21.02.2010. 10:40 ] @
Prvo siu napravio problem od mog rešenja, a sad nema nikakvih problema.
[ galet@world @ 21.02.2010. 13:04 ] @
Citat: Nedeljko: Prvo siu napravio problem od mog rešenja, a sad nema nikakvih problema.
Nisam napravio problem od tvog rešenja jer je ispravno.
Samo pitam - kojim metodom si došao do tvog rešenja? [ Nedeljko @ 21.02.2010. 13:20 ] @
Citat: galet@world: Tako je, ali se traži da se geometrijska konstrukcija izvede (kompletno a ne delimično) lenjirom i šestarom, a ispravnost konstrukcije se dokazuje rasuđivanjem odnosno računski koristeći već dokazane teoreme.
Odavde ispada da nisam uradio ono što se traži ili da sam u konstrukciji koristio još nešto sem lenjira i šestara.
Citat: galet@world: Nisam napravio problem od tvog rešenja jer je ispravno.
Odavde ispada da sam sve uradio kako treba.
[ galet@world @ 21.02.2010. 16:45 ] @
Citat: Nedeljko: Odavde ispada da sam sve uradio kako treba.
Onda ispada da se i po mom predlogu sa h/4 može sve uraditi kako treba.
Ali pitanje ostaje - koji je to metod? [ Nedeljko @ 21.02.2010. 16:57 ] @
Pa, moglo je pod uslovom da h/4 konstruišeš a ne izračunavaš.
[ galet@world @ 21.02.2010. 22:35 ] @
Citat: Nedeljko: Pa, moglo je pod uslovom da h/4 konstruišeš a ne izračunavaš.
Ja zaista ne razumem na čemu ti insistiraš, možda pod izračunavanjem podrazumevaš
izračunavanje konkretne brojčane vrednosti dužine a ne i formalno odnosno principijelno
izračunavanje nekih odnosa ili veličina koje onda konstruišemo. Vrlo jednostavno je
konstruisati i h/4 i 3h/2, ali otkud meni h/4 i otkud tebi 3h/2? To nismo isisali iz prsta
nego smo morali sračunati u tom opštem obliku (a ne brojčano) i sami sebi dokazati da
tako može pa tek onda konstruisati - zar ne? [ Nedeljko @ 22.02.2010. 07:06 ] @
Pa, prvo ti nisi bio jasan na šta misliš pod izračunavanjem u konstrukciji. Čovek bi pomislio da meriš duži, pa onda izračunavaš dužine onoga što ti treba. No, taj račun o kome sad pričaš svakako nije sastavni deo konstrukcije, već analize. U konstrukciji se koriste samo lenjir i šestar. Tu se govori o spravama, a račun svakako nije sprava.
[ galet@world @ 22.02.2010. 08:07 ] @
U algebarskom metodu rešavanja geometrijskih zadataka svejedno je kako se
izračunava neka veličina - brojčano ili u opštem obliku - bitno je da ta veličina nije
rezultat konstruisanja već računa (analize). Dakle, analitički si dobio 3h/2 ili h/4
a ne konstruisanjem, naravno, te veličine posle možeš konstruisati, ali tek pošto si
ih analitički odredio tj. tek pošto si ustanovio šta ćeš konstruisati u cilju rešavanja
zadatka
[ Nedeljko @ 22.02.2010. 11:05 ] @
Konstrukciji uvek prethodi analiza, kako god rešavao zadatak.
[ zzzz @ 22.02.2010. 14:05 ] @
Ako pojmove "podudarnost" ili "poklapanje" priznamo
za geometrijske relacije,onda nam ne treba ništa
drugo od analitike za rješavanje ovog zadatka.
[ Nedeljko @ 22.02.2010. 17:41 ] @
Ali su analiza, konstrukcija, dokaz i diskusija svakako potrebni.
[ zzzz @ 22.02.2010. 18:19 ] @
To da,ali nije bilo neophodno algebarsko izračunavanje.
A izračunato je da je omjer strane i visine tetraedra
jednak korijenu iz 1.5.
Inače mislim da su su hibridni dokazi korisni i opravdani.
[ Nedeljko @ 22.02.2010. 19:07 ] @
Znači, Pitagorina teorema nije geometrijska. Vaauuu.
[ galet@world @ 22.02.2010. 20:23 ] @
Citat: Nedeljko: Konstrukciji uvek prethodi analiza, kako god rešavao zadatak.
Da, ali analiza ne mora biti sračunavanje, pa konstruisanje sračunatog, pa potom konstruisanje
traženih geometrijskih veličina - jer ako se tako radi onda se takav metod konstruisanja zove
algebarski. [ Nacrtna geometrija @ 21.11.2011. 21:00 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|