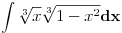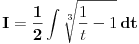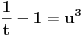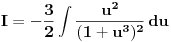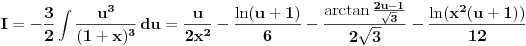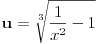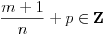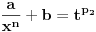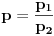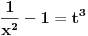[ Kolins Balaban @ 14.02.2010. 12:08 ] @
izracunati sumu reda

po dalamberu red konvergira, sto znaci da se moze naci suma... ali je ne mogu naci :(



ovo ne mogu ni pomaketi :( probao sa nekakvim smjenama, ali samo se zakomplikuje izraz. Ako moze bilo kakva pomoc. Hvala :)

[ Nedeljko @ 14.02.2010. 13:54 ] @
To što je red konvergentan znači da njegova sum apostoji, a ne da se može izraziti preko celobrojnih konstanti i elementarnih funkcija.

U ovom konkretnom slučaju se red može sumirati.

, gde je .

Dakle, , pa je .
[ petarm @ 14.02.2010. 14:48 ] @
Lepo Nedeljko! :)

Možda je ovako postupnije







Gde je





[ petarm @ 14.02.2010. 17:33 ] @
Citat:
Kolins Balaban: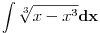 


ovo ne mogu ni pomaketi :( probao sa nekakvim smjenama, ali samo se zakomplikuje izraz. Ako moze bilo kakva pomoc. Hvala :)


Ovo deluje da moze da se resava kao integral binomnog diferencijala!

Predstavis ga u formi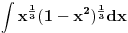



Pogledaj ovu temu http://www.elitesecurity.org/t90116-0

[Ovu poruku je menjao petarm dana 14.02.2010. u 18:48 GMT+1]

[Ovu poruku je menjao petarm dana 14.02.2010. u 23:22 GMT+1]
[ Nedeljko @ 14.02.2010. 21:42 ] @
Pardon, on ima integral .

Može se rešavati smenom



Sada ide smena



Sada imaš integral racionalne funkcije.
[ Nedeljko @ 15.02.2010. 17:37 ] @
Pardon, treba



za .
[ Cabo @ 15.02.2010. 18:13 ] @
Citat:
petarm: Ovo deluje da moze da se resava kao integral binomnog diferencijala!

Predstavis ga u formi




Što „deluje“, jeste! Pravo zboriš.

I to je tip „“, koji se rešava smenom , gde je .

Prevedeno na srpski, smena je .
[ Kolins Balaban @ 16.02.2010. 12:21 ] @
hvala na pomoci :) integral sam uradio kao binomni diferencijal...