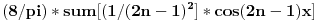[ majoneza @ 17.02.2010. 19:33 ] @
|
[ miki069 @ 17.02.2010. 22:03 ] @
i smenom pi-2*x = t se isto dobije da je a0 = 0.
Moraš prvo dodefinisati funkciju jer pi-2*x nije parna funkcija a traži ti se razvoj po kosinusima. Detalje pogledaj na: http://www.matematiranje.com/V...atematika/furijeovi_redovi.pdf Ne menja rezultat, ali bez toga nije formalno ispravno. Krajnji rezultat je ispravan. [ majoneza @ 18.02.2010. 00:11 ] @
Je, u pravu si. Sa smjenom ispada isto (šta je i logično) jer sam ja falia glupost vratit nazad smjenu.
To znam da je treba proširit po parnosti, pa je onda manje više ista stvar. Da li postavljena jednadžba izgleda ovako? 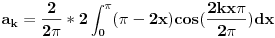 pa je to onda:  pa parcijalna integracija  nakon parcijalne: 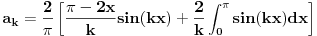 i šta sad. Kako dalje? Mislim, znam kako, ali ovo šta ja dobijam nema nikakvog smisla. [ miki069 @ 18.02.2010. 01:14 ] @
Posle ovog koraka prvi član u zagradi ti je isto u granicama X ide od 0 di pi.
Daje rezultat 0 jer je sin(n*pi)=0. Ili uradi prvo ceo integral kao neodređen pa onda zameni granice X od nula do pi. Drugi član ti je tabličan integral koji posle zamena granica i raspisivanja članova daje formu iz rezultata. Vodi računa da je cos(n*pi)=1 za parne n, a -1 za neparne n. Ovo tvoje k je isto što i n iz reda. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|