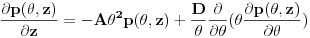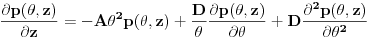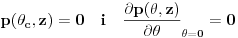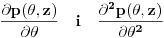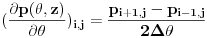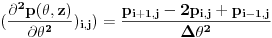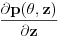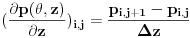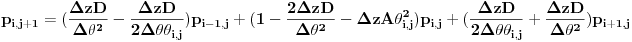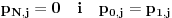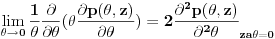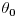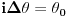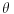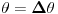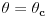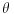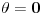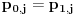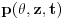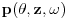[ bdrljaca @ 22.02.2010. 09:45 ] @
Naime, imam problem sa programiranjem u Fortranu koji je sledeće prirode. Treba numerički rešiti parcijalnu diferencijalnu jednačinu metodom kočnanih razlika. Jednačina je prikačena.


Kod koji sam napisao je:
Code:
PROGRAM NUMERICKO

  dimension pr(-1:100,0:300000)                                                        
  
  REAL theta,DZ,D,A,c,indeks,Z,korakuglovni, ugao, kriticni
  INTEGER i,j,n,m
  DOUBLE PRECISION  w,Dtheta
  PARAMETER (c=299792458, w=314, korakuglovni=0.5, DZ=0.001, kriticni=20,D=0.000117, A=0,4, indeks=1.5 )

  PRINT *,'Unesite duzinu vlakna'     
  READ (*,*)Z

  PRINT *,'Unesite ugao pod kojim se ubacuje signal u stepenima u stepenima' !ugao mora da bu edmanji od 15 stepeni     
  READ (*,*)ugao

  Dtheta=korakuglovni*0.017453292
  theta=ugao*0.017453292
  thetaC=kriticni*0.017453292

  m=Z/DZ
  n=kriticni/korakuglovni
  PRINT *,n,m    

  open(5,FILE='popuna1.dat')
  
  !unos impulsa na pocetku vlakna

  DO i = 0, n, 1        
    DO j = 0, m, 1        

         if (((i*korakuglovni).EQ.ugao .AND. (j.EQ.0))) then

            pr(i,j) = 1
            
        else 

            pr(i,j) = 0

        end if
      END DO
   END DO

  open(6,FILE='racun1.dat')

  DO j = 0, m-1, 1
    DO i = -1, n+1, 1 
      
     if ((i .LT. 0) .OR. (i.GT.n-1)) then

            pr(i,j)=0
    else
     
     if (i .EQ. 0) then 

         p1=(2.*DZ)/(Dtheta**2.)
         p2=(4.*DZ)/(Dtheta**2.)-1.
         p3=(2.*DZ)/(Dtheta**2.)
            pr(i,j+1)=p1*pr(i-1,j)-p2*pr(i,j)+p3*pr(i+1,j)

     else

     if (i .EQ. 1) then          

          pr(i,j)=pr(0,j)
                
         else
              
                p4=(DZ*D)/(Dtheta**2.)-(DZ*D)/(2.*Dtheta*i*Dtheta)
                p5=1.-(2.*DZ*D)/(Dtheta**2.)-DZ*A*((Dtheta*i)**2.)
                p6=(DZ*D)/(2.*Dtheta*i*Dtheta)+(DZ*D)/(Dtheta**2.)
                pr(i,j+1)=p4*pr(i-1,j)+p5*pr(i,j)+p6*pr(i+1,j)
  
            end if
        end if
      end if
      END DO
  END DO

  open(7,FILE='ispis1.dat')
  
   DO j = m-2, m, 1
      DO i = 0, n, 1
     if (j .EQ. m) then     
         write (7,*)i,pr(i,j)
     end if
     END DO
  END DO

END PROGRAM 


problem je u tome što funkcija treba da daje raspodelu koja se pri većim dužinama pomera ka 0 (na X osi), tj. maksimum treba da je na 0, a meni funkcija ima približni oblik Gausove raspodele oko vrednosti ugla pod kojim je ubačen signal. Znam da je problem negde u programiranju, ali ne znam gde. Prva tri uslova u glavnoj petlji pretstavljaju granične uslove.

Ako neko može da pomogne bio bih veoma zahvalan.


Ako je potreban još neki podatak tu sam
[ Časlav Ilić @ 23.02.2010. 10:34 ] @
Trebalo bi da navedeš jednačinu i granične uslove, sa očekivanim opsegom ulaznih konstanti, i kakvu diskretizacionu šemu primenjuješ (trenutno si zakačio samo krajnju diskretizaciju).

Da ne bi skenirao rukopisne formule, vidi http://www.elitesecurity.org/t35291-Sve-La-TeX-na-ovom-forumu .
[ bdrljaca @ 24.02.2010. 09:52 ] @


Jednačina je: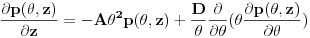

što kad se sredi daje: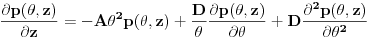

gde je: A-faktor multiplikacije drugog reda u izrazu za koeficijent gubitka snage
D-koeficijent sprezanja
z-dužina vlakna
θ-ugao prostiranja svetlosti u odnosu na osu vlakna

Granični uslovi su: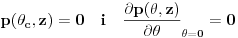

Primenom eksplicitnog metoda konačnih razlika, koristeći:

1) šemu centralne razlike za izvode 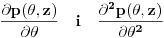dobijamo:





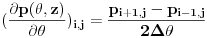
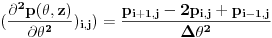
2) šemu prednje razlike za izvod 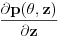dobijamo:



_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

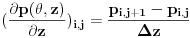
[Ovu poruku je menjao bdrljaca dana 24.02.2010. u 11:11 GMT+1]

[Ovu poruku je menjao bdrljaca dana 24.02.2010. u 11:15 GMT+1]

[Ovu poruku je menjao bdrljaca dana 24.02.2010. u 11:19 GMT+1]
[ bdrljaca @ 24.02.2010. 10:49 ] @
dalje jednačina 2 postaje:




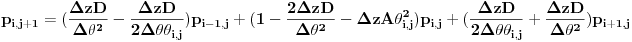
pri čemu granični uslovi postaju: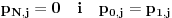

Da bismo izbegli problem singularnosti u tačkama θ=0 koristimo: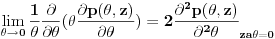


Upadni snop svetlosti je u obliku ravanskog talasa dat pomoću Dirakove delta funkcije: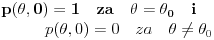

gde je 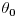upadni ugao svetlosti u odnosu na osu vlakna.

[ Časlav Ilić @ 24.02.2010. 12:17 ] @
Trenutno me kopkaju dve stvari.

Prvo, u uslovu:
Code:
if (((i*korakuglovni) .EQ. ugao ...

pošto se radi o realnim vrednostima, ne vidim kako može da se pogodi tačno 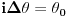. Ali, ako se ne pogađa, to bi značilo da program zapravo ne uspostavlja početni uslov, već da računa sa nekim „šumom“. Kako god bilo, ovaj uslov treba da bude:
Code:
abs(i * korakuglovni - ugao) .lt. Dtheta

(Takođe nema razloga da postavljaš -slojeve posle prvog na nulu, pošto je jednačina parabolička po .)

Drugo, nije mi jasna ova vratolomija sa levim graničnim uslovom. Koje je opravdanje za 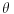-sloj -1 fiksiran na nulu (pa onda računanje sloja 0 preko limita)? Ja bih rekao da ovde odgovara prost Nojmanov uslov, i da se petlje svode na:
Code:
! Početni uslov.
do i = 0, n
    if (abs(i * korakuglovni - ugao) .lt. Dtheta) then
        pr(i, 0) = 1.0
    else
        pr(i, 0) = 0.0
    end if
end do

! Marširanje po z.
do j = 0, m - 1
    pr(0, j) = pr(1, j)  ! levi granični uslov, Nojmanov
    pr(n, j) = 0.0       ! desni granični uslov, Dirihleov
    do i = 1, n - 1
        p4 = ...
        p5 = ...
        p6 = ...
        p(i, j + 1) = ...
    end do
end do

(I levi i desni granični uslov za tekući -sloj treba postaviti pre unutrašnje petlje.)

Ako i sa ove dve izmene ne radi kako je očekivano, onda treba ispitati uslove stabilnosti šeme. Pošto je jednačina nelinearna, ali „skoro“ linearna, onda bi trebalo da može Fon Nojmanova analiza za reprezentativne linearizacije (npr. pri 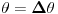i 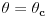) i date koeficijente i .
[ bdrljaca @ 24.02.2010. 12:46 ] @
Hvala puno, probaću pa ću se javiti.

sve sam probao sem da stavim uslove pre 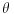petlje

ovo ostalo sam lupao jer znam da treba da driftuje ka 0, ali nikako nece, pa sam probao svakakve gluposti.

a, šta da radim sa ovim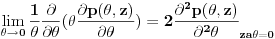

[Ovu poruku je menjao bdrljaca dana 24.02.2010. u 13:59 GMT+1]
[ Časlav Ilić @ 24.02.2010. 13:14 ] @
Pardon, treba abs(i * korakuglovni - ugao) .lt. korakuglovni, pošto je Dtheta u radijanima.

Citat:
bdrljaca: a, šta da radim sa ovim [...]


Pa ništa. Jeste singularitet u 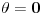, ali se automatski izbegava realizacijom Nojmanovog uslova .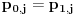

[ bdrljaca @ 24.02.2010. 18:19 ] @
Da, i meni je bilo jasno da se duplira uslov, ali pošto prvi put radim, rekoh da proverim. nisam stigao još da proverim ali ću se javiti ako bude problema.
Pozdrav
[ bdrljaca @ 25.02.2010. 09:26 ] @
Isprobao sam i radi. Hvala ti puno, a ako budem negde zakočio javiću se.
Treba da vidim kako da izračunam inverznu Furijeovu u slučaju kad mi je 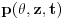, tj. iz 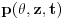prelazim u 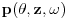pomoću Furijeove, pa prethodno pomenutu numeriku koristim za računanje u frekventnom domenu (modifikovanu naravno) i onda treba da se vratim u vremenski domen.
Meni jedino pada da fitujem funkciju koju sam dobio, pa da analitički tražim inverznu. Jel ti pada na pamet nešto elegantnije?
[ Časlav Ilić @ 26.02.2010. 10:20 ] @
Nisam ništa radio sa Furijeovim transformacijama, ali kao što postoji diskretna Furijeova transformacija, mora da postoji i inverzna diskretna Furijeova transformacija. Ona bi načelno bila bezbednija (u smislu da se ne unose spoljašnji elementi sumnjive prihvatljivosti) od analitičke aproksimacije pa transformacije, a možda i lakša za izvedbu (manje koda).
[ bdrljaca @ 26.02.2010. 11:09 ] @
Znam, nego nikad nisam radio :).
Još nešto da te pitam, da ne znaš kako bi izgledalo u Fortranu kada bih umesto Delta funkcije na ulazu ubacio Gausijan?