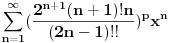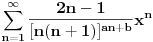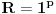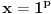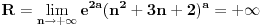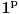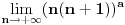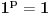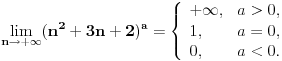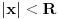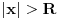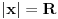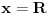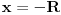[ different @ 23.02.2010. 06:58 ] @
|
[ different @ 23.02.2010. 08:38 ] @
1.
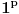 uvijek 1 ili -1. uvijek 1 ili -1.2. 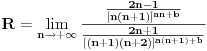 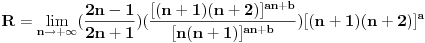 limes prvog faktora posljednjeh limesa je 1, drugog je 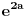 i treci je i treci je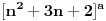 [Ovu poruku je menjao different dana 23.02.2010. u 09:53 GMT+1] [Ovu poruku je menjao different dana 23.02.2010. u 09:53 GMT+1] [Ovu poruku je menjao different dana 23.02.2010. u 11:12 GMT+1] [Ovu poruku je menjao different dana 23.02.2010. u 11:15 GMT+1] [ different @ 23.02.2010. 12:27 ] @
Nedjeljko, to mi je jasno, al na sta se dalje svodi ispitivanje konvergencije redova????
[ Cabo @ 23.02.2010. 13:30 ] @
Citat: different: 1. 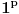 uvijek 1 ili -1. uvijek 1 ili -1.OMGWTF?! O.o Za koje je to 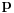 ispunjeno ispunjeno 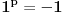 ? ?@ostatak pitanja: Ako jedan kriterijum ne radi (neodlučiv je), pokušaš drugim. [ different @ 23.02.2010. 14:55 ] @
@Cabo, ok sve to, al koje vrijednosti da uvrstim umjesto x???
[ Nedeljko @ 23.02.2010. 16:06 ] @
[ Nedeljko @ 23.02.2010. 18:44 ] @
Dakle, prvi red apsolutno konvergira za
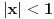 , a divergira za , a divergira za 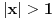 bez obzira na bez obzira na  . Za . Za  apsolutno konvergira po Gausu za apsolutno konvergira po Gausu za 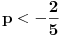 a divergira inače. Za a divergira inače. Za 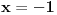 apsolutno konvergira po Gausu za apsolutno konvergira po Gausu za 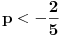 , divergira za , divergira za 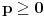 jer opšti član ne teži nuli, a za jer opšti član ne teži nuli, a za 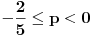 konvergira po Lajbnicu, ali po Gausu ne konvergira apsolutno, pa je ta konvergencija uslovna. konvergira po Lajbnicu, ali po Gausu ne konvergira apsolutno, pa je ta konvergencija uslovna.Drugi red za  konvergira apsolutno bez obzira na konvergira apsolutno bez obzira na  , za , za 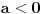 konvergira apsolutno za konvergira apsolutno za  i divergira za sve ostale vrednosti. Preostao je slučaj za i divergira za sve ostale vrednosti. Preostao je slučaj za 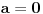 . Tada svakako konvergira apsolutno za . Tada svakako konvergira apsolutno za 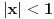 i divergira za i divergira za 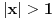 . Preostao je slučaj . Preostao je slučaj 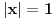 . Tada imamo apsolutnu konvergenciju akko je . Tada imamo apsolutnu konvergenciju akko je 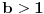 i divergenciju za i divergenciju za 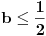 . Za . Za  red divergira za red divergira za 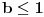 a za a za 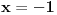 uslovno konvergira za uslovno konvergira za 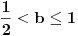 . .U realnom slučaju, stepeni red uniformno konvergira na kompaktima sadržanim u oblasti konvergencije. [ different @ 24.02.2010. 06:28 ] @
Nedjeljko, hvala puno...nisam dugo vremena rjesavao ove redove pa sam malo zaboravio ovu analizu konvergencije reda u zavisnosti od parametara, sad si me uveliko podsjetio na neke davno zaboravljene stvari....hvala jos jednom....
[Ovu poruku je menjao different dana 24.02.2010. u 08:10 GMT+1] Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|