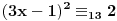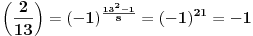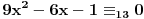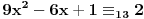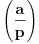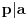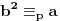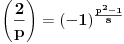Legendreov simbol

[ grancica @ 23.02.2010. 23:15 ] @

Imam problem. Naime ne znam kako se resavaju polinomijalne kongruencije pomocu Legendreovog simbola.

Zadatak glasi:

Koristeci osobine Legendreovog simbola ispitati resivost sledece kongruencije:

9x²-6x-1=0 (mod 13)

= je kongruentno

Napomonjem:
Legendreov teorem:

Neka je p prost broj,

P(x)=a_nxⁿ+a_n-1x^n-1+...+a₁x+a₀
polinom stepena n>1 (vece ili jednako 1) sa celobrojnim koeficijentima, pri cemu njegov vodeci koeficijent a_n
nije djeljiv sa p.
Tada polinom P(x) ima najvise n nekongruentnih korena moduo p.

Unapred zahvaljujem svima koji mi pomognu pri objesnjenju zadatka

_{[Ovu poruku je menjao grancica dana 24.02.2010. u 00:40 GMT+1]}

_{[Ovu poruku je menjao grancica dana 24.02.2010. u 00:40 GMT+1]}

[ Nedeljko @ 24.02.2010. 15:13 ] @

Ekvivalentno, da li je

.

Data kongruencija nema rešenja.

[ grancica @ 24.02.2010. 21:54 ] @

Pozdrav

Prvo da se zahvalim na pomoci i imam neka pitanja vezana za zadatak:
9x²-6x-1 nije isto sto i (3x-1)².

Kod ₁₃2 - 2 najveci stepen polinoma, a 13 je moduo.

Rezultat je -1, na osnovu njega konstatujemo da kongruencija nema resenja.

Ukoliko ima resenja koji rezultat treba biti

Hvala jos jednom

[ Nedeljko @ 24.02.2010. 22:58 ] @