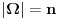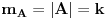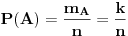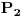[ ultraKeen @ 12.03.2010. 15:47 ] @
Zamislite igru koja se desava izmedju vise igraca, recimo njih 10 ili 20. Svaki igrac ima slobodu izbora odredjene kolicine meta bez limita: moze uzeti samo jednu metu ili recimo 100 meta. Raspored meta u igri je haotican, nije vezan za vlasnike tj. mete nisu grupisane u skupove istih vlasnika (mada je moguca i ta varijanta, sto mislim da nije bitno).

Mete bivaju upucavane jedna po jedna, nekim slucajnim/RND nacinom na koji volja igraca nema uticaja.

Pobednik igre je onaj igrac koji na kraju ostane sam u igri sa bar jednom metom, a svi ostali budu eliminisani jer su im upucane sve njihove mete.


Kada pre igre treba da uzmu - po svojoj volji - odredjenu kolicinu meta, igraci mogu da rezunuju na 2 nacina:

sto je VISE TUDjIH meta a MENjE MOJIH,
to je verovatnoca poGadjanja mojih meta MANjA
znaci treba da imam STO MANjE meta

sto je VISE MOJIH meta a MENjE TUDjIH,
to cu istrpeti VISE pogadjanja mojih meta a da ostanem u igri
tj. treba da imam STO VISE meta


Koji je rezon bolji?

Ili postoji neki treci rezon?
[ pajaja @ 12.03.2010. 16:07 ] @
Posto ti nije vazno koliko ces meta izgubiti, vec samo da ostanes sa bar jednom na kraju, druga strategija (sa sto vise tvojih meta) je ispravna.
[ ultraKeen @ 12.03.2010. 16:23 ] @
Slaze se...

A ako bi broj meta u pobednika bio bitan, za recimo velicinu neke nagrade?

Ako bi nagrada bila najveca kada pobednik ostane samo sa jednom metom?
[ Goran Rakić @ 12.03.2010. 17:17 ] @
Ako sam tačno postavio, verovatnoća da pobediš u igri sa najmanje jednom metom izborom k od n meta je pa je uz uslov maksimum upravo za , . hm, to def. nije dobro jer , jesam li pogrešio u sumiranju?

Trebalo bi uračunati i verovatnoću da ćeš moći da zauzmeš k meta u raspodeli, ali za to nema podataka u postavci.

Moj postupak je da je verovatnoća da su izvučene sve osim mojih x, jednaka , pa je tražena verovatnoća .

[Ovu poruku je menjao Goran Rakić dana 12.03.2010. u 18:55 GMT+1]

[Ovu poruku je menjao Goran Rakić dana 12.03.2010. u 18:55 GMT+1]
[ ultraKeen @ 12.03.2010. 17:35 ] @
Ako sam ja dobro razumeo formule, nema ogranicenja u broju uzimanja meta, tj. ono "n" nema limita - sta onda?

Svaki od igraca uzima koliko-god meta...

[Ovu poruku je menjao ultraKeen dana 12.03.2010. u 19:14 GMT+1]
[ Cabo @ 14.03.2010. 17:01 ] @
Citat:
Goran Rakić: 


Kad biraš od , onda skup elementarnih ishoda ima elemenata, a skup ima , pa je .

[ ultraKeen @ 14.03.2010. 21:31 ] @

Da prevedem "k/n": verovatnoca pobede sa samo jednom metom se linerno povecava sa brojem uzetih meta, tj. treba ih uzeti sto vise.

E sad' ... da li je to logicno?

Uzmimo ekstremni primer: svi igraci uzmu nekakav relativno veliki broj meta od 100 do 1.000, a samo jedan uzme 1.000.000.000 meta ... pa je verovatnoca tog zadnjeg da u igri ostane samo sa jednom metom mnogo veca od svih ostalih...

Da budem iskren, meni to ne lici da je logicno... pre bi se to moglo reci za verovatnocu da on (samo) pobedi, a ne da pobedi sa jednom metom...
[ zzzz @ 14.03.2010. 23:11 ] @
Pobednik igre je onaj igrac koji na kraju ostane sam u igri sa bar jednom metom, a svi ostali budu eliminisani jer su im upucane sve njihove mete.


Zar nije najbolje za sve te igrače da izaberu sve mete?
Nejasno mi je.
[ Goran Rakić @ 15.03.2010. 02:47 ] @
Citat:
Cabo: 

Kad biraš od , onda skup elementarnih ishoda ima elemenata, a skup ima , pa je .



Događaj A je bio da pobediš u igri, a ne da odabereš mete.

Greška je verujem u tome da uključuje i , tj. da pobeda sa 2 metom uključuje i pobede sa 1 metom pa P nije suma . Direktno po pravilu to onda ne znam da izračunam, tako da treba prići problemu sa neke druge strane.
[ ultraKeen @ 15.03.2010. 06:39 ] @
Citat:
zzzz: Pobednik igre je onaj igrac koji na kraju ostane sam u igri sa bar jednom metom, a svi ostali budu eliminisani jer su im upucane sve njihove mete.


Zar nije najbolje za sve te igrače da izaberu sve mete?
Nejasno mi je.


Broj meta nije ogranicen (beskonacan je), tako da je termin "sve" pomalo neupotrebljiv obzirom da se ne moze uzeti beskonacan broj; broj uzetih meta mora biti konacana ali je broj odakle se uzimaju mete beskonacan... Dakle svaki igrac moze uzeti koliko-god meta (a one su medjusobno sve iste).