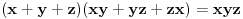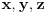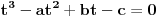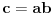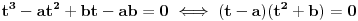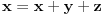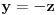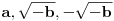Može i bez indukcije, preko Vijetovih formula.
Iz polazne jednakosti sledi
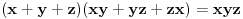
Ako su
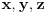
rešenja jednačine
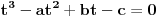
, onda po Vijetovim formulama sledi
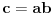
, pa dobijamo
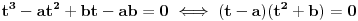
Prema tome, jedan koren jednačine upravo je koeficijent

, no po Vijetovim formulama, on je jednak zbiru sva tri korena. Zaključujemo da su dva od tri data broja uzajamno suprotni (tj. ako je npr.
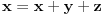
, onda je
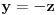
). Odatle traženi zaključak direktno sledi.
(Alternativna diskusija: brojevi
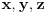
mogu se predstaviti kao
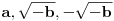
, gde opet imamo dva suprotna broja. Naravno, ako su dati brojevi realni, koeficijent

nužno će biti negativan.)