[ bdrljaca @ 26.03.2010. 11:17 ] @
|
| Zamolio bih nekog ako može da mi pomogne u sledećem problemu.
Naime, treba numerički rešiti vremenski zavisnu jednačinu protoka snage, koja ima sledeći oblik:
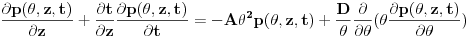
gde je: A-faktor multiplikacije drugog reda u izrazu za koeficijent gubitka snage
D-koeficijent sprezanja
z-dužina vlakna
θ-ugao prostiranja svetlosti u odnosu na osu vlakna
Granični uslovi su:
Nakon sređivanja imamo:
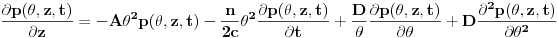
nakon primene Furijeove transformacije, i prelaska u frekventni domen jednačina postaje:
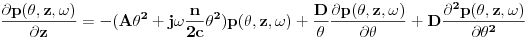
Kako je 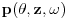 kompleksno, razdvajamo ga na realni i imaginarni deo, pa dobijamo: kompleksno, razdvajamo ga na realni i imaginarni deo, pa dobijamo:
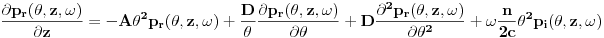
i
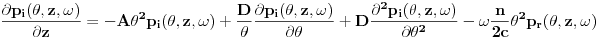
Primenom eksplicitnog metoda konačnih razlika, koristeći:
1) šemu centralne razlike za izvode 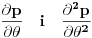 dobijamo: dobijamo:
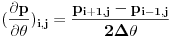
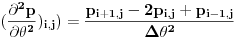
2) šemu prednje razlike za izvod 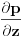 dobijamo: dobijamo:
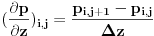
Na taj način dobijamo dve uparene jednačine:
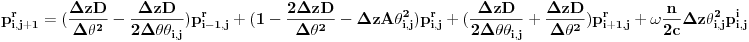
i
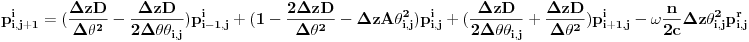
pri čemu granični uslovi postaju: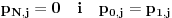
Da bismo izbegli problem singularnosti u tačkama θ=0 koristimo: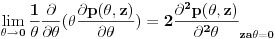
Ovo se dalje rešava numerički, pri čemu je upadni snop svetlosti, u vremenskom domenu, u obliku ravanskog talasa dat pomoću Dirakovog impulsa u vremenu, pod nekim uglom 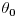 u odnosu na osu vlakna. u odnosu na osu vlakna.
Mene, kao prvo zanima kako će ulazni impuls izgledati u ferkventnom domenu, i kako ga implementirati na početku vlakna prilikom programiranja.
Drugo što me zanima je kako da dobijem frekventni odziv, nakon što sam dobio 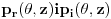 pri čemu za pri čemu za  uzimam određen broj frekvencija. uzimam određen broj frekvencija.
|
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.