[ milutinovicsm @ 28.03.2010. 23:23 ] @
Ako nekog ne mrzi,neka pokusa ovo da uradi:Ako su a,b,c,x,y,z realni pozitivni brojevi takvi da je a+x=b+y=c+z=1994,dokazati da je az+bx+cy<1994^2 (1994 na kvadrat).Ja sam pokusao preko sredina i nista ne dobijem,a video sam inace da je za 1.razred,samo nema resenja u zbirci.
[ Nedeljko @ 29.03.2010. 09:11 ] @
.
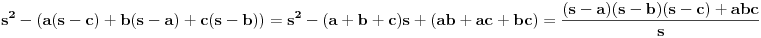
[ milutinovicsm @ 29.03.2010. 16:25 ] @
Jel bi mogao malo da mi pojasnis?
[ milutinovicsm @ 29.03.2010. 16:48 ] @
Jel ti je s=1994?
[ Nedeljko @ 30.03.2010. 01:13 ] @
a+x=b+y=c+z=s => x=s-a, y=s-b, z=s-c itd.
[ milutinovicsm @ 31.03.2010. 17:44 ] @
Hvala,sad mi jasno.
[ number22 @ 27.05.2010. 21:22 ] @
Imam i ja jednu nejednakost.
Ako je obim trougla manji od 2, dokazati da je
a^2+b^2+c^2+ab+bc+ca<=3
[ Nedeljko @ 27.05.2010. 22:11 ] @
Standardna smena za dužine ivica trougla

a=y+z
b=x+z
c=x+y

za neke x,y,z>0.

Jasno je da je a+b+c=2(x+y+z)<2. Treba dakle dokazati da je

(y+z)2+(x+z)2+(x+y)2+(x+z)(x+y)+(y+z)(x+y)+(y+z)(x+z)<3.

3(x2+y2+z2)+3(yz+xz+xy)<3

(x2+y2+z2)+(yz+xz+xy)<1

(x2+y2+z2)+2(yz+xz+xy)<1+(yz+xz+xy)

(x+y+z)2<1+(yz+xz+xy)

Ovo sledi iz

(x+y+z)2<1<1+(yz+xz+xy).
[ number22 @ 29.05.2010. 00:40 ] @
Zahvaljujem... A jednakost se i ne dostize pod ovim uslovom