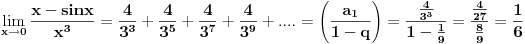Kad mozemo se zadrzati na prva dva clana!

Da, ali kako dati limes razviti u jedan čisto geometrijski brojni red.Suma tog reda je tačno 1/6.
Jako zanimljiv zadatak, ja sam ga uradio.Zbilja sada nemam vremena da postavim rješenje ali ću postaviti čim stignem.
Pokusajte jako je zanimljiv...

Dok čekamo to rešenje, u međuvremenu može i ovakvo:

Iz lako se dobija . Prema tome



Rešavanjem dobijene jednačine po nalazimo

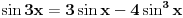
Koristeći jednakost imamo:



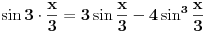
,odnosno vrijedi:



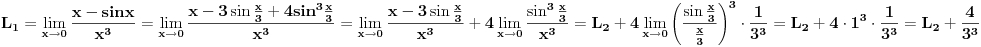
Sada, imamo:

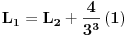
Dakle,




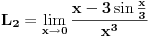
Uzimajući opet da vrijedi:

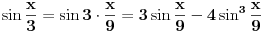
,imamo:



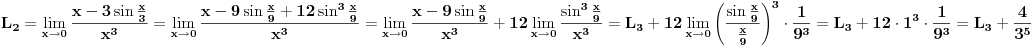
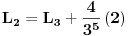
tj. , odnosno:



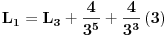
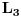
Rješavajući limes na analogan način, dobijamo:



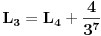
gdje je:

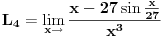
Dakle, imamo:



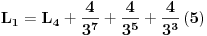
Vidimo da rješavanjem svakog narednog limesa dobijamo još jedan član geometrijskog niza



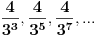
No, kako je ovaj proces beskonačan imamo da je naš zadani limes jednak sledećem geometrijskom redu:

Dali se slazete?

Puštajući u izrazu



da , dobija se da

.

Dakle, da bi rešenje bilo kompletno treba još dokazati da je .