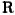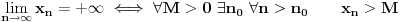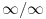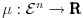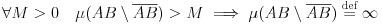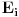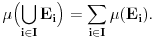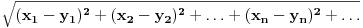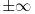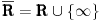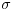[ toplim @ 15.04.2010. 19:10 ] @
|
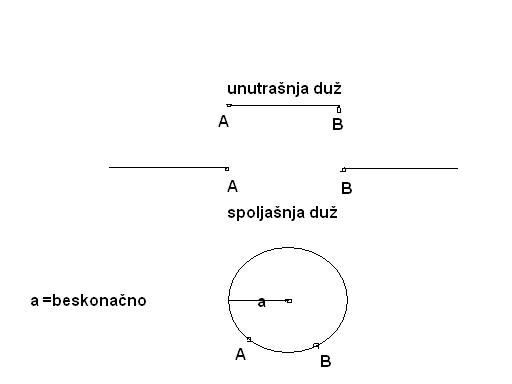
| Imamo dve tačke A i B. Najkraće rastojanje između ovih tačaka je duž AB. Da bi definisali najduže rasatojanje između ove dve tačke uvodimo pojam spoljašnje duži (sduž AB). Spoljašnja duž AB je duž koja je paralelna je sa duži AB i ne sadrži druge tačke duži AB, osim tačaka A i B.
Da li je ovo teorijski moguće?
Zbir duži AB i sduži AB je jednako beskonačno. Te dve duži zajedno čine krug beskonačnog obima.
Da li ima koristi od ovakve postavke? |
[ Cabo @ 15.04.2010. 21:46 ] @
Mnogo proizvoljnosti, sumnjiv cilj...
Hajde, krenimo prvo od svrhe: čemu sve ovo? Šta je ovde pitanje?
Drugo, u matematici je sve stvar definicija, konvencije. Jedino je logički aparat nepromenjiv.
Položi prvo Hiperboličku geometriju (još bolje: projektivnu), pa će ti mnoge stvari biti jasnije.
[ holononi @ 16.04.2010. 01:55 ] @
Ovo mi zvuči veoma poznato. Da li se ponovoi zagrevamo da izmerimo kružnicu 'iznutra' i 'spolja' ?
[ Cabo @ 16.04.2010. 15:56 ] @
Videćemo. :-/
[ toplim @ 17.04.2010. 18:03 ] @
Pitanje je koje je najduze rastojanje izmedju dve tacke A i B. Ne mozemo reci beskonacno. Jer to najduze rastojanje treba da zavisi od najkraceg. E sad zavisi kojim putanjama se ide. Ali jos jedna predpostavka:
Linija putanje ne sme da sadrzi tangente koje seku tu putanju. Znaci nema krivudavog kretanja onako u krug i bes smisla. Nadam se da imate predstavu.
[ Cabo @ 17.04.2010. 18:27 ] @
Citat: toplim: Pitanje je koje je najduze rastojanje izmedju dve tacke A i B. <-- Greška u startu; definiši rastojanje.
Ne mozemo reci beskonacno.
Jer to najduze rastojanje treba da zavisi od najkraceg. <-- Gde to piše?
E sad zavisi kojim putanjama se ide. <-- ??!
Ali jos jedna predpostavka: <-- preTpostavka Citat: toplim:
Linija putanje ne sme da sadrzi tangente koje seku tu putanju.
Znaci nema krivudavog kretanja onako u krug i bes [beZ] smisla. Nadam se da imate predstavu.
Zato ja rekoh da položiš Projektivnu (ili bar se informišeš o njoj). U Projektivnoj („Nacrtnoj“) geometriji, sve prave su „zatvorene“: svaka prava u ravni seče svaku pravu. Međutim, mera se ne definiše, pa ni 1-mera („rastojanje“).
Nadam se da sam malo razjasnio ono što sam rekao. [ holononi @ 17.04.2010. 20:13 ] @
Ako uzmemo da nema krivudanja i presecanja onda je takva duž izmedju tačaka A i B u stvari (veći) deo kruga beskonačnog prečnika. No to je u spurotnosti sa prvim tekstom gde se kaže
Citat: paralelna je sa duži AB i ne sadrži druge tačke duži AB, osim tačaka A i B
jer bi takav krug "pojeo" ne samo duž AB već i pravu kojoj pripada, ali duž ]A, B[ bi bila "najduže" rastojanje izmedju tačaka A i B. [ toplim @ 18.04.2010. 16:45 ] @
pa jeste takva duz veci deo kruga beskonacnog precnika(poluprecvnika), tj. kruznice. A paralelna je sa duzi AB. Znaci nacrtamo dve tacke A i B i ne povucemo duz izmedju njih nego suprotno od te dve tacke, znaci od tacke A u levo a od tacke B u desno i dobijemo dve poluprave. Ali te dve poluprave ser u beskonacnosti spajaju, tako da dobijamo spoljasnju duz AB.
 [ Cabo @ 18.04.2010. 17:14 ] @
Citat: holononi: Ako uzmemo da nema krivudanja i presecanja onda je takva duž izmedju tačaka A i B u stvari (veći) deo kruga beskonačnog prečnika.
U Euklidskoj ravni nema „kruga beskonačnog prečnika“, zato što u 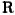 nema nesvojstvenog „broja nema nesvojstvenog „broja  “. “. Ovo je isti problem neshvatanja pojma beskonačnosti koji je imao (a pretpostavljam i još ima) Galet@world.
U Projektivnoj geometriji, on the other hand, nema mere, pa smo opet na istom: ovo pitanje nema smisla.
DODATAK: Odnos između geometrija je sličan „matrjoškama“. Afina geometrija ne razlikuje pojedinačne tačke (izbor osnove repera je proizvoljan). Projektivna ne razlikuje duži (nema meru).
[Ovu poruku je menjao Cabo dana 18.04.2010. u 18:37 GMT+1][ toplim @ 18.04.2010. 17:44 ] @
ako nacrtam pravu i kazemo da prava nije ogranicena tackama, zasto onda ne mozemo da nacrtamo dve poluprave na nacin kako sam pokazao i kazemo to je spojlasnja duz. Te dve poluprave su ogranicene sa jedne strane. Ali kao sto znamo da je prava neokgranicena tako isto mozemo da znamo da je duz ogranicena i da nije vazno gde se nalazi. cisto filozofski.
što se tiče R i pravila. Zar ne postoji neka oznaka za broj koji nije beskonacno ali je skoro beskonacno velik. trebalo bi da postoji.
[ Cabo @ 18.04.2010. 18:10 ] @
Prvo, garantujem da ne možeš da nacrtaš beskonačnu pravu.
Drugo, ako zanemarimo takve sitnice u izražavanju, u Euklidskom prostoru te dve poluprave nemaju dodirnih tačaka.
U Analizi se ne definiše „broj  “, već samo, recimo, oznake tipa 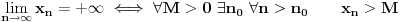 . Ali ne možeš da kažeš, recimo,  , 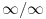 , itd. Takvi izrazi, u zavisnosti od njihove definicije, mogu imati vrednost, a mogu i nemati; zato se i zovu neodređeni izrazi.
Inače, ovde govorimo o osnovama čitavih predmeta sa Matematičkog fakulteta. Zato je veoma teško to objašnjavati nekome ko nije položio, recimo Analizu ili Osnove geometrije. [ holononi @ 18.04.2010. 18:43 ] @
Ovde niko ne insistira na geometriji osim tebe. Mnogi problemi se rešavaju bez primene geometrije tako da za sada neme razloga insistirati na projektivnoj i nacrtnoj geometriji. Diskusija je još uvek samo uopštena.
Nije mi jasno da li hoćeš da kažeš da diskusija o "najvećem rastojanju" nema smisla?
[ toplim @ 18.04.2010. 20:23 ] @
recimo imamo beograd i krusevac, najmanje rastojanje je duz koja ih spaja, tj, vazdusna linija. Najduze rastojanje je duz koja ih spaja ali okolao ako recimo krenes iz beograda tamo negde prema novom sadu i stignes u krusevac. Eto vidis da ima primene i najduze rastojanje. U ovom slucaju obe te duzi su delovi kruznog luka ili ti kruznice... malo prakse..
[ holononi @ 18.04.2010. 21:22 ] @
"Najduže rastojanje" ima veliku primenu, mnogo širu nego navedeni primer i zato pravilna postavka problema može da bude veoma interesantna. Posle ćemo trežiti metode za rešavanje.
[ Cabo @ 19.04.2010. 14:38 ] @
Citat: holononi: Ovde niko ne insistira na geometriji osim tebe. Mnogi problemi se rešavaju bez primene geometrije tako da za sada neme razloga insistirati na projektivnoj i nacrtnoj geometriji. Diskusija je još uvek samo uopštena.
Nije mi jasno da li hoćeš da kažeš da diskusija o "najvećem rastojanju" nema smisla?
Tako je. Zato što je „rastojanje“ mera, a mera u Euklidskom prostoru je funkcija 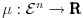 . Skup 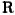 ne sadrži „broj  “. Moglo bi se dodefinisati, recimo, 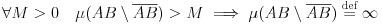 , ali takva funkcija nije mera, jer mera, po definiciji, treba da ispunjava svojstvo:
Citat:
* Countable additivity (or σ-additivity): For all countable collections 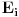 of pairwise disjoint sets in Σ:
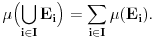
Citat: toplim: Najduze rastojanje je duz koja ih spaja ali okolao
To je slučaj koji je različit od opšteg. Prvo, koristi se kružnica umesto prave, a drugo, ta kružnica je konačnog prečnika.
Prava i krug su dve stvari, osim u Projektivnoj geometriji, gde nema mere.
Citat: toplim:U ovom slucaju obe te duzi su delovi kruznog luka ili ti kruznice... malo prakse..
Duž ne može da bude deo kružnog luka u Euklidskom prostoru. [ holononi @ 19.04.2010. 15:18 ] @
Da li hoćeš da kažeš da nema smisla diskutovati o konstrukciji pravilnog n-tougla jer to u opštm slučaju ne može da se reši pomoću šestara i lenjira ?
[ mokelet @ 19.04.2010. 15:23 ] @
Jedva čekam da se pridruži galet@world :-)
[ Cabo @ 19.04.2010. 15:54 ] @
Citat: holononi: Da li hoćeš da kažeš da nema smisla diskutovati o konstrukciji pravilnog n-tougla jer to u opštm slučaju ne može da se reši pomoću šestara i lenjira ?
Ne, već samo da nema smisla diskutovati o „beskonačnim dužima“ u Euklidskom prostoru. Zanimljivo je da mi upravo to radimo, pa je zaključak da se upravo bavimo besmislicama. :-/ [ holononi @ 19.04.2010. 16:58 ] @
Ovde problem nije postavljen u Euklidski prostor. Diskusija je uopštena. Po mom mišljenju ima smisla diskutovati o "najvećem rastojanju". Drugo je pitanje izbora metoda za rešavanje postavljenog problema. U nekim ranijim diskusijama smo imali slučaj da se uvode nove "definicije" već definisanih pojmova i tada je imalo opravdanja reagovati ali na ovoj temi bar za sada još nismo imali nešto tako.
[ Cabo @ 19.04.2010. 17:07 ] @
Citat: holononi: Ovde problem nije postavljen u Euklidski prostor.
O kom prostoru se onda radi? Projektivni ne može biti, zbog mere. [ mokelet @ 19.04.2010. 17:38 ] @
Kad smo već kod uopštenosti, da li je ispravno pretpostaviti da je u beskonačno dimenzionalnom prostoru rastojanje dve tačke beskonačno? [ holononi @ 19.04.2010. 19:05 ] @
Kakve implikativne veze ima vrednost valuacije rastojanja i kardinalnost prostora ?
[ mokelet @ 19.04.2010. 19:43 ] @
Pa ako je u n-dimenzionalnom postoru rastojanje (recimo Euklidsko) definisano sa 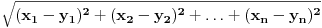 , odnosno ako je u beskonačno dimenzionalnom prostoru rastojanje 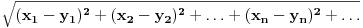 , da li je to beskonačno? Šta onda sa pojmom "najvećeg" rastojanja, ako je najkraće beskonačno? Da li je i ono beskonačno, i koji je odnos te dve beskonačnosti, ako su i jedno i drugo realni brojevi?
[Ovu poruku je menjao mokelet dana 19.04.2010. u 21:03 GMT+1][ holononi @ 19.04.2010. 21:54 ] @
Tebe u stvari zanima kako ja definišem beskonačno?
U računarskom programu nešto ovako 99 ili 99999 ili 1e300 a u matematici pod +∞ i -∞ podrazumevam tačke gomilanja skupa realnih brojeva (ako je tema ograničena na skup realnih brojeva).
Medjutim, kad si se već upustio u ovu diskusiju treba da znaš da postoje mere koje uzimaju vrednost +∞.
[ mokelet @ 19.04.2010. 22:32 ] @
Pod merom misliš na rastojanje ili meru skupa?
[ holononi @ 19.04.2010. 23:02 ] @
Mera je odgovor najpre onom ko je uveo meru u ovu temu, a ti si se nakačio.
[ AleksaP @ 19.04.2010. 23:30 ] @
Koliko sam ja ucio, ovo i nije teorijski moguce.
Ta duz sadrzi TACKE A i B. Tacke su tacke, ne moze biti sitnije od njih. Ne postoji deo tacke. Tako da duz od tacke A do tacke B, duz AB moze postojati samo kao najkraca, a ujedno i najduza. Tako da se ne moze racunati najkraci i najduzi put od tacke do tacke jer je to jedan isti put. Ili duzina...
A duz je skup tacaka od tacke A do tacke B, nije prava da ide beskonacno, ili poluprava od tacke da beskonacnosti... NE znam ni sto raspravljate o beskonacnosti, ovde je jedino velicina tacke beskonacna. Tacnije, ona je beskonacno mala. Koliko god gledali, ne mozemo da nadjemo njen pocetak i kraj, jer bi to bila duz a ne tacka.
Zato, ne moze biti duzi deo izmedju 2 tacke ili kraci deo...
Ja sam jos osnovac, tako da verovatno pricate o necemu daleko iznad osnovne skole, ali meni po svom sopstvenom znanju nema smisla...
[ mokelet @ 19.04.2010. 23:34 ] @
Citat: holononi:Mera je odgovor najpre onom ko je uveo meru u ovu temu, a ti si se nakačio.
Ništa te ne razumem. Kome onda odgovaraš? Ako kroz odgovor meni odgovaraš Cabou, onda si se ti nakačio. Ja sam samo naveo primer,
a nisi se ni potrudio da ga potvrdiš/osporiš.
Ako si rekao da je u pitanju opšta priča i ako si Cabou zamerio što se ograničio na projektivni prostor (jeste on prvi spomenuo meru, ali je
napomenuo da u projektivnom prostoru nema mere, a Euklidska mera ne poznaje 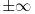 ), onda ni ti ne možeš tek tako da
definišeš 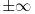 kao deo proširenog skupa realnih brojeva (u stvari možeš, ali kaži o kojoj meri se onda radi).
A tek ne možeš da uvodiš u priču "tačku nagomilavanja", jer to nije opšta priča.
I dalje čekam odgovor na pitanje koliko je rastojanje u beskonačno dimenzionalnom prostoru.
[Ovu poruku je menjao mokelet dana 20.04.2010. u 01:26 GMT+1][ AleksaP @ 19.04.2010. 23:45 ] @
Cek, cek... Zbir duzi AB i paralelne duzi koja sadrzi A i B je beskonacno?
Ne, to je 2* AB duz iliti 2AB... A to nije beskonacno jer je duz konacna.
Zar ne?
[ holononi @ 20.04.2010. 10:22 ] @
Ko nije shvatio moju primedbu u vezi valuacije rastojanja i kardinalnost prostora ne vredi da diskutujemo.
[ Cabo @ 20.04.2010. 11:14 ] @
Citat: holononi:postoje mere koje uzimaju vrednost +∞.
Šta je „vrednost  “? To nije element skupa 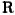 .
Ako uzmemo 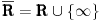 , da li je to polje? Važi li u njemu 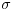 -aditivnost? [ mokelet @ 20.04.2010. 12:41 ] @
Citat: holononi: Ko nije shvatio moju primedbu u vezi valuacije rastojanja i kardinalnost prostora ne vredi da diskutujemo.
Malo manje nadutosti, molim.
Na koji prostor mislimo? Euklidov? Na koju meru mislimo? Euklidsku? OK. I šta sada sa kardinalnošću? I na koju kardinalnost misliš, kardinalnost skupa R u kojem izražavamo meru rastojanja ili na kardinalnost skupa N u kome izražavamo dimenziju? [ holononi @ 20.04.2010. 13:41 ] @
@Cabo
Na primer, kod spoljne mere važi σ-subaditivmost.
[ holononi @ 20.04.2010. 13:55 ] @
Eh da, prostor si ti uveo a ne pokretač teme. Time si ga sprečio da do kraja iskaže šta je hteo. A sada je diskusija uzela tok u pravcu koji možda nije bila namera inicijatora teme.
[ Cabo @ 20.04.2010. 15:17 ] @
Citat: holononi: Eh da, prostor si ti uveo a ne pokretač teme. Time si ga sprečio da do kraja iskaže šta je hteo. A sada je diskusija uzela tok u pravcu koji možda nije bila namera inicijatora teme.
Kako sam ga sprečio?
Inicijator teme je laik i/ili ne zna Afinu geometriju, Projektivnu geometriju, Analizu 1, 2, Algebru ...
[ holononi @ 20.04.2010. 18:04 ] @
To što je neko laik nije osnov za diskvalifikaciju.
Zašto si omastio ono sub ? Neki problemi ?
[ toplim @ 20.04.2010. 19:01 ] @
Ideja je da se dokaze da je + beskonacno i - beskonacno jednako. Tj. da u prostoru n-dimenzije - i + beskonacno su iste tacke.
Tada dolazimo do zakljucka da postoji i sduz IABI koja prolazi kroz tacku beskonacno. Ali neko uvek potencira da beskonacno ne moze biti tacka i da to nije dimenzija. Tacno, matematicki gledano. Ali ako beskonacno nije tacka kako mozemo dokazati da se to beskonacno nalazi u prostoru n- dimenzija. Tada dolazimo do zakljucka da beskonacno ne postoji.
[ Cabo @ 21.04.2010. 15:51 ] @
Citat: toplim: Tacno, matematicki gledano.
Nematematičke teme nisu predmet foruma „Matematika“.
Citat: toplim: Ali ako beskonacno nije tacka kako mozemo dokazati da se to beskonacno nalazi u prostoru n- dimenzija. Tada dolazimo do zakljucka da beskonacno ne postoji.
Tačno; ali zavisi gde. U „stvarnom svetu“, skupu realnih brojeva i Euklidskim prostorima, beskonačno ne postoji.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|