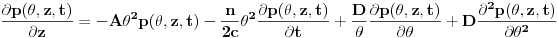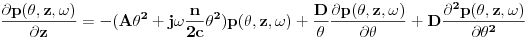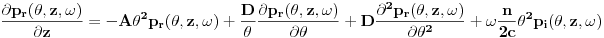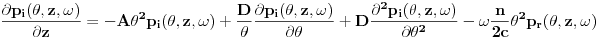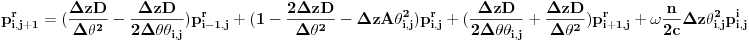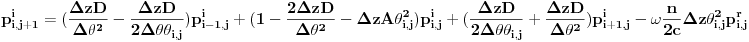|
|
[ bdrljaca @ 20.04.2010. 22:16 ] @
|
| Da li zna neko da mi kaže kako da isprogramiram signal koji je kombinacija vremenskog delta impulsa i prostorneg Gausove raspodele, ali u frekventnom domenu, tj. kako bi to izgledalo nakon Fourier-ove transformacije?
Za više detalja ili mi pišite ili pogledajte prethodne teme koje sam postavio.
Hvala unapred.
|
[ robert63 @ 21.04.2010. 00:00 ] @
Citat: bdrljaca:,,,Kako da isprogramiram signal,,,
--ovo je vec dovoljno,
A tek onda;
Citat: bdrljaca:,,kombinacija vremenskog delta impulsa i prostorneg Gausove raspodele,
A kako To izgleda nakon:
Citat: bdrljaca:,,,Kako bi to izgledalo nakon Fourier-ove transformacije ? [ yugaja @ 21.04.2010. 09:09 ] @
Matlab?
[ bdrljaca @ 21.04.2010. 13:38 ] @
@robert63
ne razumem te, ali ni najmanje.
Ako možeš i hoćeš da pomogneš, onda to uradi.
Ako ne razumeš onda pitaj.
Ako sam nešto lupio, možda i ne poznajem materiju najbolje, pa zato i tražim pomoć.
[ milanche @ 21.04.2010. 15:35 ] @
Citat: Da li zna neko da mi kaže kako da isprogramiram signal koji je kombinacija vremenskog delta impulsa i prostorneg Gausove raspodele, ali u frekventnom domenu, tj. kako bi to izgledalo nakon Fourier-ove transformacije?
Za više detalja ili mi pišite ili pogledajte prethodne teme koje sam postavio.
Hvala unapred.
Ako sam te dobro shvatio treba ti signal koji kombinuje:
1) dirakov impuls u vremenu, i
2) vremenski signal ciji je spektar kriva Gausove raspodele u frekventnom domenu.
Dirakov impuls u vremenu siguran sam da znas kako da napravis.
Drugi deo:
a) generises signal belog suma (obican random generator je dovoljan), koji ima ravnu spektralnu
karakteristiku.
b) podelis signal belog suma na sekcije od 2^N semplova. Na svakoj sekciji semplova uradis sledece korake:
------------------------------------------------------------------------------------------------------
c) prevedes taj signal Furijeovom transformacijom u frekventni domen, tj. izracunas mu spektar (magnitude i faze,
dobijene kao moduo i argument kompleksnih brojeva).
d) moduo spektra (koji je vrlo priblizno konstanta za sve frekvencije, ali mora da malo varira tu i tamo da bi sve
bilo realnije) pomnozis sa krivom Gausove raspodele, za koju treba da znas centralnu frekvenciju (tj. oko koje je
kriva centrirana) kao i sigma parameter (koji odredjuje sirinu zvona krive).
e) tako dobijen rezultantni spektar vratis nazad u vremenski domen, dobivsi sekcije od 2^N vremenskih semplova
f) novodobijenu sekciju semplova po windowed overlap-add metodu izkombinujes sa predhodnom kolekcijom, i rezultat
slazes na vremensku osu.
-----------------------------------------------------------------------------------------------------
To je ukratko.
Predpostavljam da vec odprilike znas detalje kako se radi windowing (Keiser-Bessel modifikovana funkcija je vrlo
popularna za te svrhe) i FFT (direktna i inverzna transformacija). [ robert63 @ 21.04.2010. 16:08 ] @
@bdrljaca
-NARAVNO da hocu da pomognem !
Ali za vreme svog bavljenja Elektronikom,
jos NISAM cuo ovu Tvoju " Kombinaciju Reci"--postavljenih tim redom,
NE Pod**bavam,nego mi je jako zao sto ne razumem o cemu pricate.
Veruj mi,
100-Andraka sam prosao,cuo,gledao,popravljao,remontovao ali ja stvarno:
-NEMAM POJMA o cemu VI razgovarate ???
@bdrljaca
-I Z V I N I jos jednom,komentar nije zlonameran,
ali JA ocigledno NISAM dorastao temi.
-samo nastavite,prijatno vam bilo,
( nemoj da moje izletanje nesto remeti u resenju zadatka)
Pozdrav Ekipi !
[ bdrljaca @ 21.04.2010. 16:42 ] @
@milanche
Ne baš. Treba da dobijem prostorno-vremenski impuls, kojem samo prostorna raspodela ima oblik Gausove krive, dok je vremenska zavisnot opisana samo delta impulsom. Tako dobijenu raspodelu treba da prevedem u frekventni domen i da pustim kroz određenu jednačinu prevedenu u konačne razlike i na kraju dobijem izlaznu raspodelu koja zavisi od frekvencije i jednog prostornog parametra (u mom slučaju ugla), pa da tada radim inverziju u vrem. domen. Mene buni to što kada se delta impuls prevede u frekventni domen on postaje 1, tj. nije funkcija od 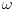 , a ja treba da nacrtam grafik zavisnosti amplitude signala od 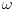
Drugi problem je u tome što sam ja fizičar, pa se nisam dosad sretao sa ovakvim stvarima ranije, a i literaturu ne mogu da nabavim.
[ milanche @ 21.04.2010. 17:25 ] @
@robert63:
ne se sekiras - to je DSP (digitalna obrada signala).
Ne bih se zakunuo da spada u elektroniku, ali je to najbliza rubrika od svih postojecih.
[ milanche @ 21.04.2010. 17:40 ] @
Citat: @milanche
Ne baš. Treba da dobijem prostorno-vremenski impuls, kojem samo prostorna raspodela ima oblik Gausove krive, dok je vremenska zavisnot opisana samo delta impulsom. Tako dobijenu raspodelu treba da prevedem u frekventni domen i da pustim kroz određenu jednačinu prevedenu u konačne razlike i na kraju dobijem izlaznu raspodelu koja zavisi od frekvencije i jednog prostornog parametra (u mom slučaju ugla), pa da tada radim inverziju u vrem. domen. Mene buni to što kada se delta impuls prevede u frekventni domen on postaje 1, tj. nije funkcija od 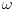 , a ja treba da nacrtam grafik zavisnosti amplitude signala od 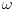
Drugi problem je u tome što sam ja fizičar, pa se nisam dosad sretao sa ovakvim stvarima ranije, a i literaturu ne mogu da nabavim.
Hm, tough luck.
Ja sam audio/video DSP inzenjer, mahom se bavim signalima u 1D (audio) ili 2D(slika, dosta davno), a
u ovom tvom slucaju se izgleda radi o 3D signalu. Nije mi bas daleko da shvatim kako bi trebalo da se
uradi, samo da budem iskren - nikada tako nesto nisam radio u domenu trodimenzionalnih signala.
Ako sam dobro razumeo, posmatrano u frekventnom domenu, signal treba da se ponasa kao kad neko
munjevito rasiri i skupi kisobran (ako oblik Gausove krive shvatimo kao neku vrstu 'kisobrana', mada ne
lici bas uvek i sasvim, ali 'ajde).
Sta da pocnes da gledas (nadji primere za audio, tj. jednodimenzionalne signale, pa kad to ukapiras idi na 3D)
1) Fourier-ova transformacija (teorija) kao i efikasni nacini numericke implementacije (FFT)
2) sectioned signal processing (overlap-add, overlap-save metodologija, cesto se srece primena ovih pristupa na
konvoluciju signala, ali moze i na druge funkcije signala, tj. u domenu filtriranja pomocu FFT)
3) windowing (kome je trebalo i zasto, kako se primenjuje, izbor window krive). Poseban osvrt na Kaiser-Bessel
window function.
[ bdrljaca @ 22.04.2010. 09:13 ] @
u principu problem jeste 3d, ali se zbog kružne simetrije radi kao 2d. Jel možeš da mi pojasniš kako se dobija zavisnost sa slike, tj. koji opseg uzimam za 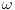 .
još jedna stvar, zanemarimo gausovu raspodelu i pretpostavimo da hoću da ubacim samo delta funkciju, kako bi to izgledalo i koji opseg za 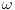 bi onda bio. Ako možeš pogledaj molim te jednačine koje sam postavio na temi DOBIJANJE FREKVENTNOG ODZIVA možda će ti biti nešto jasnije.
hvala ti u svakom slučaju [ milanche @ 23.04.2010. 06:23 ] @
Citat: Jel možeš da mi pojasniš kako se dobija zavisnost sa slike, tj. koji opseg uzimam za 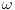 .
Slike u poslednjoj koloni su nista drugo nego slike u srednjoj koloni nacrtane u koordinatnom sistemu u kojem je na abscisi
frekvencija u log razmeri, a na ordinati moduo spektra, takodje u log razmeri.
Dakle, jedina misterija koju treba da ti objasnim je kakva je veza izmedju slika krajnje levo i slika u sredini. Objasnjenje te
zagonetke je krajnje prosto - cim pocnes da ceprkas oko Fourier-ove transformacije, ubrzo dodje na red izracunavanje
transformacije za neke tipicne proste slucajeve signala, i ovo je upravo to.
http://fourier.eng.hmc.edu/e101/lectures/handout3/node3.html
Fourier-ova transformacija pravougaonog impulsa (levi gornji ugao) je funkcija sin( 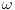 )/ 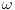
poznatija kao sinc( 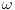 ), nacrtana na slici u najgornjem redu u sredini. Slicna stvar je u donjem redu - Fourier-ova
transformacija trougaone funkcije je sinc^2( 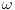 ).
[ bdrljaca @ 23.04.2010. 08:17 ] @
Pa nije baš samo to 
Tako sam i mislio, ali nisam bio 100% siguran.
Veći problem mi je kako da takava signal ubacim na ulazu u numerički proračun. Da li treba svaku frekvenciju iz određenog opsega
da ubacim samo kao broj(koji za tu frekvenciju dobijam kao sinc(  )) pa gledam šta se dešava sa tom frekvencijom, i to ponovim za sve frekvencije?
Drugi problem je što ne znam da li moram to da radim za sve frekvencije iz opsega ili mogu samo za određene pa da aproksimiram krivu na osnovu tih tačaka.
Ima tu još problema, ali me ovi najviše muče za početak. [ milanche @ 23.04.2010. 17:37 ] @
Citat: Veći problem mi je kako da takava signal ubacim na ulazu u numerički proračun. Da li treba svaku frekvenciju iz određenog opsega
da ubacim samo kao broj(koji za tu frekvenciju dobijam kao sinc()) pa gledam šta se dešava sa tom frekvencijom, i to ponovim za sve frekvencije
Izuzetno je bitno da sebi razjasnis sta je sta.
U ovom slucaju pocinjes od spektra, jer je to zahtev zadatka (tj. traze ti Gausovu krivu u frekventnom domenu).
Krajnji cilj su ti semplovi signala u vremenu.
Konverziju izmedju spektra i vremenskog signala obavlja inverzna Furijeova transformacija.
Ulazni podaci u inverznu Furijeovu transformaciju su semplovima spektra. To su kompleksni brojevi, ciji moduo je
u opsegu [0,1] i predstavlja amplitudu sinusoidalne frekventne komponente, a argument je u opsegu [0,2pi] predstavlja
pocetnu fazu sinusoidalne frekventne komponente.
Kljucno pitanje: u kojim tackama na frekventnoj osi racunati semplove spektra ?
Da bih ti dao odgovor na ovo pitanje, moramo malo da se odmaknemo unazad:
Neki osnovni postulat algoritma brze Furijeove transformacije je da ako uzmes N semplova vremenskog signala, i na
osnovu njih izracunas procenu spektra, dobices rezultat koji predstavlja semplove spektra signala u tackama k*Fs/N
na frekventnoj osi.
Dakle: imas vremenski signal semplovan frekvencijom Fs, uzmes od signala N vremenskih semplova, njima nahranis FFT algoritam
koji ce da ti ispljune N kompleksnih brojeva koji nisu nista drugo nego semplovi spektra u tackama k*Fs/N, gde k = [0,N-1].
Sto je veca frekvencija semplovanja i veca kolekcija od N semplova, FFT ti daje finiju rezoluciju procene spektra.
U tvom slucaju, prica krece s obratne strane - pocinjes od spektra ciju envelopu znas (neka Gausova kriva), i treba od nje
da sintetizujes vremenski signal, semplovan ucestanoscu Fs. Ako semplove spektra izracunas na frekvencijama k*Fs/N, i to
ubacis kao ulaz na inverznu FFT, rezultat ce ti biti N semplova vremenskog signala.
[ milanche @ 23.04.2010. 17:41 ] @
Sada, medjutim, sledi lukaviji deo price:
Ako si se poradovao da ces samo tako moci da kreiras redom (u petlji) kilometre vremenskog signala, rano si se poradovao.
Mrzi me da pisem (zurim na posao), ali ti savetujem da procitas o tehnici windowing-a + overlap-add-a, jer to je upravo kako
treba da se obavi 'slaganje' kreiranih kolekcija od N vremenskih semplova da bi se dobilo ono sto treba.
[ Odin D. @ 24.04.2010. 07:18 ] @
Ako me sjecanje dobro sluzi (da ne listam sad knjige)... cini mi se da Furijeovom transformacijom Gausove krive dobijes opet Gausovu krivu, tj. prolazi kroz transformaciju nepromjenjena slicno kao i sto je e^x izvod od e^x.
Tako da inverznom transformacijom od Gausa dobijes opet Gausa. Vjerovatno postoji jednostavan matematicki trik il formulica koji ce frekvenciju da preslika u vreme, odnosno par parametara koji opisuju to preslikavanje, cime bi mogao da izbjegnes FFT i IFFT.
Nadji neku solidnu knjizicu iz oblasti "Signals and Systems" pa prosvrljaj malo kroz teoriju, malo "teorije" moze da te postedi od dosta "prakse".
[ milanche @ 24.04.2010. 07:31 ] @
Bas dobra dosetka, svodi problem na izuzetno prosto resenje.
(...kazu u knjigama na web-u da prolazi kroz transformaciju sa istim shape-om, samo drugim parametrima zvona...)
Mada, nece da skodi za bilo koji sledeci slucaj da ipak zna sta radi i zasto.
[ bdrljaca @ 24.04.2010. 21:17 ] @
Hvala na savetima, tako nesto sam i ja skopcao, s tim sto nisam dovoljno dobro potkovan teorijski 
nista, probacu, pa ako uspem super,a ako ne potrazicu od vas jos koji savet 
pozdrav [ bdrljaca @ 24.04.2010. 21:20 ] @
E da, ja sam spreman da idem i na časove kod nekog od vas ako je voljan da mi bude učitelj, ili ako znate nekog ko bi bio bio voljan, javite mi, pa da se čujemo i dogovorimo oko detalja i naravno cene.
pozdrav
[ Odin D. @ 24.04.2010. 22:00 ] @
Ja ti nazalost ne mogu biti ucitelj jer nisam toliko kompetentan za DSP. Pamtim mali dio od onoga sto sam nekad morao znati da bih polozio, i poneku jednostavniju sitnicu ako mi danas-sutra zatreba u neke prakticne svrhe.
Mada, ako bi tacno opisao sta ti treba tj. sta hoces da postignes mozda bih mogao da ti preporucim neku knjigu za koju znam da je ok ili da ti ovdje pomognem u nekim pocetnickim stvarima ako krenes sam da izucavas tu materiju.
[ milanche @ 25.04.2010. 03:54 ] @
Ja mogu da kazem posle svih ovih godina da sam dosta verziran u DSP, razumem stvari dosta dobro u fundamentu,
i gotovo sve sto znam mogu da jasno i jezgrovito objasnim. Privatno sam zaljubljenik u DSP, mislim da je to najcarobnija
grana inzenjeringa (to i system control theory), uzivanje za mozak kad sebi objasnis neke stvari a jos vise kad napises
program koji to nesto radi.
Da ti drzim formalne casove - nemam vremena, a i ne bih to radio za pare.
U Srbiji trenutno ne znam koga da ti preporucim za tako nesto osim usual suspects - profesora na ETF-u.
Ono sto hocu i verovatno mogu (koliko mi vreme dozvoljava) je da ti
a) dam pravi putokaz, sta da trazis po knjigama i na web-u
b) objasnim precizno i na prostom srpskom jeziku bitne koncepte, posle kojih ces formule da razumes i pamtis znatno
lakse.
[ maza1 @ 25.04.2010. 14:04 ] @
Milanche, svaka chast na znanju. Pitanje ove teme mi je bilo interesantno, ali nisam imao nista pametno da kazem. Sad imam malo tematike za razmisljanje, hvala!
[ bdrljaca @ 25.04.2010. 19:01 ] @
Meni bi najbolje bilo da se vidim sa nekim, da mu u četiri oka objasnim u čemu je problem, da ponesem i jednačine koje treba numerički da se reše i sve što ide uz njih. Ako niko nije u mogućnosti ne bi bilo loše i da mi preporučite neke knjige i gde bih mogao da ih nabavim. Što se tiče nekog sa ETF-a i to mi je padalo napamet, ali mi se čini malo teže ostvarljivo.
Ništa, ponuda i dalje ostaje, pa ako ima nekog da mi pomogne slobodno nek se javi, a u međuvremenu šaljite literaturu  [ Odin D. @ 25.04.2010. 20:22 ] @
Ne postoji "univerzalna" literatura.
Razlicite knjige pokrivaju razlicite djelove problematike i do razlicite dubine.
Zato sam ti i predlozio da tacno opises sta je problem i sta zelis da postignes.
Jeli to neki jednokratni zadatak koji bi nekako da rjesis i dalje te nista ne zanima?
Jesi li naumio da se inace bavis DSP-om?
Daj da vidimo zadatak konkretno.
Jesi li apsolutni pocetnik ili vec nesto znas? i tome slicne stvari.
Tesko da ti sa ovom kolicinom informacija neko moze nesto ciljano preporuciti, osim onoga sto i sam mozes izguglati na amazonu kucajuci DSP u polje za pretragu.
[ sinisa_s @ 25.04.2010. 21:54 ] @
Ne poznajem srpsku literaturu za DSP ali evo jedan link za jednu besplatnu knjigu iz DSP-a (na engleskom), koja je po mom misljenju lepo napisana i razumljiva za pocetnike. Sva poglavlja se mogu skinuti u pdf formatu. Dosta toga se moze naci besplatno na net-u, pa verujem i literature na srpskom. Predpostavljam da ima i besplatnog softvera, zanimljivog za pocetnike, gde se mogu posmatrati oblici signala pri razlicitim transformacijama. Mnogo se brze razumeju neke stvari ako se nesto i slikovito moze videti.
http://www.dspguide.com/
Pozdrav. [ milanche @ 25.04.2010. 22:20 ] @
Pogledao sam knjigu sa linka koji ti je ostavio sinisa_s.
Izuzetno mi se svidja redosled i raspored podnaslova i lekcija, to bi verovatno bio (uz par manjih dodataka)
redosled lekcija koje bih ti i ja preporucio.
Primetio sam i neke nedostatke knjige:
- ima izuzetno malo konkretne matematike, vise nekih opisnih inzenjerskih diskusija pristojnog kvaliteta.
- neki detalji diskusija nisu udarili na sustinu stvari. U prakticnom zivotu DSP inzenjer nosi u glavi neki odredjen
broj brzih i tacnih principa koji ga lako vode dalje - ovde ti principi nisu podcrtani jasno.
- neke lekcije na koje se trosi nekada gro semestra (Z-transformacija recimo i svi trikovi vezani za nju) su
predjene sa isto prostora kao i neke manje znacajne teme.
Ipak - preporucio bih ti da knjigu sa linka uzmes kao polaznu tacku, tj. nesto kao dobar orjentir za ucenje,
ili ako hoces, spisak ispitnih pitanja.
Pomiri se sa time da ce samostalno ucenje cak i uz nasu prijateljsku pomoc da ti uzme najmanje godinu dana.
Na dobrim univerzitetima uz 4 casa nedeljeno predavanja i redovne nedeljne domace zadatke gigantskog obima,
moze i jedan semestar.
Najteza stvar u DSP-u (a i inace) je ona prva polovina recenice iz klasicne dilema Paje Patka - "a cemu ovo sluzi ?",
tj. "kome je ovo trebalo i zasto ?". Matematiku i objasnjenja ces uspevati da progutas, ali odgovore na ova prosta
pitanja ces samostalno dobijati tek nekoliko godina posle, najvise zato sto ih retko daju u ocitoj formi.
Na bazi podnaslova koje budes sledio u ovoj knjizi, obavezno obidji web da nadjes konkretne formule, domace
zadatke, Matlab skripte i slicno. Imas citavo mnostvo univerziteta na cijim online sajtovima mozes da nadjes
vredne stvari - Columbia University, MIT, Stanford (narocito predmeti koje drzi Julius Orion Smith, sef kompjuterske
laboratorije za muziku CCRMA), itd...
Mozda bi mogao da se ispruzis pa da nabavis neki od klasicnih DSP udzbenika - Prolakis & Manolakis ("Digital Signal
Processing"), Oppenheim & Shaffer ("Digital Signal Processing"), itd. Mogu da se kladim u kintu da s obzirom koliko
su davno pisane da mozes sigurno da ih nadjes negde u PDF formatu za dz.
Od nasih na srpskom imas knjige od Miodraga Popovica (genijalan tip, knjigu nisam imao prilike da vidim) kao i od
Zorana Dobrosavljevica (moja generacija, jedan od najpametnijih ljudi u generaciji, recit, promucuran, bistar kao pcelica,
knjigu nisam citao, ali ocekujem da je fenomenalna).
[ Odin D. @ 26.04.2010. 02:09 ] @
Hm, evo i moje skromno misljenje...
Knjigu koju je @sinisa_s predlozio mogu da preporucim za pocetak, kao neki uvod u razumijevanje problematike. To je knjiga orjentisana na prakticnu primjenu i razjasnjavanje nekih osnovnih stvari na slikovit nacin, te na sticanje neke grube slike o svemu. Nece te odvesti u ko zna kakve dubine, ali u startu se i ne treba zamlacivati kompleksnim detaljima nego opstim razumijevanjem, tako da je manje-vise idealna za start.
Link na tu istu knjigu sam i ja okacio na forumu Mikrokontroleri prije x-vremena kad sam naletio na nju tragajuci za nekim osciloskopima na netu, pa neki od proizvodjaca imao link ka tom stivu.
Imam knjigu od M. Popovica "Digitalna obrada signala" i od Z. Djurovica "Signali i sistemi".
Ova od Popovica obradjuje samo digitalne signale, od Djurovica i digitalne i kontinualne.
Ovu od Popovica sam citao, a od Djurovica pomalo prelistavao, kad zatreba.
Sve su to dobre knjige i u principu sadrze mnogo vise materije nego dvostruko deblje knjige nekih stranaca.
Medjutim, to su knjige namjenski pisane za studentariju, a ne za samostalno proucavanje.
Sta to znaci?
Pa to znaci da se autori nisu narocito osvrtali na to kako bi to sve izgledalo kad bi neki potencijalni citalac sam sebi to morao da razjasnjava.
Pri tom se u tim knjigama poprilicno oslanjaju na radove svojih kolega matematicara i njihovih knjiga za koje pretpostavljaju da je student sve uspjesno savladao i naravno savrseno popamtio u prethodnim semestrima.
Tako npr. mozes procitati:
Mnogo jednostavniji nacin izracunavanja inverzne z-transformacije dobija se primjenom Kosijeve teoreme ostataka, poznate iz analize funkcija kompleksne promenjive. Ako se podintegralna funkcija napise u obliku
pa tras neka kobasica
gdje je k ceo broj koji oznacava broj razlicitih polova funkcije @#$$%, dok celi broj mi oznacava multiplicitet pola pi. Primenom Kosijeve teoreme, iz (xxx) i (xxx) se dobija
pa opet neka kobasica
gdje se ostatak u polu odredjuje formulom:
onda nije vise ni kobasica nego svinjska polutka
ako je pol prost, ili sa............
I tako dalje. Sta to znaci u praksi? Pa ako nisi diplomirao matematiku, to znaci da ces morati kupiti jos i buljuk knjiga iz matematike da bi mogao da "citas sa razumijevanjem".
Ovakvo oslanjanje na predznanje citaoca nisam bas cesto sretao u stranim knjigama. A ako i jesam, onda obicno ima neki matematicki dodatak ili par poglavlja koja razjasne matematiku koja se u knjizi upotrebljava pa onda dalje.
Zatim, pri tom je to pisano bez aspiracija da to postane neki komercijalni hit za sire narodne mase, vec su musterije uglavnom studenti koji slusaju doticni predmet kod doticnog autora, tako da se ne primjecuje preveliki trud u obradi sadrzaja.
Nije da kazem da knjiga ne valja, daleko od toga, ali za pocetak su bolje neke druge.
Za Djurovicevu ne mogu da kazem mnogo, jer je nisam citao redom, nego pomalo i na brzinu kad mi nesto zatreba.
Formula ima dosta, a slika malo sto je nezgodna situacija za pocetnike :(, ali ko zna, mozda mu je tekst slikovit :)
U svakom slucaju, kad bi Djurovic pisao knjige kao sto je drzao vjezbe iz Sistema automatskog upravljanja, bio bi prodavaniji od Harija Pottera.
Da sam ja na tvom mjestu, pod uslovom da nisam neki math-freak koji zna kompletnu tablicu trigonometriskih identiteta napamet, nakon one prvobitno pomenute knjige, koju ces brzo sazvakati, presao bih na neku od onih "klasika" koje je @milance spomenuo. Klasici su ipak klasici, a sve ove druge knjige se manje-vise sklapaju prepisivanjem raznih poglavlja iz raznih klasika....
Pozdrav
[ bdrljaca @ 26.04.2010. 09:03 ] @
Hvala.
Nisam totalni početnik tako da (na sreću) ne moram baš sve da učim od 0. Popovićevu knjigu imam i pročitao sam je, ali sem teorije ne vidim da je u njoj negde rešeno nešto konkretno.
Pitao me je neko da li mi treba za rešavanje jednog prOblema ili planiram da se bavim time u budućnosti. Meni je potrebno konkretno da numerički rešim određenu VREMENSKI-ZAVISNU JEDNAČINU PROTOKA SNAGE, koja ima oblik:
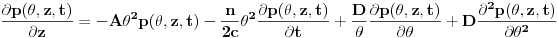
nakon primene Furijeove transformacije, i prelaska u frekventni domen jednačina postaje:
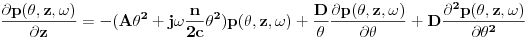
Kako je kompleksno, razdvajamo ga na realni i imaginarni deo, pa dobijamo:
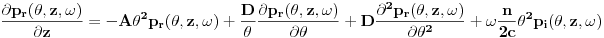
i
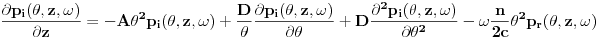
Primenom eksplicitnog metoda konačnih razlika dobijamo dve uparene jednačine:
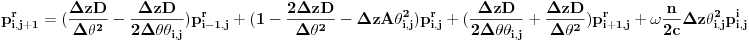
i
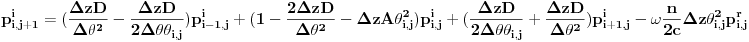
pri čemu postoje i određeni granični uslovi (koji za razumevanje problema nisu mnogo bitni).
Ovo se dalje rešava numerički, pri čemu je upadni snop svetlosti, u vremenskom domenu, u obliku ravanskog talasa dat pomoću Dirakovog impulsa u vremenu, pod nekim uglom u odnosu na osu vlakna.
Ovo se dalje rešava numerički, pri čemu je upadni snop svetlosti, u vremenskom domenu, u obliku ravanskog talasa dat pomoću Dirakovog impulsa u vremenu, pod nekim uglom u odnosu na osu vlakna.
Mene, kao prvo, zanima kako će ulazni impuls izgledati u ferkventnom domenu, i kako ga implementirati na početku vlakna prilikom programiranja i kako na osnovu gore pomenutog izračunati frekventni odziv.
[ Odin D. @ 26.04.2010. 09:35 ] @
Diskretan Dirakov impuls ima kontinualan spektar, tj. nakon Furijeove transformacije postaje 1. Obicna konstanta u frekventnom domenu.
[ ac1bd4 @ 26.04.2010. 11:33 ] @
Ako imaš vremena i volje možeš da pratiš predavanja i vežbe na ETFu. Niko te neće ni pitati da li studiraš ili ne. Možeš i profesora i asistenta na pauzama da pitaš za neke konkretne probleme, a možeš i na konsultacije da ideš. Jedino ne možeš na lab vežbe. Te predmete drži katedra za signale i sisteme i ima više verzija kurseva u zavisnosti od odseka na kom se drže. Najobimniji su naravno kursevi za odsek signali i sistemi. [ bdrljaca @ 26.04.2010. 13:51 ] @
@Odin
Znam da je Fourierova transformacija od Delta impulsa 1, ali šta to znači konkretno znači u mom slučaju? Meni se u jednačini javlja  i ja nisam siguran koje vrednosti za to  da uzmem. Da li  ima vrednosti od 0 pa do reda veličine GHz ili ne, i ako ne koje su vrednosti za  ? [ milanche @ 26.04.2010. 15:27 ] @
Citat: @Odin
Znam da je Fourierova transformacija od Delta impulsa 1, ali šta to znači konkretno znači u mom slučaju? Meni se u jednačini javlja  i ja nisam siguran koje vrednosti za to  da uzmem. Da li  ima vrednosti od 0 pa do reda veličine GHz ili ne, i ako ne koje su vrednosti za  ?
U digitalnoj obradi signala se implicitno podrazumeva da su frekvencije u opsegu izmedju 0 i pola ucestanosti semplovanja.
Cak i ako originalni signal ima vise spektralne komponente, ogranicenja procesa semplovanja cine to da signal posle semplovanje
ne moze imati ni jednu spektralnu komponentu na ucestanosti visoj od Fs/2.
Obicno se podrazumeva, takodje, da je ili Fs odabrano tako da Fs/2 bude vise od najvise frekvencije spektralnih komponenti signala,
ili se signal predhodno pusti kroz tzv. anti-aliasing low pass filter da se uklone sve spektralne komponente na ucestanostima vecim
od Fs/2.
E, sad ti vidi u tome sto radis kolika ti ucestanost semplovanja treba, pa onda radi sa  izmedju 0 i Fs/2.
[ Odin D. @ 26.04.2010. 15:31 ] @
Sto se tice Dirakovog impulsa u frekventnom domenu, on je konstanta, tj. uopste ne ovisi o w. Isto kao sto trojka u jednacini y = 2t + 3 nije nista do konstanta u vremenskom domenu, 3 je uvijek 3 bez obzira koliko sati bilo. E tako isto u vremenskom domenu, Dirakov impuls je 1, na svakoj frekvenciji, tj. za svako w.
Kad si prebacio sistem u frekventni domen, to w ti je nezavisna promjenjiva po kojoj rjesis sistem, kao sto bi ga rjesavao u vremenskom domenu po t.
Kad dobijes rjesenje, to ce u opstem slucaju biti neka funkcija koja zavisi od w. Kad to rjesenje (funkciju od w) inverznom transformacijom prebacis u vremenski domen dobices funkciju koja zavisi od t.
U numericko rjesavanje diferencijalnih jednacina se ne razumijem. Pretpostavljam da to w prosetas po opegu koji tvoj sistem propusta. Ne treba sigurno da ides do 20 GHz ako je propusni opseg npr. do 5 GHz. Zbog tacnosti rezultata i brzine simulacije bitno je da dobro procjenis sa kolikim korakom ces prolaziti kroz to w. Ako uzmes npr. 10Hz mozes dobiti rezultate za djelic sekunde ali neprecizne, a ako uzmes korak od 0.0001 Hz mozes dobiti tacnost od 99.999% a da racunar zvace jednacinu pola dana. To ne mogu ovako napamet da ocjenim, probaj pa vidi sta se desava. U algoritam racunanja ubaci da na svakih xxx koraka napise neku poruku na ekranu, pa vidi koliko brzo se ispisuju. Ako krene suvise sporo onda povecaj korak za w i obratno.
Dalje, sta to u realnosti znaci da opalis Dirakov impuls u opticko vlakno? Pa to fizicki znaci da si mi odjednom na ulaz gurnuo impuls svjetlosti svih mogucih frekvencija. Ono sto izadje na drugom kraju optickog vlakna ce biti svjetlost samo onih frekvencija koje to opticko vlakno propusta, tj. mjerenjem odziva na Dirakov impuls ustvari mjeris propusni opseg vlakna (frekvencijsku karakteristiku).
Probaj da stavis da je Dirakov impuls =1 pa vidi sta dobijas nakon simulacije.
edit: vidim da se u medjuvremenu pominjalo semplovanje, pa da se osvrnem
Koliko vidim, tebi je potrebno da pronadjes kako se prenos snage odigrava duz vlakna (z) u toku vremena (t) u zavisnosti od toga pod kojim je uglom (Theta) uletio impuls svjetlosti u njega.
Posto se u ovom slucaju radi o Dirakovom impulsu, on se ne moze semplovati, odnosno proces semplovanja nema fizicki smisao u ovom eksperimentu. Vozi w do one frekvencije dok ne vidis da dalje nema (znacajnog) uticaja na konacan rezultat.
[Ovu poruku je menjao Odin D. dana 26.04.2010. u 16:44 GMT+1]
[ bdrljaca @ 26.04.2010. 16:48 ] @
Ja sam intuitivno do sad uradio sve što mi predlažete, ali nikako da dobijem dobar rezultat  . Puštao sam do opsega koji mi propušta vlakno-znači so oko 1Ghz. Postoji mogućnost da sam išao sa isuviše velikim korakom semplovanja, s tim da ne znam da li to utiče i na rezultat ili samo na "glatkoću" dobijene krive za frekventni odziv. Osim toga, pošto se radi o frekventno-prostornoj zavisnosti (ili vremensko-prostornoj) ne znam da li redosled operacija utiče na rezultat. Po meni ne, ali, opet kažem nikad nisam radio pa ne znam sa 100% tačnošću. [ milanche @ 28.04.2010. 07:19 ] @
Hajde da probamo da mozgamo zajedno naglas:
Propusni opseg kabla = [0 - 1GHz].
Ucestanost semplovanja u vremenskom domenu bi trebalo da je Fs = 2GHz. To znaci da je period
semplovanja Ts = 1/2GHz = 0.0000000005 sec.
Odluci se za parametre svoje Gausove krive (srednja vrednost m, std devijacija sigma).
Kriva za koju se tako odlucis opisuje zakonomernost po kojoj se menja spektar signala, zbog cega
je za ocekivati je da je srednja vrednost m = 0.
Evo ga izvodjenje http://chsfpc5.chem.ncsu.edu/~...n/CH795Z/math/ft/gaussian.html koje pokazuje
kako Gausova kriva u frekventnom domenu biva transformisana u Gausovu krivu u vremenskom domenu.
Kako odabrati korak semplovanja u frekventnom domenu ?
Zamisli da vec na neki volsebni nacin (recimo, poslao ti brat od strica) imas krivu u vremenskom domenu
koja predstavlja inverznu Furijeovu transformaciju tvoje pocetne Gausove krive. Ta kriva ce od neke tacke
X0 spasti na nulu.
E, sada - rekli smo da je vremenski signal semplovan sa 2GHz (tj. period semplovanja Ts = 0.0000000005 sec).
Tvoja tacka X0 = N*Ts.
Pronadji koliko je to N. Posto posle tog N vremenski signal Gausove krive pada na nulu, ne treba ti vise od
N tacaka. Da bi sebi olaksao zivot, uzmi ne bas tacnu vrednost na kojoj signal pada na nulu, nego prvu vecu
numericku vrednost koja je 2^nesto (512, 1024, 2048, 4096...) - bice ti lakse da uradis inverznu FFT.
Ako pogledas jedan od mojih ranijih postova na ovu istu temu, objasnio sam ti u kakvoj su vezi kolekcija od
N semplova u vremenskom domenu i korak semplovanja u frekventnom domenu.
Da ponovim: ako uzmes N semplova u vremenskom domenu i izracunas FFT, dobijas kolekciju semplova spektralne
krive na rastojanjima k*N/Fs. Vazi i obratno - ako spektralnu funkciju racunas u tackama k*N/Fs, i izracunas
inverznu FFT, dobices N semplova u vremenskom domenu.
Dakle - pronasli smo korak semplovanja u frekventnom domenu, vrednost mu je N/Fs.
Sve sto dalje treba je inverzna furijeova transformacija, i dobio si vremenski signal koji ti treba.
[ Odin D. @ 28.04.2010. 19:38 ] @
Ja samo usput da se ubacim sa jednim potpitanjem:
Naime, a zasto se uopste ta diferencijalna jednaciona rjesava na taj nacin, mislim Furijevom transformacijom?
Ne bi li bilo logicnije da se koristi Z-transformacija?
[ milanche @ 30.04.2010. 06:33 ] @
Citat: Ja samo usput da se ubacim sa jednim potpitanjem:
Naime, a zasto se uopste ta diferencijalna jednaciona rjesava na taj nacin, mislim Furijevom transformacijom?
Ne bi li bilo logicnije da se koristi Z-transformacija?
Moram da se ogradim u jednom smislu - jos uvek razmisljam o problemu u domenu jedne dimenzije, i na bazi
skolskog iskustva sa 2D se sve nadam da se problem u 3D svodi na slican rezon.
Cela prica je krenula od verbalno formulisanog problema (data je spektralna funkcija, kako kreirati signal u
vremenu). Diferencnu jednacinu sam video tek na kraju.
U principu, spektar (analiticka funkcija, tj. Gausova raspodela) ocito konvergira, znaci ne treba petljati
e (sigma + jw) u celu pricu, pa ne vidim da nam treba ni z-transformacija.
U ovom posebnom slucaju gde su spektar i vremenska funkcija iz iste porodice funkcija samo drugacijih
parametara, ne treba nam cak ni konkretno izvrsavanje Fourier-a, samo nam od cele price treba samo
znanje relacija koje donosi poznavanje teorije.
Da li bi resenje preko z-transformacije bilo jednostavnije u ovom konkretnom slucaju - pojma nemam napamet.
Jednostavno, sva iskustva sa z-transformacijom su mi u sasvim drugim scenarijima - recimo: redjas nule i polove
po z ravni, pa racunas frekventnu karakteristiku da vidis kakav bi filter dobio.
U svakom slucaju, ako ne zna z-transformaciju, da mu je objasnim lepo i smisleno, tj. cemu tacno to sluzi, uvek
bih pre posao od Furijeove transformacije.
Ako te ne mrzi, isteraj do kraja resenje preko z-transformacije za ovaj slucaj.
[ Odin D. @ 30.04.2010. 08:25 ] @
Hm, nisam siguran da bih to mogao, a da se opet ne dohvatim knjige...
Pravo da ti kazem, nisam siguran ni da moje pitanje ima mnogo veze sa mozgom.
Znam da je Z-transformacija u diskretnom domenu neki ekvivalent Laplasove u kontinualnom.
Pa kad se laplasovom rjesavaju diferencijalne jednacine u kontinualnom, rekoh vjerovatno bi moglo i z-transformacijom u diskretnom.
Mada, uopste nemam predstavu ovako napamet koliko to moze da korespondira direktno sa ovim slucajem.
U svakom slucaju, moglo bi se sa onim jednacinama koje je dao par poruka ranije krenuti sa pisanjem programa, pa vidjeti gdje ce ga to dovesti.
Vjerovatno bi se u toku implementacije pojavilo neko svjetlo na kraju tunela.
Jos jedno pitanja za @bdrljaca: Sta je ono D u jednacinama?
[ bdrljaca @ 30.04.2010. 09:41 ] @
Evo i mene ponovo, bio sam odsutan par dana.
Hvala na informacijama, za sad su dobrodošle.
U principu mogla je da ide i Laplaceova ili možda i Z, ali meni služi samo da "uprostim" jednačinu, tako da po mom nema razlike. Čini mi se da se čak i Laplaceova u ovom slučaju svodi na Four.
[ milanche @ 30.04.2010. 11:58 ] @
Citat: Pravo da ti kazem, nisam siguran ni da moje pitanje ima mnogo veze sa mozgom
Ja sam siguran da ima.
z-transformacija je samo jedno zgodnije vidjenje Fourier-ove transformacije u kojoj je nepregledna
frekventna osa smotana u krug sa periodom koji odgovara frekvencijama od 0 - Fs/2. Ako se racuna
z-transformacija na jedinicnom krugu, dobijes nista drugo nego vrednosti Furijeove transformacije.
Siguran sam da postoje scenarija u kojima se preko z-transformacije dodje do znatno preglednijih
rezultata, jedino sto mi ovaj scenario ne lici na jedan od tih.
Pitao sam jednog kolegu koji je pravi opasni DSP covek koji nista drugo zapravo i ne radi u struci
nego DSP - kaze da sve varira od slucaja do slucaja i da uvek treba pokusati oba pristupa pa videti
gde ispada jeftinije za mozak i za masinu (najbolje za oba).
Citat: Čini mi se da se čak i Laplaceova u ovom slučaju svodi na Four.
Laplasova je samo prosirenje Fourier-ove za slucajeve signala cija Fourier-ova transformacija ne
konvergira, pa se umesto e jomega radi sa e sigma + jomega gde se za bar neke vrednosti
sigma dobija zadovoljavajuci uslov. Za signal koji ti je zadat (data ti je funkcija u frekventnom
domenu koja je konacna za svako omega), Laplasova je verovatno izlisna.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|