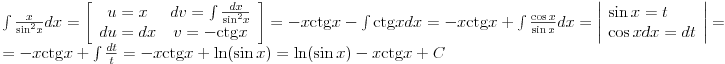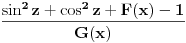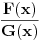[ R A V E N @ 01.05.2010. 13:03 ] @
Kako glasi riješenje integrala ?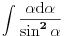

Na S.O.S. MATHematics je data ova opšta formula za riješavanje integrala ovog tipa, a ovo je slika direktno sa te stranice: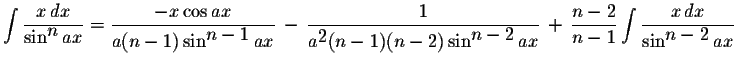


.

No, očigledno je da postoji problem sa tom formulom za 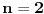, jer se u drugom sabirku dobiva ispod razlomačke crte.

Unošenje integrala u kalkulator integrala na http://www.numberempire.com/integralcalculator.php daje ovaj prilično kompleksan izraz: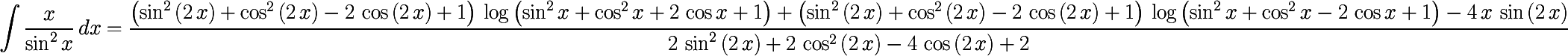



koji se sigurno može pojednostaviti, no prije nego što to probam, htio bih da vidim riješenje integrala. Stvar je u tome da mi to treba za riješenje zadatka iz elektromagnetizma (jačinu električnog polja), a očigledno da tako kompleksan izraz ne ide u izraz za .

[Ovu poruku je menjao R A V E N dana 01.05.2010. u 14:44 GMT+1]
[ igorpet @ 01.05.2010. 15:48 ] @
[ R A V E N @ 01.05.2010. 16:48 ] @
Hvala. Pretpostavljam da je formula sa S.O.S. MATHematicsa netačna?
[ Cabo @ 02.05.2010. 16:51 ] @
Onaj tamo kilometarski razlomak je prepun nesvedenih izraza tipa koji se svode na .
[ R A V E N @ 02.05.2010. 17:13 ] @
Već sam prije znao iz knjige da ima u riješenju prirodni logaritam, a kada sam na brzinu pogledao taj izraz, nije ga bilo, tako da i nisam probao da izvršim pojednostavljivanje.



Ustvari ima prirodni logaritam, samo ga oni označavaju sa a ne sa . Dekadski se označava sa .