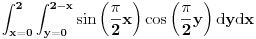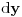[ R A V E N @ 04.05.2010. 03:58 ] @
|
[ danijell @ 04.05.2010. 09:39 ] @
Možda da prvo izraz pod integralom središ koristeći trigonometrijsku formulu
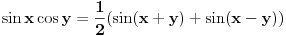 Nakon toga riješiš integral po promjenljivoj y, pa onda po x. Pripaziš na smjene, pa ćeš imati: - skraćivanje dva ista člana različitog predznaka - integral od cosx na [-π,π] - jedan elementarni intergal koji i daje konačni rezultat. A što se tiče smjena kada radiš integral po y , onda x posmatraš kao nepromjenljivu. [ NicholasMetropolis @ 05.05.2010. 12:55 ] @
Citat: R A V E N:Ali kako uvrstiti u to dobiveno riješenje ovu granicu 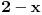 ? ?Ne razumem šta je tu problem 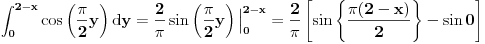 [ Dinaaaa @ 02.06.2010. 19:23 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|