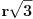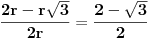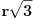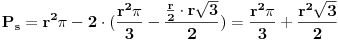|
|
[ zzzz @ 16.01.2004. 01:40 ] @
|
| ako je onaj lagani problem sa tri kutije napatio neke , šta će biti sa ovim?
U ravnini imamo kružnicu koju siječe pravac.Dva puta manja kružnica ima
zajednički centar sa prvom.(D1=2*D2).Kolika je šansa da pravac siječe i ovu
manju?
|
[ -zombie- @ 16.01.2004. 02:10 ] @
ako "pravac" znači "prava", onda bi trebalo da je verovatnoća 50%..
[ srki @ 16.01.2004. 03:18 ] @
Zadatak nije potpun jer nisi rekao kako se bira prava. Da li izaberes jednu tacku pa onda proizvoljan ugao ili biras dve tacke ili na neki treci nacin odredjujes pravu? Resenje nije isto i zavisi od toga kako odredjujes pravu.
[ noviKorisnik @ 16.01.2004. 09:24 ] @
srki, zadatak je određen s tri tačke. Jedna je zajednički centar obe kružnice, a druge dve su presečne tačke veće kružnice s pravom.
Rekao bih da i ovde mogu da se dese dileme oko verovatnoće... Milane, svaka čast!
[ noviKorisnik @ 16.01.2004. 09:49 ] @
Za početak, da se demantujem.
Pomenute tri tačke određuju jednakokraki trougao. Zadatak se može definisati na bilo koji način koji jedinstveno određuje jednakokraki trougao.
Granični slučaj zadatka je takav trougao kome je dužina visine nad osnovicom jednaka polovini dužine kraka. Tada je prava tangenta manje kružnice. Takav trougao naziva se još jednakostranični.
Ako se verovatnoća određuje u odnosu na veličinu ugla naspramnog osnovici jednakokrakog trougla, tada je verovatnoća da prava seče manju kružnicu 2/3.
Ako se verovatnoća određuje u odnosu na rastojanje centra kruga od prave, relativno na poluprečnik veće kružnice, tada je verovatnoća da prava seče manju kružnicu 1/2.
[ noviKorisnik @ 16.01.2004. 11:36 ] @
Demantima nikad kraja Citat: Granični slučaj zadatka je takav trougao kome je dužina visine nad osnovicom jednaka polovini dužine kraka. Tada je prava tangenta manje kružnice. Takav trougao naziva se još jednakostranični. Naravno da nije jednakostranični. Pobrkah neke sinuse i kosinuse.
Takav trougao ima ugao od 2/3 pi. Kod trouglova koji imaju uglao veći od ovoga dolazi do sečenja manje kružnice, kod ostalih ne.
Iz prethodne greške sledi i sledeća Citat: Ako se verovatnoća određuje u odnosu na veličinu ugla naspramnog osnovici jednakokrakog trougla, tada je verovatnoća da prava seče manju kružnicu 2/3. Ispravno je da je ova verovatnoća 1/3.
Sve ove verovatnoće su relativne u odnosu na nešto. Recimo:
Ugao između kraka i osnovice treba da je manji od 1/6 pi da bi se desilo sečenje manje kružnice. Po kriterijumu ovog ugla verovatnoća iznosi 1/6.
[ gpreda @ 16.01.2004. 13:52 ] @
Zadatak je lepo postavljen - u ravni su date dve koncentricne kruznice i prava. Kada se resava treba imati u vidu metode kojima se racuna geometrijska verovatnoca. Dacu vam jedan primer kako se moze lako pogresiti u ovakvim zadacima.
zadatak: Dat je krug poluprecnika R, i na njemu je izabrana proizvoljna tetiva AB. Kolika je verovatnoca da je duzina tetive veca od duzine stranice jednakostanicnog trougla upisaonog u taj krug?
resenje 1: Duzina tetive je u potpunosti odredjena udaljenoscu njene sredine od centra kruga. Tetiva je duza od stranice jednakostranicnog trougla ako se njena sredina nalazi na udaljenosti manjoj od R/2 od centra kruga. Verovatnoca da se to desi je povrsina_malog_kruga / povrsina_kruga
=> P = 1/4
resenje 2: Nacrtajmo unutar kruga jednakostranicni trougao AB'B'' . Jasno je da je duzina tetive AB duza od stranice jednakostranicnog trougla akko se B nalazi na luku B'B''. Verovatnoca da se to desi jeste duzina_luka_B'B'' / obim_kruga
=> P = 1/3
Sta mislite koje resenje je korektno?
[ noviKorisnik @ 16.01.2004. 14:06 ] @
I to je opet isti taj zadatak, samo što smo dobili još kriterijuma po kome određujemo verovatnoću i jedan novi rezultat: 1/4.
Koje resenje je korektno? Ne znam koje su to metode kojima se računa geometrijska verovatnoća. Ako neko od ponuđenih rešenja nije rađeno korektnim metodom, onda "verovatno" ni rešenje nije korektno.
Nešto više o metodama?
[ srki @ 16.01.2004. 14:33 ] @
Pa svako resenje je tacno u zavisnosti od toga kako se odredjuje tetiva. Zato sam pitao Milana na koji nacin odredjuje polozaj prave jer bez toga ne moze da se resi zadatak.
[ gpreda @ 16.01.2004. 14:56 ] @
Ponavljam ponovo - pocetni zadatak je lepo postavljen. "Zadata je prava u ravni", znaci da su svi moguci slucajevi podjednako verovatni. Svaka prava je odredjena sa dve svoje tacke, pa moze da se u zadatku kaze "izabrane su dve proizvoljne tacke u ravni" i opet ce se dobiti isto.
Ne mogu postojati dva korektna resenja zadatka koji sam postavio, to bi bio paradoks. Ako se u zadatku kaze "proizvoljna tetiva na krugu" time je potpuno odredjen zadatak i jedinstvenost resenja. Jedno resenje je definitivno pogresno.
[ noviKorisnik @ 16.01.2004. 15:15 ] @
Nedostaje samo definicija verovatnoće...
[ srki @ 16.01.2004. 16:18 ] @
Citat: gpreda:
Ponavljam ponovo - pocetni zadatak je lepo postavljen. "Zadata je prava u ravni", znaci da su svi moguci slucajevi podjednako verovatni.
Zadatak nije lepo postavljen jer kako god da odredjujemo pravu slucajevi su jednako verovatni. Njihova verovatnoca je 0.
Citat: Svaka prava je odredjena sa dve svoje tacke, pa moze da se u zadatku kaze "izabrane su dve proizvoljne tacke u ravni" i opet ce se dobiti isto. Ne, milan to nije rekao. Mozda je prava odredjena tackom i uglom.
Citat: Ne mogu postojati dva korektna resenja zadatka koji sam postavio, to bi bio paradoks. Ako se u zadatku kaze "proizvoljna tetiva na krugu" time je potpuno odredjen zadatak i jedinstvenost resenja. Jedno resenje je definitivno pogresno.
Ne, nije pogresno jer nisi rekao na koji nacin odredjujes proizvoljnu tetivu na uglu. Bilo koji nacin da izaberes jednaka je verovatnoca za svaki slucaj jer je verovatnoca jednaka nuli. [ BOOK @ 16.01.2004. 16:23 ] @
Ovo je jedan od najpoznatijih zadataka iz teorije verovatnoće. Legendarni profesor MG-a, g. Mališić, je ovaj zadatak rešio na tri načina od kojih svi izgledaju POTPUNO TAČNI, LOGIČNI I BEZ GREŠKE, te tako dobio tri potpuno različita rešenja.
Na kraju se ispostavilo da nijedno nije bilo tačno - već jedno sasvim levo, četvrto rešenje!! Toliko o verovatnoći.
Inače, nemam sad vremena da pišem pravo rešenje ovog zadatka (premala mi margina ;).
[ -zombie- @ 16.01.2004. 16:34 ] @
da li to slučajno ima nekakve veze sa onim (paradoksalnim) dokazom da realnih brojeva u intervalu [0, 1] ima isto koliko i u intervalu [0, +beskonačno)
(izvinjavam se što ne znam tex ;)
[ srki @ 16.01.2004. 17:00 ] @
Citat: BOOK:
Ovo je jedan od najpoznatijih zadataka iz teorije verovatnoće. Legendarni profesor MG-a, g. Mališić
On je legenda. Kada sam mu resio jedan zadatak u 4-5 koraka za koji je njemu otislo pola casa onda se odusevio pa posle nisam morao da radim pismene i kontrolne...
Zaboravio sam tacno kako glasi zadatak ali znam da sam razmisljao u nekom smeru kako niko normalan ne bi razmisljao. On je kao i vecina njih pravio neke tabele pa sabirao iterativno itd...bio je zeznut zadatak.
A kod njega na pismenim i kontrolnim je bilo ovako. Zada 5 zadataka uzasno teskih i najbolje sto neko uradi je da ima 2 zadatka i taj dobije dve petice. Oni koji imaju 1 i po zadatak dobiju 5, oni koji imaju 1 zadatak dobiju 4, ko ima pola zadatka dobije 3 a dovoljno je da resis neki mali deo nekog zadatka za 2.
[ zzzz @ 16.01.2004. 17:05 ] @
Citat: BOOK:
Ovo je jedan od najpoznatijih zadataka iz teorije verovatnoće. Legendarni profesor MG-a, g. Mališić, je ovaj zadatak rešio na tri načina od kojih svi izgledaju POTPUNO TAČNI, LOGIČNI I BEZ GREŠKE, te tako dobio tri potpuno različita rešenja.
Na kraju se ispostavilo da nijedno nije bilo tačno - već jedno sasvim levo, četvrto rešenje!! Toliko o verovatnoći.
Mislim da je ovo malo starije od g.Mališića.
Inače mislim da diskusija teče u ispravnom smjeru.Dakle zadatak se rješava sa diskusijom.Srki je pretjerao sa onim p=0.(neka homogena distribucija se mora uvažiti!)
-(Naprimjer dvije slučajne tačke u velikom krugu.Možda je bar jedna i u manjem,a
možda nijedna,ali ih "zaklanja" manji krug.)
-Osim prave i one dvije kružnice , neku ulogu igra i ravan (Euklidska naravno).
[ srki @ 16.01.2004. 17:28 ] @
Citat: zzzz:
Inače mislim da diskusija teče u ispravnom smjeru.Dakle zadatak se rješava sa diskusijom.Srki je pretjerao sa onim p=0.(neka homogena distribucija se mora uvažiti!)
Nisam preterao. To sto sam napisao je potpuno tacno. Moja homogena distribucija moze da bude razlicita od tudje homogene distribucije. Ali verovatnoca da se prava nadje u tacno odredjenom polozaju je 0 za bilo koji slucaj polozaja prave.
Verovatnoca je homogena u drugom smislu.
Ja recimo kada biram tacku u ravni to biram na homogen nacin (znaci ista povrsina ima istu verovatnocu da se u toj povrsini nadje tacka) ali takodje isti ugao mi ima istu verovatnocu da prava zauzima pravac u okviru tog ugla. E a ako neko na homogen nacin bira dve tacke to onda nije isto. [ Bojan Basic @ 16.01.2004. 18:41 ] @
Početni zadatak ekvivalentan je onome koji je Goran kasnije postavio. A taj drugi zadatak je čuveni Bertrandov paradoks, o kojem matematičari i danas polemišu, i izgleda da se razumno objašnjenje neće nikad naći.
[ noviKorisnik @ 17.01.2004. 09:01 ] @
Formulisao bih postavku verovatnoće za ovaj zadatak na sledeći način:
- od svih pravih koje seku veću kružnicu, koliko je onih koje istovremeno seku i manju?
Ova postavka opet deluje nedorečeno i prekomplikovano, pa ću preformulisati na nešto jednostavnije a ekvivalentno (što naravno neću dokazivati):
- fiksiramo jednu tačku veće kružnice i posmatramo sve prave koje tu veću kružnicu, koliko od njih istovremeno seku i manju.
Ovo već deluje lakše.
Sve prave koje posmatramo određene su s dve tačke veće kružnice, od kojih je jedna ona lepa fiksirana. To je pramen pravih koji može da se preslika na kružnicu, te dalje posmatramo samo kružnicu. Kružnica je lep skup tačaka koji može dobro da se meri...
Sad malo konstrukcije:
- upišemo u veću kružnicu jednakostaničan trougao koji ima jedno teme u fiksiranoj tački.
Prave kojima pripadaju stranice ovog trougla su tangente manje kružnice. Veća kružnica je temenima trougla podeljena na tri jednaka luka. Svaka tačka kružnog luka naspramnog fiksiranoj tački određuje s fiksiranom tačkom pravu koja istovremeno seče i veću i manju kružnicu. Nijedna prava koju određuju fiksna tačka i tačka iz preostala dva luka ne seče manju kružnicu (ali zato svaka seče veću).
Konačni odgovor na pitanje je: verovatnoća da prava koja seče kružnicu istovremeno seče i koncentričnu kružnicu dva puta manjeg prečnika je 1/3.
[ srki @ 17.01.2004. 11:25 ] @
Citat: noviKorisnik:
Formulisao bih postavku verovatnoće za ovaj zadatak na sledeći način:
- od svih pravih koje seku veću kružnicu, koliko je onih koje istovremeno seku i manju? Prava ima beskonacno mnogo pa zbog toga morad da napises kako odredjujes pravu. Ne mozes da pretpostavis i tako resis zadatak.
Citat: Sve prave koje posmatramo određene su s dve tačke veće kružnice, od kojih je jedna ona lepa fiksirana.
Ali ako ja definisem na drugi nacin dobicu potpuno drugaciju verovatnocu od tebe.
Ako ja posmatram prave odredjene sa jednom tackom na kruznici i uglom od 0-180 dobicu drugacije resenje nego ti.
Zadatak ne moze da se resi ako ne kazes kako se odredjuju te prave jer prave mogu da se odrede na nekoliko nacina.
[ noviKorisnik @ 17.01.2004. 14:39 ] @
Citat: srki:
Ako ja posmatram prave odredjene sa jednom tackom na kruznici i uglom od 0-180 dobicu drugacije resenje nego ti. Neka je ta tačka takva da tangenta kroz nju leži pod uglom od 0 stepeni u odnosu na koordinatni system. Ova prava je jedina koja prolazi kroz tu tačku a ne seče kružnicu, no to i nije bitno.
Prava koja ima vrednost ugla veću od 60 stepeni i istovremeno manju od 120 je prava koja seče manju kružnicu. Ostale prave ne seku manju kružnicu.
Odnos ovako definisanih pravih je opet 1:2, a verovatnoća da prava seče manju kružnicu 1/3.
U čemu je razlika? [ Bojan Basic @ 17.01.2004. 15:21 ] @
Kao što sam rekao radi se o Bertrandovom paradoksu koji već više vekova ima 3 različita rešenja. Matematičari još nisu uspeli da se dogovore, pa ne verujem ni da ćemo mi uspeti.
Rešenje 1:
Ako proizvoljno odaberemo 2 tačke na kružnici, postupamo na sledeći način. Upišemo u kružnicu jednakostranični trougao čije je jedno teme prva izabrana tačka. Posle toga, uslov zadatka je zadovoljen ako je druga tačka na naspramnom luku, a verovatnoća toga je 1/3.
Rešenje 2:
Pravu posmatramo kao tetivu, a tetiva je u potpunosti određena svojom sredinom. Uslov zadatka je zadovoljen ako se ta sredina nalazi u unutrašnjoj kružnici, a verovatnoća toga je 1/4.
Rešenje 3:
Pravu posmatramo kao tetivu, a tetiva je u potpunosti određena svojom sredinom. Uslov zadatka je zadovoljen ako se ta sredina nalazi na udaljenosti od centra između r/2 i r, a verovatnoća toga je 1/2.
Ovo nisam napisao da biste se vi odlučili za jedno rešenje koje smatrate da je tačno, već da pokažem oko čega matematičari još uvek polemišu.
[ marko37 @ 17.01.2004. 17:58 ] @
Iz centra kružnice povučeš normalu na pravu. Imamo duž sa tri tačke na
njoj - krajnje tačke su centar kružnice i tačka na kružnici, a negde na
duži se nalazi i tačka preseka sa pravom. S obzirom da ništa nije rečeno
o odabiru prave, možemo pretpostaviti da je distribucija po duži
uniformna. Koncentrična kružnica sa dva puta manjim poluprečnikom => dva
puta kraća duž. Verovatnoća da se presečna tačka nalazi u toj polovini
duži je 1/2. A to je verovatnoća da prava preseca kružnicu.
--
“1st Rule of Bayonette Fighting: Never get close enough to do it!”
[ noviKorisnik @ 18.01.2004. 00:00 ] @
OK, Bojane, skontao sam Rešenje 2:
Svaka unutrašnja tačka većeg kruga odgovara tačno jednoj pravoj koja seče taj krug. Konstrukcija je jednostavna: spajamo tačku s centrom kruga i normala na tu duž predstavlja odgovarajuću pravu.
1/4 predstavlja meru skupa unutrašnjih tačaka manjeg kruga prema skupu unutrašnjih tačaka većeg kruga.
Citat: Ovo nisam napisao da biste se vi odlučili za jedno rešenje koje smatrate da je tačno, već da pokažem oko čega matematičari još uvek polemišu.
Nisam matematičar, ali to nije razlog da se ne uključim u polemiku ovde, jer postoje elementi koji navode koje bi rešenje moglo da se smatra za ispravno, a koje ne.
U celoj ponudi mi je najlogičniji odgovor za rešenje 2 (znači P = 1/4) bez obzira što sam u prethodnim porukama branio rešenje 1.
Kao prvo, problem vidim kao traženje odgovora na to koji broj pravih seče manji krug od svih pravih koje seku veći.
Možda se cela zabluda svodi na to da se ovde ipak radi o beskonačnim skupovima.
Nastaviću bez obzira na to.
Rešenje 3 odbacujem jer se svodi na raspodelu pravih koje su normala na duž između centra i jedne tačke kružnice.
Rešenje 1 odbacujem jer se svodi na raspodelu snopa pravih kroz jednu tačku kružnice.
Oba ova rešenja rade analizu na nekom podskupu skupa pravih, dok Rešenje 2 posmatra ceo skup pravih koji seče veću kružnicu.
Za kraj bi bilo lepo da nekim dokazom oborim Rešenje 1 i 3, ali to se neće desiti - kao što rekoh - nisam matematičar. [ Bojan Basic @ 18.01.2004. 01:25 ] @
Citat: noviKorisnik:
Citat: Ovo nisam napisao da biste se vi odlučili za jedno rešenje koje smatrate da je tačno, već da pokažem oko čega matematičari još uvek polemišu.
Nisam matematičar, ali to nije razlog da se ne uključim u polemiku ovde
Ovde si me pogrešno shvatio, kada sam rekao "matematičari" nisam mislio na nas ovde, već na doktore i predavače na najboljim svetskim univerzitetima, jer oni su predodređeni da rešavaju otvorene probleme, zaista je nerealno očekivati da će neko odavde to sada da uradi (možda kasnije u životu).
Citat: Možda se cela zabluda svodi na to da se ovde ipak radi o beskonačnim skupovima.
Naravno, tu si u pravu, to je činjenica.
Citat: Oba ova rešenja rade analizu na nekom podskupu skupa pravih, dok Rešenje 2 posmatra ceo skup pravih koji seče veću kružnicu.
To jeste tačno, ali mnogi zadaci iz verovatnoće se rešavaju svođenjem na prostiji slučaj, pa ne vidim zašto bi ovo bio izuzetak. Hoću da kažem, mi uzimamo snop pravih kroz jednu tačku kružnice, ali to može biti bilo koja tačka kružnice, pa time ne umanjujemo opštost, zar ne? Slično u rešenju 3.
Citat: Za kraj bi bilo lepo da nekim dokazom oborim Rešenje 1 i 3, ali to se neće desiti - kao što rekoh - nisam matematičar.
Tu si u pravu, to se neće desiti, ali ne zbog toga što nisi matematičar (mada ja mislim da posećivanjem ovog foruma i učestvovanjem u ovim raspravama dokazuješ suprotno), već zbog toga što su sva tri rešenja tačna, zato se to i zove Bertrandov paradoks. Korektnost različitih rešenja, kao što je naglašeno više puta, potiče zbog različitog načina odabira prave. [ darkosos @ 18.01.2004. 22:59 ] @
Interesantna tematika. Prvo sam pokušao da zamislim najbolji način da se računa ovakva vrsta verovatnoće, pa sam se zakucao :
ako krenemo standardno, dakle da definišemo prostor verovatnoće, pa onda broj mogućih i povoljnih, dolazimo do potrebe da "merimo" neprebrojive skupove (recimo da pravu koja seče kružnicu možemo predstaviti parom tačaka na kružnici). Kada ih merimo standardnom (Lebegovom) merom, dobijamo paradoks, koji je posledica toga da skupovi iste kardinalnosti mogu imati meru od 0 do beskonačno (Kantorov skup i npr. cela realna osa). Dakle ovo definitivno otpada. Pokušao sam da smislim neku smicalicu, ali nisam otišao daleko.
S' druge strane, tu je uvek eksperimentalna verovatnoća, dakle veliki broj ponavljanja. Da li iko može reći da bi u realnom pokusu mogli dobiti ovako različite rezultate, tj. da verovatnoća "divergira"? A ako bi dobili jedan rezultat, koji bi to bio?
[ -zombie- @ 19.01.2004. 00:28 ] @
pokus bi mogao da se izvede prilično lako, čak i sa malim programčetom, ali je problem opet kako "slučajno" odabirati te prave?
ako ih biramo tako što slučajno odabiramo dve tačke, dobijemo jedan rezultat, preko tačke i ugla drugi, a na treći način treći rezultat.
znači, ne bi smo odmakli daleko...
[ Bojan Basic @ 19.01.2004. 00:38 ] @
-zombie-, upravo to bi bilo idealno. Da pomoću 3 različita programa dobijemo tri različita rezultata.
[ darkosos @ 19.01.2004. 08:34 ] @
To je isti pristup kao što je izložen ranije, i naravno da bi dobio iste rezultate kao i računom. Ono što sam ja predložio je bukvalno eksperiment, kao bacanje novčića.
Citat: ali je problem opet kako "slučajno" odabirati te prave?
Kada baciš novčić ko brine o tome kako se slučajno bira strana na koju će pasti?
Ne znam da li znate sledeći eksperiment : bacaju se šibice čije su dužine jednake polovoni širine dasaka poda; količnik broja bačenih šibica i onih koje na podu presecaju pukotinu između dve daske se približava broju pi. [ -zombie- @ 19.01.2004. 14:07 ] @
Citat: darkosos:
Kada baciš novčić ko brine o tome kako se slučajno bira strana na koju će pasti?
pa.. postoji mala razlika između slučajnog odabira događaja sa konačno mnogo ishoda (i to najmanje moguće -- dva), i slučajnog izbora događaja sa em beskonačno mnogo ishoda, em neprebrojivo mnogo ishoda.
dakle, ja sam pričao o programu koji bi slučajno birao prave. za novčić je lako, if (Random()>0.5) then "glava". ako je tako očigledno, daj mi tu formulu za slučajno određivanje prave (ja ti mogu dati tri, ali koja je prava?)
a uz to, ograničava nas i predstavljanje beskonačnih neprebrojivih skupava u računaru..
dakle, ostaje samo ručna metoda, koja ni sama ne garantuje slučajno odabiranje pravih. predlažem ovakvu metodu experimenta: dva učesnika i malo veći papir. jedan iscrta što više random pravih, a drugi nezavisno odredi gde će biti centar krugova, i koliki će biti prečnik. ovaj drugi deo je moguće ponoviti više puta (jer je lakše nacrtati dva kruga nego 50tak pravih ;)
// i još jedan primer problema sa izvođenjem experimenata verovatnoće sa beskonačnim skupovima: ja zamišljam prirodne brojeve. koja je verovatnoća da zamislim broj 42, a koja da zamislim 7326573627541398765481768417? da li su iste? zašto??
[ darkosos @ 19.01.2004. 23:13 ] @
Citat: pa.. postoji mala razlika između slučajnog odabira događaja sa konačno mnogo ishoda (i to najmanje moguće -- dva), i slučajnog izbora događaja sa em beskonačno mnogo ishoda, em neprebrojivo mnogo ishoda.
dakle, ja sam pričao o programu koji bi slučajno birao prave. za novčić je lako, if (Random()>0.5) then "glava". ako je tako očigledno, daj mi tu formulu za slučajno određivanje prave (ja ti mogu dati tri, ali koja je prava?)
Hvala ti. Sada "uviđam" razliku :)
Šalu na stranu, nismo se razumeli. Ja pričam o stvarnom eksperimentu. Evo ispravke, samo za tebe zombi : dakle
kada zaista bacaš novčić, ko brine o tome na koju će stranu pasti?
(Tu ti ne trebaju programi i formule.)
Da si pročitao moj prvi komentar, video bi da mi je više nego jasno s' čim ovde imamo posla.
Što se tiče tvog eksperimenta, mislim da opet ne bi pokazao pravo stanje stvari, jer čovek teško da može da crta "random" prave. Uostalom, tada ne bi postojali Roršahovi testovi i slično...
Rešenje bi bilo "bacanje" pravih. U tom smislu je i bila pomenuta analogija sa novčićem : isti zakoni koji daju verovatnoću za novčić daće i za pravu. I opet : može li neko sumnjati da će i takav experiment dati različite rezultate. Moram priznati da bih se debelo iznenadio kada bi se to pokazalo. Dakle nešto u našem zaključivanju ne valja kada dobijamo različite verovatnoće. Razlog za to sam i naveo u prvoj poruci. Mislim da ne bi bilo teško smisliti način da dobijemo proizvoljnu verovatnoću a da sve izgleda "logično". [ zzzz @ 20.01.2004. 02:48 ] @
Najprije eksperiment:
Vrti se ručica po velikoj kružnici oko njenog centra,a na njoj se opet vrti neka
šipka.To je nešto kao oni moderni ringišpili.Kad sve slučajno stane onda će ona
šipka možda sjeći manju kružnicu.Velikim brojem pokusa dokazali bi da je to 1/3.
Bojan je naveo tri mogućnosti.(1/2;1/3;1/4).Za ostala dva slučaja zasad neću
praviti skalameriju jer sam već ranije pretjerao sa onim patentom terazija.(To je
ono vaganje dukata).
Srki je u pravu , jer se može napraviti i takva distribucija pa da rezultat bude P=0
samo ja nebih znao napraviti mehanizam da to dokaže.(Programski da!)
Podržavam -zombie- koji je odmah dao prijedlog 1/2!
A zašto?Pokušaću objasniti u svom sledećem javljanju.
[ Bojan Basic @ 20.01.2004. 03:34 ] @
Citat: zzzz:
Najprije eksperiment:
Vrti se ručica po velikoj kružnici oko njenog centra,a na njoj se opet vrti neka
šipka.
Bez ikakvih problema prva ručica ni ne mora da se vrti, mada je i ovo tvoje korektno.
[ darkosos @ 20.01.2004. 07:36 ] @
Samo da dodam još jednu moguću interpretaciju :
kolika je verovatnoća da proizvoljna duž, ne duža od 2r, bude duža od 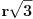 ?
A evo i načina da dobijemo proizvoljnu verovatnoću. Malo ću uprostiti, ali može da se prilagodi i tekućem problemu :)
Date su dve prave u ravni koje se seku u tački A. Obležimo jedan od uglova koji grade sa a. Kolika je verovatnoća da proizvoljno izabrana prava koja prolazi kroz A, upada u a?
Moguće rešenje : opišemo krug oko A i biramo drugu tačku prave na kružnici. Po prethodnoj logici, dobićemo odnos obima kruga i dvostruke dužine luka koji određuje a.
Zamislimo sada da smo umesto kruga izabrali npr. elipsu. Odnos lukova se sada menja. Lako se može zamisliti kako se biranjem različitog odnosa između osa elipse dobija proizvoljna verovatnoća!
//
syntax error ispravljen, thanks to noviKorisnik ;)
[ Ovu poruku je menjao darkosos dana 21.01.2004. u 00:17 GMT] [ noviKorisnik @ 20.01.2004. 08:42 ] @
Citat: kolika je verovatnoća da proizvoljna duž, ne kraća od 2r, bude duža od 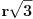 ?
Hajde lepo objasni šta ovo znači. [ darkosos @ 20.01.2004. 14:13 ] @
Probaću nejlepše što mogu :)
Umesto prave koja seče kružnicu, posmatramo samo tetivu koju krug odseca na pravoj. Ta tetiva je dužine najviše 2r.
Sada zaboraviš pravu i gledaš samo tetive, jer je izbor sečice isto što i izbor tetive. Lako se vidi da će tetiva seći manji krug samo ako je dužine veće od 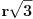 . Tako se zadatak svodi na izbor dužine tetive, bez obzira na položaj. (Možemo zamisliti da smo izabrali neki pravac pravih koje seku kružnicu).
Ako sad ovo prevedemo u brojeve, pitanje je kolika je verovatnoća da slučajan broj u intervalu (0,2r] bude veći od 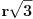 ? Ako bi išli logikom mere (uniformne raspodele), onda je to 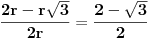 što je poprilično (neočekivano) malo.
[Ovu poruku je menjao Bojan Basic dana 15.05.2005. u 13:00 GMT+1][ noviKorisnik @ 20.01.2004. 14:54 ] @
Darko, hvala na računici. Stoji.
Imao si syntaxerror u delu koji sam citirao i to je ono što me je zbunilo (piše: "ne kraća od 2r").
[ zzzz @ 21.01.2004. 23:44 ] @
Originalan problem je i postavljen sa tetivama i dvije kružnice.Ja sam namjerno
malo zakuvao sa pravima umjesto tetiva.
Darko je fino pokazao da samo one tetive koje su duže od R*(korjen iz 3 sjeku)
manju kružnicu.Pošto tetiva može biti duga od 0 do 2R ispade P=0.134("logično").
Ovo bi se moglo ravnopravno pridružiti onom Bojanovom gdje imamo :P=(0.5;0.33;
0.25).
Prave daju bolji uvid u to šta su područja gomilanja.Uzadatku je namjerno preskočen
način distribucije pravih pa možemo po volji manipulisati.Zato ja navijam za 0.5.
Kad bi precizno opisali distribuciju pravaca onda zadatak nebi više bio to što jest.
Ovako on liči na onaj sa skupovima koji sadrže i samog sebe kao člana.
[ darkosos @ 23.01.2004. 08:08 ] @
Mala analiza prethodne ideje sa dužinom slučajno izabrane tetive.
Nekako nije baš intuitivno da sve dužine imaju jednaku verovatnoću. Ako zamislimo da putujemo po nekom prečniku kruga konstantnom brzinom, onda se dužine tetiva normalnih na tačke koje prolazimo menjaju u skladu sa našim položajem. Praktično su vezane za jednačinu kružnice. Ako ovo zamislimo kao raspodelu verovatnoće, onda se verovatnoća dobija integraljenjem.
U trenutku kada je tetiva dostigla (prvi put) dužinu 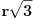 , stigli smo tačno na početak malog kruga (naravno, to je i bila logika računa dužine tetive). Drugi put smo na kraju istog. Dakle, treba da izračunamo površinu u "sredini". Za ovo nam nisu ni potrebni integrali, to bi trebalo i osnovac da zna da uradi - od P celog kruga oduzimamo P delova levo i desno.
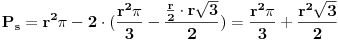
(formule se govorile više od reči :)
Verovatnoća bi tada bila  tj. 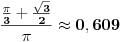
Pa se ti češi :)
P.S ako sam nešto lupio, ne zamerite, jer sam računao dok sam pisao... [ hiho @ 03.03.2006. 12:07 ] @
A sta mislite o ovome (osim sto ima greskica na engleskom) http://www.bertrands-paradox.com ??????!!!!!!!!!!! [ hiho @ 03.03.2006. 12:09 ] @
zar ne mislite da je to resenje paradoxa?
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|