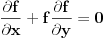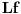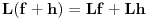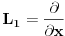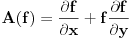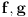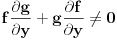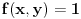[ R A V E N @ 22.05.2010. 19:06 ] @
|
[ Nedeljko @ 23.05.2010. 05:18 ] @
[ R A V E N @ 24.05.2010. 17:16 ] @
U redu... a šta je sa mojim pristupom? Ja sam to probao na isti način kako je izloženo u knjizi Walter A. Strauss - Partial Differential Equations, An Introduction:
 Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|