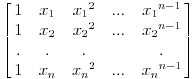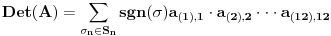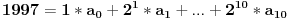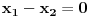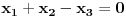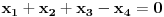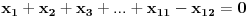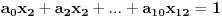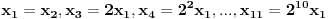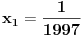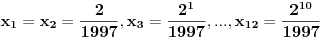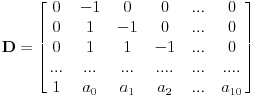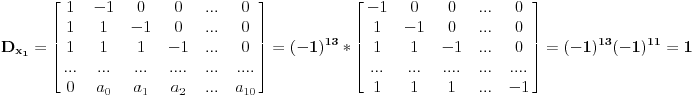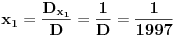Da li si ikako probao da rešiš zadatak? Znaš li osnovne teoreme u vezi sa determinantama? Znaš li npr. Vandermondovu determinantu, Lagranžovu teoremu?

Van-der-Mond-ova matrica bi trebala biti oblika


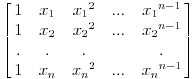
ako se ne varam... e sad, ovo mi ne upucuje (barem ne meni) na rjesenje, jer rezultat te matrice jeste proizvod, a max sto mogu dobiti od svakog faktora proizvoda je 2,a 1997 nije stepen dvojke...

ono sto sam ja prvobitno kontao jeste, da kada se razvije matrica, dobijemo sume nekih pozitivnih i negativnih brojeva... odredjena kombinacija bi dala broj 1997... odnosno, kad predstavim recimo a kao zbir svih pozitivnih, a b kao zbir svih negativnih, onda imam oblik a-b=1997.. sad bi bio fazon naci neki nacin kako dokuciti sta su a i b...

Lagrange... sjecam se da je spominjan na predavanjima, ali ne mogu da se sjetim u kom kontekstu i kada...

Ima Niko se ne javlja jer izgleda da zadatak nije lak.Ja bih počeo ovako:
Napišem determinantu sa dvanaest jedinica dijagonalno (odozgo lijevo do dole desno) i sve ostalo unutra neka su nule.Ova determinanta 12-tog reda ima vrijednost 1 što i nije loše za početak.U donjem desnom uglu formiram D drugog reda tako što umjesto dvije nule stavim 1i-1.Ova mala D2 ima vrijednost 2,ali i
D12 ima tu vrijednost.Sad idemo na pravljenje D3 tako da ona ima vrijednost D3=D2+D2=4.(Nule promjeniti samo tamo gdje se mora.)Tjerajmo ovu rekurziju dalje D4=D3+D3=8 itd sve dok ne ispane D12=2048.Nije loše al je previše.Treba nam 1997 tj za 51 manje.

Zadatak radim ovako napamet pa neko treba to lijepo okončati.
Čini mi se da je do sada pored dijagonale nestalo svih nula na lijevoj strani osim 11 u prvoj koloni,a desno od dijagonale nestalo je samo 11 nula u zadnjoj koloni.Ove nule daju šansu da se nešto izmjeni i odbije onih -51.

Nasao sam da je maksimalni moguci broj koji se dobije za matricu 12x12 ravno 2 985 984 (Hadamard maximal determinant problem) ... a ta metoda sa rekurzijom "izgleda" bi trebala dati trazeni odgovor... idem isprobavati...

_{[Ovu poruku je menjao NTManiac dana 30.05.2010. u 22:18 GMT+1]}

Može se napraviti neparna vrijednost, naprimjer ovako



Pa polako tjerati rekurzivno da svaka veća bude neparna.Ovu neparnu možemo vući po dijagonali a dodavati na nju parne vrijednosti 1 ili više u svakom koraku.Samo treba to lijepo dokazati a ne na silu.

Naprimjer za D3=3
D4=3+4=7
D5=7+8+8=23
D6=23+16 +8=47
i tako nekako dalje pa bi ispalo da je 1997=3+mnogo parnih.
S tim da se jasno vidi da su ove parne moguće na datom nivou.

Trenutno nemam vremena da rješavam zadatak, ideja je sledeća:

riješiti zadatak primjenom definicije determinanti preko permutacija; pošto su svi elementi -1, 0, 1 svaki član u sumi je jednak -1, 1 ili 0 jer je proizvod elemenata determinante; pitanje je moze li kompletna suma (tj. sama determinanta) da bude 1997? 1997 je neparan broj; mozda ima veze sa parnim, neparnim permutacijama?

Nemam vremena, spremam Verovatnoću.

Svaki član u sumi je 1, -1 ili 0.

Da bi vrijedilo Det(A)=1997, mora da bude:

x članova u gornjoj sumi koji su jednaki -1;
x+1997 članova u gornjoj sumi da su jednaki 1;
12!-(2x+1997) članova koji su jednaki nuli (neparan broj nula).

Pokušavao sam dalje da riješim zadatak pomoću kombinatorike ali ne ide. Krenuo sam od toga da mora biti neparan broj nula...

Malo bih zauzet ispitima, ali evo konacno se rijesi:

Fazon je gledati 1997 u binarnom obliku, kao:



Sada neka imamo ovakav sistem:




...



U ovoj jednacini je

Ovo ubacimo u zadnju jednacinu pa je:

Odakle je:

Pa je:


Ova znaci da jednacina ima jedinstveno rjesenje kada je vrijednost determinante razlicita od nule. Pa imamo:



Onda je:




Odnosno:

sto znaci da je D=1997... Time je pokazano da postoji trazena determinanta...

Kako je 1997 u binarnom sistemu 10110011111 onda je: