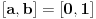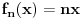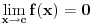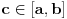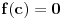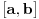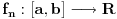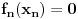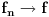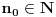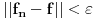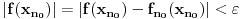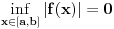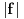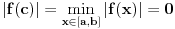[ number22 @ 29.05.2010. 20:27 ] @
|
| U prostoru neprekidnih funkcija na segmentu C[a,b] dat je skup A koji sadrzi sve (neprekidne) funkcije koje imaju bar jednu nulu na [a,b]. Dokazati da je skup A zatvoren skup u C[a,b].
Pokusao sam da dokazem da A sadrzi granicnu funkciju svakog konvergentnog funkcionalnog niza iz A, jer bi to znacilo da je skup zatvoren. Ali ne ide mi nesto. Dobijem da granicna funkcija tezi nuli u nekoj tacki segmenta sto ne mora znaciti da je element skupa A. Mozda ovo i nije najlaksi nacin za dokaz... |
[ Nedeljko @ 29.05.2010. 22:02 ] @
Neka je
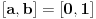
i
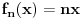
. Ovo je niz neprekidnih funkcija koje u datom segmentu imaju nulu, ali taj niz funkcija divergira. Navedeni skup nije zatvoren.
[ number22 @ 30.05.2010. 00:34 ] @
Nisu ni bitni divergentni nizovi, samo konvergentni.
Evo kako sam ja pokusao.
Neka je fn konvergentan niz funkcija iz A koji konvergira ka f. Tada niz i ravnomjerno konv. ka f. Pa za svako €>0 (epsilon) i dovoljno veliko n (vece od n0) imamo
| fn(x) - f(x) | < € za svako x iz intervala. Neka je k > n0 i neka funkcija fk(x) ima nulu u tacki c intervala [a,b]. Pa je
| fk(c) - f(c) | < €, a odavde je
| f(c) | < €, sto znaci da je
lim f(x) = 0 (kad x tezi c). E sta sad? Jel ovo znaci da f ima nulu u [a,b]?
[ Nedeljko @ 30.05.2010. 10:01 ] @
E, da, ja sam dokazao da taj skup nije kompaktan.
Da, ako je

neprekidno i
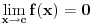
i
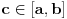
(što je ispunjeno zbog zatvorenosti domena), onda je
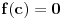
.
[ number22 @ 30.05.2010. 11:31 ] @
f je neprekidno zbog ravnomjerne konvergencije (posto su i fn neprekidne).
Znaci, vazi da je f(c) = 0, zato sto je c iz segmenta [a,b] i f je neprekidno. A da je (a,b) npr. interval ne bi moralo to da vazi? Pa je i skup A zatvoren.
[ Nedeljko @ 30.05.2010. 12:10 ] @
Da.
[ number22 @ 12.06.2010. 20:32 ] @
Opet je netacno. A obrazlozenje je da iz |f(c)|<€ (za svako €<0) ne slijedi da je
lim f(x) = 0 (kad x tezi c) bez obzira sto je c iz segmenta[a,b]...
[ atomant @ 12.06.2010. 21:01 ] @
Vajerstrasova teorema vam resava ovo. Ona tvrdi da, ako je

neprekidna na zatvorenom intervalu
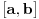
onda je ona i ogranicena na
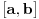
. Ne secam se dokaza.
[ Nedeljko @ 12.06.2010. 21:43 ] @
Evo kompletnog rešenja:
Neka
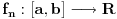
neprekidno i neka je
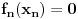
. Pretpostavimo da
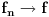
ravnomerno na
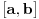
. Jasno, u tom slučaju

mora biti neprekidno.
Neka je

. Izaberimo takvo
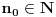
da za svako

važi
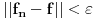
. Tada je
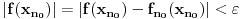
, pa je
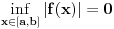
. Međutim, zajedno sa

i funkcija
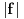
mora biti neprekidna, pa dostiže minimum u nekoj tački
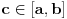
, pa je
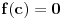
.
[ number22 @ 13.06.2010. 10:27 ] @
Da li onda moze biti
c=a (ili b) i f(c) razlicito od nula iako je |f| neprekidno?
[ Nedeljko @ 13.06.2010. 11:32 ] @
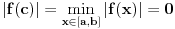
.
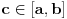
.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.