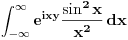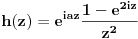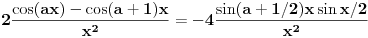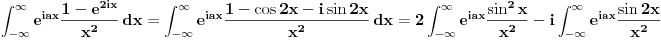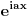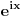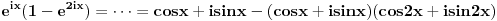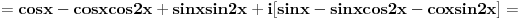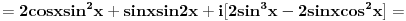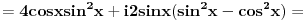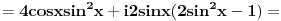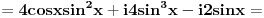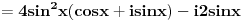[ Dinaaaa @ 02.06.2010. 15:27 ] @
|
[ Mlatko @ 03.06.2010. 14:02 ] @
Garant si se obradovala kad si vidjela da ti je neko odgovorio, ali nazalost slijedi razocaranje :)
Naime, prije nego krenemo u rjesavanje moram pitati - je li tebi problem bas konkretno ovaj integral ili opcenito nemas ideju kako rjesavati integrale na taj nacin? Jer prema tonu tvog posta cini mi se da se radi o ovom zadnjem, a u tom slucaj bi sigurno bilo svrsishodnije prouciti metodu na nekim jednostavnijim primjerima, odnosno uputiti te na dijelove iz literature u kojima se obradjuje ta metoda, pa se onda vratiti rjesavanju ovog zadatka. Ukoliko je pak problem bas ovaj integral, onda naravno ima smisla, pa eto ocekujem tvoj odgovor uz isprike ako sam pogresno procijenio tvoje pitanje. [ Dinaaaa @ 03.06.2010. 15:55 ] @
Do skoro nisam imala pojma kako resavati integrale na taj nacin, ali sam se bacila u istrazivanje. Skontala sam nacin resavanja na primerima tipa
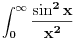 , , 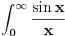 i jos nekim primerima sa eksponencijalnim funkcijama. Odredim singularitete f-je h, nadjem odgovarajucu zatvorenu konturu i krivolinijski integral po njoj je 0. Integral po konturi se sastoji od nekoliko integrala po pojedinim njenim delovima. Neki od tih delova kad se saberu treba da daju ovaj integral koji se trazi. Od nule oduzeti integral po ostatku konture (racuna se primenom racuna ostataka) i rezultat je trazeni integral. Znaci imam konkretno problem sa ovim integralom, sto je verovatno posledica neuvezbanosti. Ili biram pogresnu konturu, ili pravim gresku prilikom racuna, ili je nesto trece :)). Svakako ima smisla raditi ovde ovaj integral, bice mi od velike koristi jer mi treba za Furijeovu transformaciju i jos nekim primerima sa eksponencijalnim funkcijama. Odredim singularitete f-je h, nadjem odgovarajucu zatvorenu konturu i krivolinijski integral po njoj je 0. Integral po konturi se sastoji od nekoliko integrala po pojedinim njenim delovima. Neki od tih delova kad se saberu treba da daju ovaj integral koji se trazi. Od nule oduzeti integral po ostatku konture (racuna se primenom racuna ostataka) i rezultat je trazeni integral. Znaci imam konkretno problem sa ovim integralom, sto je verovatno posledica neuvezbanosti. Ili biram pogresnu konturu, ili pravim gresku prilikom racuna, ili je nesto trece :)). Svakako ima smisla raditi ovde ovaj integral, bice mi od velike koristi jer mi treba za Furijeovu transformaciju  faktora. faktora.[ petarm @ 03.06.2010. 18:13 ] @
Napisi neki svoj postupak. Dokle si stigla i gde je zapelo!
[ Dinaaaa @ 03.06.2010. 21:33 ] @
Petarm, sto me mucis :).
Atasovala sam fajl u kome sam nacrtala kako izgleda kontura. Podebljanom linijom je oznacena kontura po kojoj racunam integral. 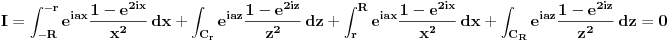 Integracija po 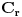 je u smeru kretanja kazaljke na satu, a po je u smeru kretanja kazaljke na satu, a po 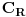 u suprotnom smeru od smera kretanja kazaljke na satu. u suprotnom smeru od smera kretanja kazaljke na satu.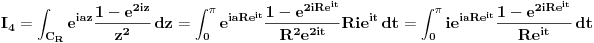 jer je na jer je na 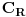 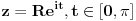 Dalje imamo da vazi: 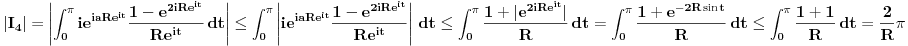 Koristi se da je 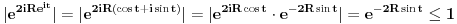 jer je jer je 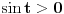 i R>0. i R>0.Sad imamo da je 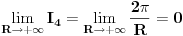 Sad treba sabratai integrale 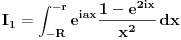 i i 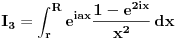 tako da se u njihovom zbiru pojavi tako da se u njihovom zbiru pojavi 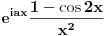 jer je jer je 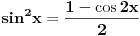 . Ja uvedem smenu kod . Ja uvedem smenu kod 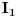 i dobijem integral sa granicama kao i i dobijem integral sa granicama kao i 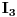 , koristim i da je , koristim i da je 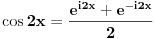 . Ali kad saberem . Ali kad saberem 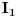 i i 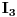 ne mogu da dobijem pogodan izraz. ne mogu da dobijem pogodan izraz.I naravno, treba jos izracunati 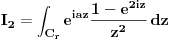 . To cu kucati kad mi protumacite ovaj deo sto sam kucala. Mislim da je prvi deo u redu jer sam radila kao u jednom slicnom primeru koji imamm uradjen i to mi je jasno. Problem je ovaj deo oko sabiranja integrala. . To cu kucati kad mi protumacite ovaj deo sto sam kucala. Mislim da je prvi deo u redu jer sam radila kao u jednom slicnom primeru koji imamm uradjen i to mi je jasno. Problem je ovaj deo oko sabiranja integrala.[ Mlatko @ 06.06.2010. 04:35 ] @
Citat: Dinaaaa: Problem je ovaj deo oko sabiranja integrala. Ne trebas sabirati te integrale (afaik to bi radila da su ti granice zadanog integrala od 0 do +beskonacno, pa ti treba sabiranje da bi zakljucila o eventualnoj parnosti podintegralne funkcije, te konacni rezultat (ovog sa beskonacnim granicama) samo podijelila sa dva.) U tvom slucaju (rekla si da je ovo Furierov transform) dovoljno ti je znati *glavnu vrijednost* zadanog integrala. A ta glavna vrijednost zadanog integrala ce postojati ako postoji limes (kad R->besk i r->0) zbroja integrala I1 i I3. Ti si pokazala da je u slucaju kad R->besk I4=0. Jos trebas samo izracunati koliki je I2, odnosno njegov limes kad r->0. Ne znam na koji nacin si ga izracunala, ali najjednostavnije je preko tvrdnje: 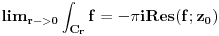 koja vrijedi za analiticke funkcije u okolisu pola z0 (nas pol je 0), gdje sam odmah uracunao da kruzni luk C_r ide u negativnom smjeru od pi do 0. Nakon sto izracunas reziduum u nuli (jednak je -2i), dobije se da je taj limes jednak 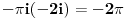 . .Dakle 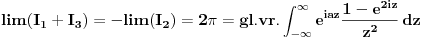 . .Sad jos samo preostaje ovu kompleksnu verziju integrala transformirati u oblik iz kojeg cemo iscitati rjesenje naseg pocetnog integrala. Pri tome uzimamo naravno da je z realno na intervalu integracije, pa trebamo modificirati 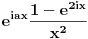 tako da u konacnom izrazu dobijemo  Nakon nekoliko redova trigonometrije (koje sam omaskom pojednostavnio racunajuci da je a=1, a sad mi se ne da ponovo a i bojim se da se da ce se zakomplicirati :) ) dobije se:  Ovaj zadnji integral je jednak nuli, i dobijemo konacno rjesenje zadanog integrala uz a=1:  . . Vjerojatno bi trebalo nesto i diskutirati za  u opcem slucaju. u opcem slucaju.p.s Sve ovo uzmi ipak s rezervom jer sam kompleksnu davno imao a zanimljivo ovaj dio materije uopce nismo obradjivali. [ Dinaaaa @ 19.06.2010. 20:20 ] @
[ Mlatko @ 22.06.2010. 00:25 ] @
[ Dinaaaa @ 22.06.2010. 15:30 ] @
Ok, u sustini radili smo isto, razlika je sto kad se ubaci ovo a, stvari se komplikuju :))). Primenjujuci tvoj postupak, ne stavljajuci da je a=1, dobija se:
 Ja se vodim glavnim problemom :))). Od muke, moram ga navesti ovde :))). - Dokazati da je Furijeova transformacija f-je (teta-faktor): 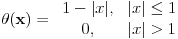 f-ja 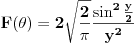 . .Taj deo dokazem i to mi je sigurica da je zadatak ispravan. Treba sad dokazati inverznu transformaciju, a znamo da je 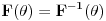 . Znaci resavanjem onog integrala sa pocetka treba da se dobije rezultat u kome se pojavljuje |a|, tj. nesto oblika . Znaci resavanjem onog integrala sa pocetka treba da se dobije rezultat u kome se pojavljuje |a|, tj. nesto oblika 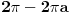 i i 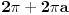 , u zavisnosti od a. Ja ne vidim drugi izlaz osim resavanja , u zavisnosti od a. Ja ne vidim drugi izlaz osim resavanja 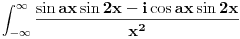 . Drugi integral uz i je 0. Da li je moguce na "pristojan nacin" :))) resiti ovaj prvi, kao parametarski integral ili na neki drugi nacin? . Drugi integral uz i je 0. Da li je moguce na "pristojan nacin" :))) resiti ovaj prvi, kao parametarski integral ili na neki drugi nacin?Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|