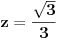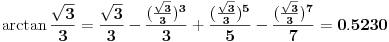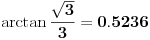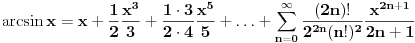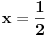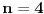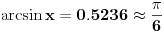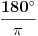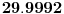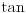Hm, koja skola je to u pitanju? Jedino sto mi pada na pamet je preko Maklorenovog reda, a to se sigurno ne uci u srednjoj nego na fakultetu. Postoje jos neki nacini, pa sta ti odgovara

1. preko Maklorenovog reda




E sad, drugo pitanje je sta je Maklorenov red i kako se do njega stize.



2. ili na drugi nacin (kompleksna analiza)






3. postoji i Ojlerov razvoj funkcije arctg u red

Pa i u 3. slucaju koliko je n jel je nula.

Ako npr. trazimo arctg od sqr(3)/3, odnosno korena iz 3 sa 3.
Koji broj uzimamo za n.




_{[Ovu poruku je menjao Maksa12 dana 09.06.2010. u 22:32 GMT+1]}

sve ili dovoljno mnogo. od 0 do beskonacno. to je aproksimacija beskonacnim redom. sto vise uzmes n-ova to je tacniji rezultat. sve su ovo aproksimacije beskonacnim redovima (cak i ovo drugo, iako nije red, moze da uzima vrednost do beskonacno).

ako uzmes maklorenov red (ovo pod 1) i kazes





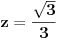
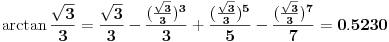
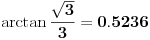
Ako koristis digitron, dobices da je . Znaci, razlikuju se tek na 4. decimali. Ako uzmes jos clanova reda, razlika ce biti jos manja. Isto vazi i za ostale redove. Ovo je mozda najbolje za pocetak. Ojlerov red je malo tezi i za shvatanje i za racunanje. Npr. za n od 0 do 5, Ojlerov red daje istu vrednost kao i digitron na tih recimo 4 decimale. Za n od 0 do 20, razlikuju se tek na 13. decimali dok se za isto n (od 0 do 20) kod Maklorenovog reda razlikuju na 12. decimali. Dakle, Ojlerov je tacniji za vece n, ali to je nebitno. Koristi prvi, sa prvih par clanova i dosta je. Dosta je i sa 4 i to je dovoljno tacno za skolsku primenu :)

Akako se vadi faktorijel razlomka i decimalnih brojeva?

Ako npr. 5!=5*4*3*2*1 , kako se onda trazi (3/5)!

?

faktorijel je definisan za prirodne brojeve. znaci n mora biti prirodan! mada sam negdje na forumu vidio, cini mi se, da preko neke aproksimacije traze i faktorijel bilo kojeg pozitivnog realnog broja...

Da, samo što to nije faktorijel, već analitičko produženje. Najtačniji odgovor je dao Kolins Balaban da je faktorijel definisan samo na celim nenegativnim brojevima, jer ima beskonačno načina da se faktorijel produži (čak i analitički uz očuvanje svojstva f(n)=nf(n-1)). No, ovo je za postavljača pitanja svakako korisna informacija.

Vidi npr.

http://citeseerx.ist.psu.edu/v...3557&rep=rep1&type=pdf

A ako imamo jednacinu sinx=1/2, moze li se do toga da je x=30 doci nekako "rucno"? pomocu neke formule, funkcije, ili crteza,...?

Zašto je x=30? Šta je 30? Šta je sin?

Mislim da nije bilo odgovora na pitanje koja je to škola u pitanju, pošto od toga dosta zavisi kakav odgovor želiš. Ne razumem i ono "za neko X" u pitanju, da li imaš neku konkretnu vrednost (kao ovde 1/2) ili ti treba postupak za bilo koje X?

Mislim na to kako "rucno" naci:
sin od koliko stepeni je 1/2 ?

Najprostije je da koristis Maklorenov red za aproksimaciju funkcije arcsin.

gde je


Ako ides do dobices da je

I sada, ako to zelis da pretvoris u stepene, moras da pomnozis sa . Dobices

Naravno, za ove neke karakteristične vrednosti možeš i geometrijski da odrediš. Mislim da je to bliži odgovor tvom nivou školovanja. Korišćenjem adicionih formula, formula za polu ugao i slično možeš da proširiš broj karakterističnih vrednosti za koje možeš da rešiš jednostavnu trigonometrijsku jednačinu tog oblika.

Korišćenje Maklorenovog reda je grubo rečeno ono kako to digitron radi, i omogućava ti da izračunaš vrednost za bilo koje x, ali je rezultat samo aproksimacija (teži rešenju što više članova dodaješ).

moze li se taj arctg nekako izvesti pomocu sestara,lenjira, uglomera,..., kada nacrtamo trigonometrijski krug?

Arcus = luk.

Arcus tangens = luk (isto što i ugao) „tangensa“.

Drugim rečima, ugao (arcus tangens) je argument funkcije .

Ako ti je jasno šta je na trigonometrijskom krugu tangens, onda je arkus tangens ugao tog tangensa.