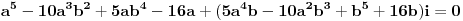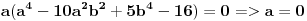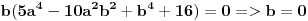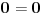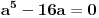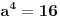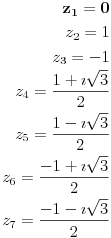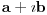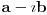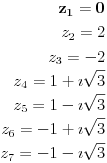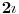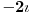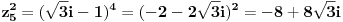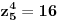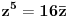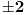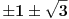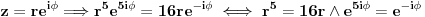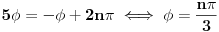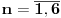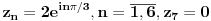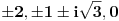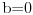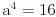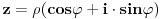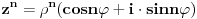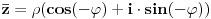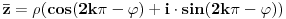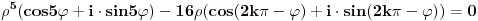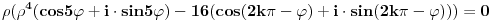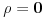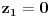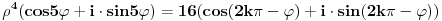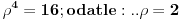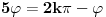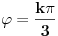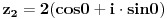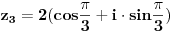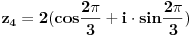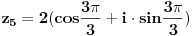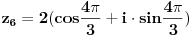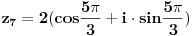[ sava999 @ 11.06.2010. 11:23 ] @
| Pozdrav, imam problema sa rijesavanjem jednog zadatka, bio bih zahvalan ako bi mi neko mogao objasniti kako se rijesavaju zadatci ovakvog tipa. Nisam mogao naci na forumu slican zadatak, ako postoji brisite temu i posaljite mi pp :) Znaci rijesti jednacinu: z^5 = 16z gdje je z, z kompleksno. Hvala |