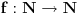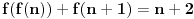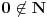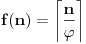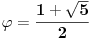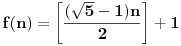Ovo je verovatno zadatak sa republickog ili saveznog ili mozda cak i neke olimpijade. Sumnjam da ce ti neko resiti to na ES-u.

Hajmo, ovako:

f(f(1))+f(2)=3

Odatle je f(2)<=2

Ako bi bilo f(2)=1, onda bi bilo f(f(1))=2, kao i f(f(2))+f(3)=4, odnosno f(1)+f(3)=4, odakle je f(1)<=3. Zbog f(f(1))=2 ne može biti niti f(1)=1, niti f(1)=2, pa mora biti

f(1)=3, f(2)=1, f(3)=2.

Međutim, onda se jednakost f(f(2))+f(3)=4 svodi na 5=4. Ovo je kontradikcija sa pretpostavkom f(2)=1, pa mora biti

f(2)=2, f(f(1))=1.

Ako za svako 2<=k<=n sledi 2<=f(k)<=k, onda zbog f(n+1)=n+2-f(f(n)) važi i 2<=f(n+1)<=n, pa je sa

f(2)=2, f(n)=n+1-f(f(n-1)) za n>=3,

funkcija jednoznačno određena za n>=2.

U tom slučaju je f(f(1))=1 moguće samo za f(1)=1. Dakle, postoji tačno jedna takva funkcija i određena je rekurentnom relacijom

f(1)=1,
f(n+1)=n+2-f(f(n)).

Kakvo potcenjivanje.

Možda će nekom biti zanimljiva i eksplicitna formula: , gde je .

Ili u ekvivalentnom obliku,

Još da neko dokaže da ta funkcija zadovoljava jednačinu.