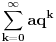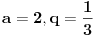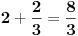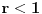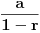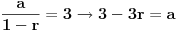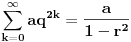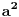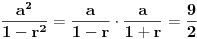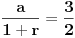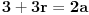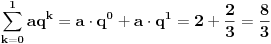[ Maksa12 @ 14.06.2010. 21:59 ] @
| Zbir beskonacne geometrijske progresije je 3, a zbir kvadrata svih njenih clanova je 9/2. Koliki je zbir prva dva clana progresije? Kako se radi ovaj zadatak? Ja treba da polazem prijemni, sve zadatke sam resio, ali ovaj nemam pojma. Isao sam na pripreme dobio sam probni test prijemnog, i dobio sam taj zadatak. U testu pise samo zadatak i da je resenje 8/3, ali do tog resenja treba nekako doci. Zna li neko kako se on radi? Hvala! [Ovu poruku je menjao Maksa12 dana 14.06.2010. u 23:14 GMT+1] |