[ Zer0ha @ 15.06.2010. 06:14 ] @
| Odrediti zapreminu figure ograničene krivom Z= (y-2x)e^2y i ravnima z=0, y=-2x ,y=1-2x,y=2x i y=2x-1 zna li ko ? |
|
[ Zer0ha @ 15.06.2010. 06:14 ] @
[ zzzz @ 15.06.2010. 08:39 ] @
Šta ne znaš,riješiti integral ili odrediti granice integracije?
[ Zer0ha @ 15.06.2010. 11:06 ] @
Granice i sliku , i resenje po mogucstvu :D
[ zzzz @ 15.06.2010. 11:59 ] @
Ajde kad kažeš.Evo granica!A sad ti nastavi bar malo.Odredi
predznak funkcije Z= (y-2x)e^2y nad onom žutom plohom ograničenom pravcima. 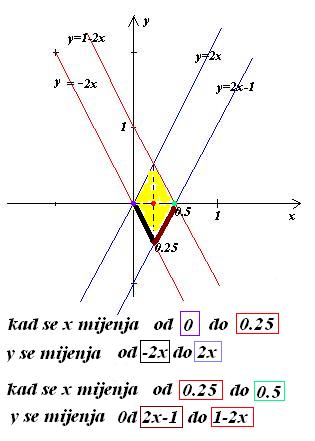 [ Nedeljko @ 15.06.2010. 16:45 ] @
Očigledno je -1<y-2x<0.
[ Zer0ha @ 15.06.2010. 17:44 ] @
Znaci POLUDECU a jel mozes da mi uradis zadatak do kraja da ne pises 0.5 nego da ostavis u razlomku ili kako vec
[ zzzz @ 15.06.2010. 19:18 ] @
[ Zer0ha @ 16.06.2010. 09:17 ] @
A koja se ovde zapremina racuna ne razumem kako ti znas da su granice 1/4 i 0 i 2x i -2x to me buni integral nije problem njega znam
[ Nedeljko @ 16.06.2010. 09:59 ] @
[ atomant @ 16.06.2010. 10:25 ] @
Vide se granice sa slike. x ide od 0 do 1 a y od -0.5 do 1. Nacrtao sam samo
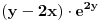 i i  jer kada bih nacrtao i dodatne 4 ne bi se videlo koja je zapremina u pitanju. Ostatak ces morati da "zamislis" jer kada bih nacrtao i dodatne 4 ne bi se videlo koja je zapremina u pitanju. Ostatak ces morati da "zamislis"    Vidis da je tvoja figura ispod z=0. Odozdo je ogranicena ovom funkcijom, odozgo sa z=0 a sa strane ostalim funkcijama. Dobijas nesto sto lici na prizmu sa romboidnom osnovom, samo sto je donji kraj u obliku ove funkcije [ zzzz @ 16.06.2010. 12:57 ] @
Citat: Zer0ha: A koja se ovde zapremina racuna ne razumem kako ti znas da su granice 1/4 i 0 i 2x i -2x to me buni integral nije problem njega znam Ja sam nacrtao pogled iz ptičje perspektive na ravan z=o. U zadatku su date četiri ravni koje su okomite na xu ravan (z=0) Ja sam nacrtao prodore tih ravni kroz z=0 ravan i to su ona četiri pravca koja okružuju žuto obojenu plohu.To je onaj romb kome znam koordinate vrhova.Ako pomjeramo ovaj romb duž z ose to bi ličilo na neku prizmu. Odsječemo tu prizmu ravninom z=0 sa jedne strane,a sa druge zadanom prostornom zakrivljenom plohom Z= (y-2x)e^2y. Nedeljko je provjerio da li se ove dvije plohe sijeku unutar romba i našao da to nije slučaj.Da se to desilo imali bi dio zapremine ispod xy (-) ravni a dio iznad (+) pa bi morali o tom voditi računa. Kako izračunati ovako omeđenu zapreminu? Izračunam diferencijalno mali dio dxdy(Z2-Z1)=dxdy((y-2x)e^2y-0) u opštem obliku. Sad pomoću ovoga računam zapreminu diferencijalno tanke šnite,debljine dx, između dviju ravni y=-2x i y=2x.To napišem matematički: 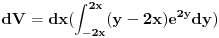 Kad riješim ovaj integral imam zapreminu diferencijalno tanke šnite u opštem obliku (u funkciji od x),ali samo do polovice romba.Od pola pa dalje granice su drukčije. Konačno računanje zapremine na lijevoj polovici romba je integracija ovih diferencijala od x=0 do x=1/4.  Ubacivanjem izračunate opšte vrijednosti za Dv,integracijom i konačno uvrštenjem granica za x dobijemo prvi dio zapremine.Drugi dio računamo istim postupkom. --------------- Mogao sam i nešto drukčije usvojiti granice i promjeniti redoslijed integracije.Ako bih uzeo da mi diferencijalne šnite leže paralelno sa x osi umjesto y,onda bi imao: Dok se y mijenja od -1/2 do 0 , x se mijenja od -y/2 do (y+1)/2, a dok se mijenja od ?? do ?? , x se mijenja 0d ?? do ?? (da li bi znao naći ove 4 granice?Ako znaš imaš pravo postavljati još pitanja. [ Zer0ha @ 16.06.2010. 18:09 ] @
Hvala vam ljudi SKONTO SAM
Dok se y menja 0 do 1/2 , x se menja od y/2 do (1-y)/2 jel tako a ovaj zadatak z=sin(koren(x^2+y^2)) ogranicen cilindrom x^2 + y^2 = Pi^2/4 i ravni z=0 samo granice kako postavljam kod dvojno malo me to buni [Ovu poruku je menjao Zer0ha dana 16.06.2010. u 19:43 GMT+1] Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|