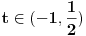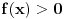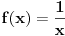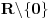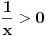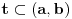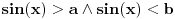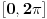[ Nikola 23 @ 15.06.2010. 21:52 ] @
| sinx<cos2x na segmentu [0,2*pi] ja sam poceo da ga radim: sinx<cos^2 x-sin^2 x zna se da je sin^2 x+cos^2 x=1 pa je onda cos^2 x=1-sin^2 x sinx<1-sin^2 x-sin^2 x sinx<1-2*sin^2 x prenesemo sin x na desnu stranu 1-2*sin^2 x-sinx>0 -2*sin^2 x-sinx+1>0 smena t=sinx -2t^2-t+1=0 izracunamo kvadratnu jednacinu ... t=1 ili t=1/2 , tako da je sinx=1 ili sinx=1/2, onda je x=pi/2+2*k*pi ili x=pi/6+2*k*p. znamo resenje, kako sada da odredimo oblast definisanosti funkcije U resenju pise da je oblast definisanosti funkcije [0,pi/6)U(5*pi/6,3*pi/2)U(3*pi/2,2*pi] , ali kako doci do tog resenja. |