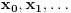
Nadji prvi izvod i izjednaci ga sa nulom. Nadji drugi izvod i ubaci vrednosti koje si dobio iz jednacine . Ako opet dobijes nulu nadji treci izvod i tako dok ne dobijes vrednost razlicitu od 0. U tom slucaju, ako je red tog izvoda paran, funkcija ima lokalni ekstremum i to

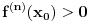
1.) lokalni minimum ako je odnosno
2.) lokalni maksimum ako je .

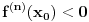
U slucaju da je red izvoda neparan, funkcija ima prevojnu tacku.


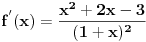
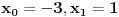
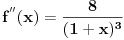
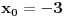
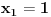
U ovom tvom slucaju, prvi izvod funkcije je . Odatle sledi su kandidati za ekstremum . Kada nadjes drugi izvod ( ) dobices da je on u obe ove tacke razlicit od 0, tj. tacka je lokalni maksimum, a tacka lokalni minumum funkcije.

Gdje se moze naci dokaz ove teoreme ? Zar nije dovoljno ispitati znak drugog izvoda u okolini tacke kandidata.

A sta ako je drugi izvod jednak nuli u okolini te tacke? Proveri, jeste. Inace, da upotpunim sa grafikom:






Ne znam dokaz, davno je to bilo na faxu (pre 3 godine :) )

Pa, onda je funkcija linearna u okolini te tačke.

Dokaz ide indukcijom po. Ako je i je neprekidno u nekoj okolini tačke , onda je rastuće u okolini tačke , pa zbog funkcija opada do , a raste posle toga, pa u tački ima minimum (jednak nuli), pa je nenegativna u okolini tačke i onda se primenjuje induktivna pretpostavka.