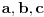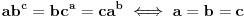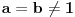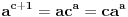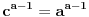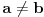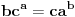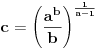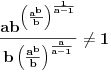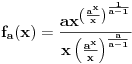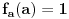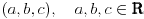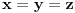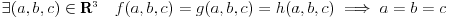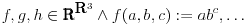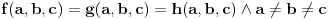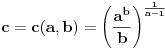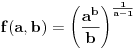[ Farenhajt @ 17.06.2010. 13:14 ] @
|
[ Bojan Basic @ 17.06.2010. 18:33 ] @
[ holononi @ 17.06.2010. 18:58 ] @
Ja ću da rešim ovaj (<=) smer:
a=b=c => abc = abc = abc [ Farenhajt @ 17.06.2010. 20:31 ] @
Citat: Bojan Basic: Samo da proverim — prema prednosti operacija, pretpostavku čitamo kao 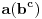 itd.? itd.?Upravo tako. Varijanta 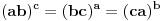 "odokativno" deluje kao nešto lakša, ali može i ona da se uradi za zagrevanje. "odokativno" deluje kao nešto lakša, ali može i ona da se uradi za zagrevanje.Citat: Zadivljujuće! [ holononi @ 17.06.2010. 22:16 ] @
Dobro malo sam se našalio. Ali u čemu je kvaka kod ovog zadatka? Za njegovo rešavanje nije potrebna nikakva teorija. Šta spremaš prijemni?
[ Farenhajt @ 18.06.2010. 10:07 ] @
Pa ok, ako je trivijalan, prezentiraj nam svoje rešenje u dva reda.
[ Nedeljko @ 18.06.2010. 11:11 ] @
[ holononi @ 20.06.2010. 22:24 ] @
Ako se podje od tačke (a, b, c) = (1, 1, 1) koja je rešenje i posmatra priraštaj promenljivih tada
a1 = a + h, h > 0 proizvoljno malo Tada abc raste linearno bca raste eksponencijalno cab raste kao stepena funkcija. Da bi važila jednakost ove priraštaje treba kompenzovati i to tako da svaki član ima isti priraštaj. Zato b1 = b + h, c1 = c + h, odnosno a1 = b1 = c1. Isto i za h < 0 samo što tada članovi opadaju. Kako su svi članovi po uslovu zadatka neprekidne funkcije nema drugih rešenja. [ Nedeljko @ 21.06.2010. 00:09 ] @
Ala ti je argument!
Citat: holononi: Zato b1 = b + h, c1 = c + h, odnosno a1 = b1 = c1. Odakle ti jednakost priraštaja promenljivih? [ holononi @ 21.06.2010. 05:50 ] @
Samo jednakost priraštaja svih promenljivih održava jednakost svih članova.
[ Nedeljko @ 21.06.2010. 09:12 ] @
Dokaži.
[ holononi @ 21.06.2010. 12:46 ] @
Ako ti koristiš monotonost koju nisi dokazao zašto ja moram da dokazujem?
[ Nedeljko @ 21.06.2010. 13:18 ] @
Ja sam lepo napisao da ostaje da se dokaže monotonost. Bez toga rešenje nije kompletno, kao ni tvoje.
[ holononi @ 21.06.2010. 13:37 ] @
A šta treba dokazati u mom rešenju?
[ Nedeljko @ 21.06.2010. 14:17 ] @
Pa, to što tvrdiš
Citat: holononi: Samo jednakost priraštaja svih promenljivih održava jednakost svih članova. [ Cabo @ 21.06.2010. 15:12 ] @
@holononi:
Priraštaji nisu jednaki u opštem slučaju. Ponovi Analizu 2, funkcije više promenljivih. [ holononi @ 21.06.2010. 16:48 ] @
Ako priraštaji nisu jednaki tada postoji tačka (a, b, c), a <> b <> c <> a koja zadovoljava uslove zadatka. Ne budi ti teško pa nam navedi tu tačku.
[ Cabo @ 21.06.2010. 17:06 ] @
[ holononi @ 21.06.2010. 17:11 ] @
Ja se prep'o, zavlačim se pod ormar da promadjem sve knjige i sveske iz analize 2 a ti ni zadatak nisi pročitao.
[ Cabo @ 21.06.2010. 17:12 ] @
[ holononi @ 21.06.2010. 17:23 ] @
Pa dokaži tu negaciju. Uzgred, pogledaj koji je domen pa će ti možda biti jasnije.
[ Cabo @ 21.06.2010. 17:26 ] @
Rado, ali trenutno nemam vremena.
[ Bojan Basic @ 21.06.2010. 17:46 ] @
Holononi, ti, izgleda, ne znaš značenje pojma dokaz. To što Cabo eventualno ne može da nađe tačku za koju tvoj argument pada i dalje ne znači da ti je argument matematički ispravan. Evo ilustracije.
Problem: Ispitati da li za 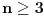 u skupu u skupu 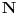 postoji rešenje jednačine postoji rešenje jednačine 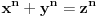 . .Moje „rešenje“: Data jednačina ekvivalentna je sa 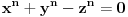 . Kada je zapišemo u ovom obliku, odmah vidimo da nema rešenja. . Kada je zapišemo u ovom obliku, odmah vidimo da nema rešenja.Cabo prigovara: Čekaj, ne slažem se da se iz tvog oblika odmah vidi da jednačina nema rešenja. Dokaži i taj deo. Ja odgovaram: Ako jednačina u mom obliku ima rešenje, tada postoji tačka 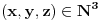 za koju je ispunjeno za koju je ispunjeno 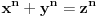 . Ne bilo ti teško, navedi tu tačku. . Ne bilo ti teško, navedi tu tačku.Da li sad vidiš koliko ti je argumentacija šuplja? Matematika se ni u ludilu tako ne radi. Ali OK, ako bi i dalje terao po svome, evo konačnog udarca. Citat: Dokazaćemo da ekvivalencija iz postavke ne važi. Uzmimo 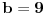 . Da bismo zadovoljili uslov . Da bismo zadovoljili uslov 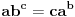 , možemo birati , možemo birati 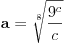 (direktno se proverava). Dakle, dovoljno je još pokazati da postoji (direktno se proverava). Dakle, dovoljno je još pokazati da postoji  takvo da važi takvo da važi 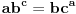 , tj. , tj. 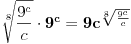 . Posmatrajmo funkciju . Posmatrajmo funkciju 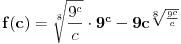 . Ova funkcija očito je neprekidna za . Ova funkcija očito je neprekidna za 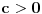 . Dalje, važi . Dalje, važi 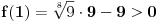 i i 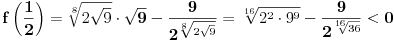 (poslednja nejednakost može se proveriti uz malo dosadnog, „pipavog“, ali ne previše teškog računa). Dakle, postoji (poslednja nejednakost može se proveriti uz malo dosadnog, „pipavog“, ali ne previše teškog računa). Dakle, postoji 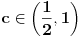 za koje važi za koje važi 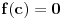 , što je i trebalo dokazati. , što je i trebalo dokazati.Približne vrednosti: 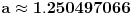 , , 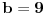 , , 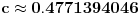 . .[ holononi @ 21.06.2010. 18:01 ] @
Hvala na savetu ali moram da primetim da to što pišeš nema veze sa zadatkom. I ne znam zašto razvodnjavaš temu. Obriši višak posta da ne skrećemo sa teme. Naivno je smatrati da ja ne znam šta je dokaz. Ja ovde ne polažem nikome račune. Ko ima bolji dokaz neka ga iznese.
Elementarno je da linearna, stepena i eksponencijalna funkcija imaju različite priraštaje za istu promenu argumenta. Ja sam iz toga izveo zaključak kako sam izveo. Ako neko ima drukčiji dokaz neka ga iznese. Isto tako možete pobijati stav o priraštajima od koga sam krenuo ali ne možete reći "nije dokaz" jer taj "nedokaz" niste oborili pukom tvrdnjom "nije dokaz". [ holononi @ 21.06.2010. 18:44 ] @
I još nešto. Kako si došao do toga da je c~0.48 i c iz intervala (1/2, 1)?
[ Bojan Basic @ 21.06.2010. 19:19 ] @
Citat: holononi: Hvala na savetu ali moram da primetim da to što pišeš nema veze sa zadatkom. Nema veze sa zadatkom, ali ima veze s onim tvojim tekstom za koji tvrdiš da predstavlja dokaz tvrđenja zadatka. Ako je ono tvoje stvarno dokaz dotičnog tvrđenja, onda je ono moje dokaz velike Fermaove teoreme. Citat: holononi: Ko ima bolji dokaz neka ga iznese. Nije se tražio bolji dokaz, tražio se korektan dokaz. Tvoj nije, pa se ne ubraja u dokaze. U međuvremenu sam ponudio kontraprimer, pa je postalo jasno da dokaz tvrđenja kojim si se ti bavio i ne postoji. No, ta „sitnica“, činjenica da tvrđenje koje pokušavaš dokazati nije tačno, tebe ne sprečava da i dalje tvrdiš kako je tvoj „dokaz“ korektan — neverovatno! Jesi li uopšte svestan šta govoriš? Vraćamo se na početak moje prošle poruke — očito ne znaš značenje pojma dokaz. Citat: holononi: Elementarno je da linearna, stepena i eksponencijalna funkcija imaju različite priraštaje za istu promenu argumenta. Nije tačno (bar ne tako kako si ti zamislio). Evo, 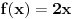 (linearna funkcija) i (linearna funkcija) i 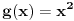 (stepena funkcija). Posmatrajmo tačku (stepena funkcija). Posmatrajmo tačku  (u njoj važi (u njoj važi 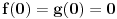 ) i priraštaj ) i priraštaj 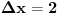 . Tada imamo . Tada imamo 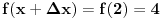 i i 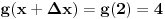 , pa važi , pa važi  . Šta ćemo sad? . Šta ćemo sad?Citat: holononi: ne možete reći "nije dokaz" jer taj "nedokaz" niste oborili pukom tvrdnjom "nije dokaz". OK. Nije dokaz zato što nije svaki korak matematički utemeljen. Je l’ sad u redu? Citat: holononi: Kako si došao do toga da je c~0.48 i c iz intervala (1/2, 1)? Loš primer, zahvaljujem na primedbi. Primer koji bi odgovarao rešenju koje sam napisao jeste 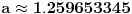 , , 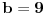 i i 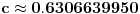 . (Naravno, ove približne vrednosti same po sebi ne znače mnogo, suština je u priči koja je prethodila. Približne vrednosti su tu samo radi lakšeg poimanja.) . (Naravno, ove približne vrednosti same po sebi ne znače mnogo, suština je u priči koja je prethodila. Približne vrednosti su tu samo radi lakšeg poimanja.)[ holononi @ 21.06.2010. 21:04 ] @
Problem je što vi u svojim diskusijama proizvoljno prišivate ljudima šta hoćete. Ovde
http://www.elitesecurity.org/t402777-0#2629759 sam izneo procenu a ne spominje se "dokaz". Drugi su tražili dokaz ali su za sebe zadržavali pravo da diskutuju bez dokaza. Zašto bih ja bio uskraćen za to pravo? Tako i ti izmišljaš da sam ja tvrdio da je "moj dokaz korektan". Ja samo pišem šta sam razmišljao a nisam tvrdio da sam dokazao. Pronadji "onaj moj tekst" u kome "tvrdim da predstavlja dokaz tvrđenja zadatka" [ Nedeljko @ 21.06.2010. 22:05 ] @
Iz onoga što si pisao se jasno vidi da si to navodio kao rešenje. Ja sam se sa svojim "rešenjem" jasno ogradio od toga da je to konačno rešenje time da tu treba još nešto da se dokaže. Diskusija je nešto sasvim drugo od navođenja kao dokaza nečega što nije dokaz.
[ holononi @ 22.06.2010. 08:49 ] @
Šta vi imate meni da dokazujete?
Nisam ja postavio zadatak. Nisam ja tvrdio da Nedeljkovo rešenje (koje takodje nije rešenje) nevalja. Nisam ja bilo kome osporio bilo šta. Jednostavno sam ispisao svoju procenu bez mlaćenja prazne slame po bilo kome. Ko je imao rešenje mogao je da ga ispiše baš kao što sam i ja ispisao ne pominjući nikoga. Naravno, to ne znači da niko ne sme da se osvrće na moje komentare i da ih osporava. Svakako da može jer i ja volim da čujem kritiku mog rada ali u meri i način koja odslikava uljudno ponašanje. Ovako, rešavanje zadatka je postalo sredstvo za nekulturno etiketiranje. Svi su imali priliku da reše zadatak ali umesto da reše zadatak (što je cilj foruma) neki su se pretvorili u pse lutalice. Uzgred, osim neobaveznog ćaskanja i "filozofiranja" upuštanje u detaljnije rešavanje zadatka je uvek sumnjivo i ne odražava preteranu inteligenciju. Motiv da se tako nešto radi besplatno je pre svega nedostatak ličnosti kao što je i etiketiranje odraz nedostatka ličnosti. Zato i pokušaj da se nekom dokaže bilo šta što nije pitao nije ništa drugo nego nedostatak ličnosti. Takvi neka se istresaju na nekom drugom moliću lepo. [ Nedeljko @ 22.06.2010. 09:28 ] @
Napisao si nešto što nije rešenje, navodeći da je kompletno rešenje. Čak si i pitao "šta tu treba da se dokazuje". Na kraju, kada se ispostavilo da nisi u pravu, očigledno si imao problem sa suočavanjem sa tom činjenicom (što bi neki rekli, nedostatak ličnosti) i zato nastavljaš sa ovakvim glupostima. DEa si napisao "uh, da zeznuo sam se" ili da ništa nisi napisao, to bi bila sasvim druga stvar. Ovako, osporavanje tvog rešenja ispada (po tvome) kao napad na tvoju ličnost.
[ holononi @ 22.06.2010. 09:34 ] @
Sad si i ti počeo da izmišljaš. Gde sam ja naveo "da je kompletno rešenje"? Da možda ne "praviš dimnu zavesu"?
[ Nedeljko @ 22.06.2010. 11:27 ] @
Celo vreme si u tom fazonu. No, ovde se niko nije bavio tobom lično, već rešenjem koje si ponudio, čemu valjda forum i služi.
OK, zeznuli smo se obojica (jer se zadatak nije mogao rešiti ni mojim pristupom), ali nemoj zbog toga da se blamiraš. [ holononi @ 22.06.2010. 12:57 ] @
Niko se ne bavi osim tebe i ostalih.
Kako sam primetio da tvoje rešenje nije uredno ja sam izneo procenu a da pritome nisam pljuvao ni po tebi ni po bilo kome drugom. Problem je što vi rešavate zadatak meni a ne onome ko je postavio zadatak. Nema razloga da meni neko bilo šta objašnjava osim ako time taj neko ne leči svoje frustracije. A ja naplaćujem lečenje fustracija. [ Nedeljko @ 22.06.2010. 13:23 ] @
Niko nije pljuvao po tebi. Druga je stvar što kritiku tvog rešenja ti doživljavaš lično. Naravfno da je iz priloženog jasno da smatraš da si najpametniji i da tebi nema ko šta da objašnjava, ali forum služi za diskusiju onih koji žele da učestvuju, dok ostali ne moraju ni da se javljaju. Takođe, postavljaču teme je potrebno ukazati da neko od ponuđenih rešenja nije dobro.
[ holononi @ 22.06.2010. 13:37 ] @
A da tu smo, "smatraš da si najpametniji". Obrati se nekom psihologu i on će ti objasniti da ti ne možeš znati šta ja smatram ali možeš projektovati svoje "smatranje".
Sve smo objasnili, što se mene tiče tema može u arhivu. Hvala na strpljenju i nemojte zameriti. [ Nedeljko @ 22.06.2010. 13:41 ] @
Citat: holononi: Obrati se nekom psihologu i on će ti objasniti da ti ne možeš znati šta ja smatram ali možeš projektovati svoje "smatranje". Da, niko ne može da pronikne u dubinu ove veleumne rečenice: Citat: holononi: Nema razloga da meni neko bilo šta objašnjava Pametnije bi ti bilo da prestaneš da se blamiraš. [ Mali Misha @ 22.06.2010. 13:46 ] @
holononi, čim ti neko kaže da ti je "argumentacija šuplja" i u sledećoj rečenici spomene ludilo, jasno ti je da razgovaraš sa ljudima koji ne biraju mnogo reči.
To i jeste problem, što se od pogrešnog/nepotpunog rešenja pravi velika dževa i prelazi se granica pristojnosti, umesto da se elegantno spusti pod tepih i produži dalje. A da vidiš kako samo isti ti divljaju i brane se do poslednjeg kada se pokaže da je nešto (što su oni radili ili branili) nepotpuno. Zaključavaju teme i brišu poruke koje njihove nebuloze nazivaju pravim imenom. [ Nedeljko @ 22.06.2010. 13:59 ] @
O ličnim osobinama (inteligenciji, nedostatku ličnosti, frustriranosti itd.) je upravo raspravljao holononi i niko drugi. Ko je ovde pomenuo ludilo?
Ja nisam moderator, pa ne mogu ni da brišem tuđe poruke, ni d azaključavam teme. Bojan mi je rekao da je tvoju poruku obrisao jer si prešao na lični plan, mada sam mu ja napomenuo da u toj poruci nisam našao ništa uvredljivo (jer mi je poruka stigla na meil pre nego što je obrisana). A što se tiče tvoje argumentacije o potpunosti rešenja, lično si ti izbegao da odgovoriš na postavljena pitanja i nastavio sa "argumentacijom" u stilu "Ja sam ovde profesor i tako je kako ja kažem". [ Cabo @ 22.06.2010. 15:20 ] @
LOL, kao mala deca ste.
Ljudi da vas gledaju pa da se smeju matematičarima. [ Nedeljko @ 22.06.2010. 23:49 ] @
Evo kompletnog rešenja bez računanja numeričkih vrednosti:
U slučaju da je 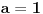 postavka se svodi na postavka se svodi na 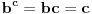 , odakle se lako zaključuje da mora biti , odakle se lako zaključuje da mora biti 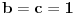 . Stoga razmotrimo slučaj kada je . Stoga razmotrimo slučaj kada je 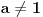 . .Obzirom da mora biti 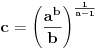 , funkciju po , funkciju po 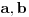 sa desne strane jednakosti označavaćemo sa c. sa desne strane jednakosti označavaćemo sa c.Neka je  jako veliko i jako veliko i 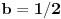 . Obzirom na . Obzirom na 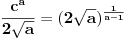 , vrednost , vrednost 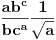 je bliska jedinici, pa je je bliska jedinici, pa je 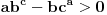 . .Za tako izabrano veliko  može se izabrati može se izabrati  dovoljno blisko nuli da važi dovoljno blisko nuli da važi 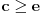 , pa zbog , pa zbog 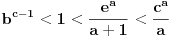 važi važi 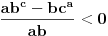 , odakle je , odakle je 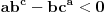 . .Stoga za dovoljno veliko  postoji postoji 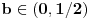 takvo da je takvo da je 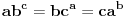 . .[ holononi @ 25.06.2010. 10:21 ] @
U Basicevom rešenju ne može biti f(1)>0.
[ holononi @ 25.06.2010. 12:25 ] @
Za Nedeljka: ako je b=1/2 kako b element (0, 1/2)?
[ Nedeljko @ 25.06.2010. 15:01 ] @
[ holononi @ 25.06.2010. 17:04 ] @
Dobro, Nedeljko je izabrao b iz intervala (0, 1/2) koje zadovoljava prvu jednakost abc = bca. Još dokazati da upravo to b zadovoljava i drugu jednakost.
[ Nedeljko @ 25.06.2010. 17:31 ] @
[ holononi @ 26.06.2010. 08:34 ] @
Pa šta znam, Bašić polazi od netačne pretpostavke f(1)>0 i dolazi do istog zaključka. Stičem utisak da se može pretpostaviti šta ko hoće i doći do želljenog zaključka. Kod tebe se javlja "dovoljno veliko a". Koliko je veliko to a ? Da li je a < 1, a > 1, 1 < a < c ili a > c > 1, da li c > 1 ili c < 1 ?
[ Bojan Basic @ 26.06.2010. 10:00 ] @
[ holononi @ 26.06.2010. 10:13 ] @
Ja ne umem ovo da izračunam
(9^1/1)^(1/8) * 9^1 - 9*1*(9^1/1)^(1/8) i uvek dobijemn da nije veće od 0. [ Nedeljko @ 26.06.2010. 11:48 ] @
(9^1/2)^(1/8)*9-9=2.844666116572...
Nisi dobro prepisao funkciju. [ holononi @ 26.06.2010. 12:39 ] @
Greška postoji u prepisivanju ali ne moja. Ovde
http://www.elitesecurity.org/t402777-1#2630400 lepo stoji f(c) = (9^c/c)^(1/8) * 9^c - 9*c*(9^c/c)^(1/8) pa ne može biti f(c)>0 za c=1. [ Nedeljko @ 26.06.2010. 14:02 ] @
f(c) = (9^c/c)^(1/8) * 9^c - 9*c^((9^c/c)^(1/8))
Ispravljeno. Dakle, b=9, c=1, a=(b^c/c)^(1/(b-1))=9^(1/8) ab^c-bc^a=9^(9/8)-9>0. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|