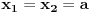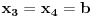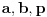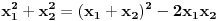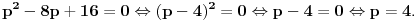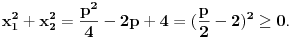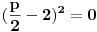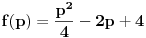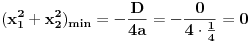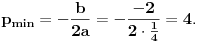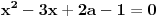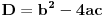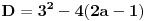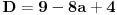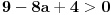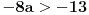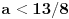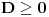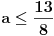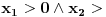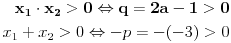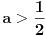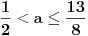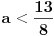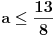[ ainspirationN @ 19.06.2010. 05:58 ] @
| Pozdrav za sve na forumu. Treba mi pomoc oko dva zadataka sa vijetovim pravilima...svaka pomoc ili savet mi je dobrodosao.... http://img42.imageshack.us/img42/7004/38391359.jpg Prvi zadatak pod a mi je jasan..da bi jednacina imala dve jednake nule treba da bude D=0 ... dobijem da je p=-2 i p=0.... pod b) mi nije jasano a kontam da je nesto jednostavno.... Drugi mi zadatak uopste nije jasan..da li ja treba da nadjem interval u kojem je minimalan ili tacku..? |