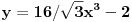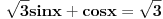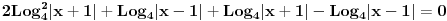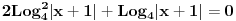[ LogX @ 21.06.2010. 11:09 ] @
|
[ bobanex @ 21.06.2010. 13:22 ] @
1.
a+aq+aq^2=91 a+25+aq^2+1=2(aq+27) resi sistem, uzmi u obzir da je niz rastuci pri odredjivanju q, posle ces lako naci sedmi clan. 4. (sqrt(3)/2)sinx+(1/2)cosx=sqrt(3)/2 cos(pi/6)sinx+sin(pi/6)cosx=sqrt(3)/2 sin(x+pi/6)=sqrt(3)/2 ... [ Cabo @ 21.06.2010. 15:33 ] @
Glavni problem kod izraza tipa:
Citat: LogX: 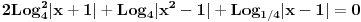 je što se ljudi demorališu kad vide „šumu“ simbola. Samo polako i pažljivo, korak po korak, i rešićeš. Zadatak uopšte nije težak, samo iziskuje dosta strpljenja i: vremena ili iskustva. [ LogX @ 21.06.2010. 17:45 ] @
neverovatno da se nisam setio da postavim takav sistem. Hvala.
Sto se tice logaritama,u sustini glavna stvar je prvo postaviti uslove jel da? [ bobanex @ 21.06.2010. 21:23 ] @
[ miki069 @ 21.06.2010. 21:35 ] @
3.Najmanja vrednost rastojanja tacke M(0,-2) od tacaka (x;y) takvih da je...uslov.
d = koren((x-0)^2 + (y+2)^2) Tražiš funkciji d ektremne vrednosti (minimum). Formraš Lagranžovu funkciju: F(x,y,p) = d(x,y) + p*(uslov) p je parametar. Dalje znaš? Ili praktičnije rešenje je da u izraz d = koren((x-0)^2 + (y+2)^2) direktno zameniš y iz uslova i dobiješ d u funkciji samo od x. d = koren(x^2 + (256/3)*x^6) i nađeš joj minimum. Dalje znaš? [Ovu poruku je menjao miki069 dana 21.06.2010. u 22:50 GMT+1] [ LogX @ 21.06.2010. 21:44 ] @
Citat: miki069: 3.Najmanja vrednost rastojanja tacke M(0,-2) od tacaka (x;y) takvih da je...uslov. d = koren((x-0)^2 + (y+2)^2) Tražiš funkciji d ektremne vrednosti (minimum). Formraš Lagranžovu funkciju: F(x,y,p) = d(x,y) + p*(uslov) p je parametar. Dalje znaš? Ako nesto zapne javicu . Hvala puno. Obicno mi treba samo podstrek kako poceti zadatak a onda mi se javi kako dalje :D [ miki069 @ 21.06.2010. 22:01 ] @
Izjednačavanjem izvoda navedene funkcije sa nula dobija se jedino realno rešenje X=0.
Data tačka M(0,-2) pripada grafiku funkcije iz uslova. (jbg tek sad vidim). Ona je od sebe udaljena nula. Ali ne ispunjava uslove zadatka jer mora biti x>0. Tako da je zadatak filozofski. Koja je to prva tačka do x=0 da ispunjava uslov x>0? [ bobanex @ 21.06.2010. 22:37 ] @
Mozda je postavljac teme slucajno napisao pogresno izraz, a ili b?
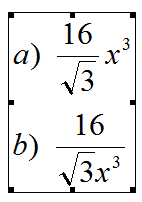 [ LogX @ 22.06.2010. 12:14 ] @
Citat: Pod b :) [ miki069 @ 22.06.2010. 12:45 ] @
Kako pod b) kad množenje i deljenje imaju istu prednost?
Onda staviš zagradu i sve bude jasno. Nema veze, ajd ponovo: Onda tačka M(0,-2) ne pripada funkciji iz uslova i zadatak ima smisla. Onda u izraz d = koren((x-0)^2 + (y+2)^2) direktno zameniš y iz uslova i dobiješ d u funkciji samo od x. Uradiš joj prvi izvod i isti izjednačiš sa nulom... Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|