[ Nikola 23 @ 22.06.2010. 21:28 ] @
Kako se resava ovaj zadatak uopste, sta tacno da uzmemo za k, a sta za n ?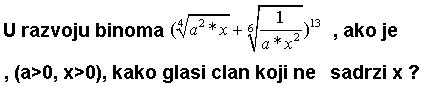 |
|
[ Nikola 23 @ 22.06.2010. 21:28 ] @
[ LogX @ 25.06.2010. 20:17 ] @
Kako glasi ceo zadatak? Po ovome samo se vidi da je n=13 Ne znam jel ti se trazi neki clan ili jos nesto? Trebalo bi da znas osnovnu formulu za neki clan ... Clan koji ne sadrzi x nalazis tako sto na kraju kada sredis clan po formuli ,eksponent koji je uz x izjednacis sa 0.
EDIT : Ustvari verovatno ti se trazi "k" a to ces naci lako samo kad sredis binom preko formule. I na kraju izjednacis eksponent sa nulom naravno gde ce ti biti nepoznato "k" . [Ovu poruku je menjao LogX dana 26.06.2010. u 16:47 GMT+1] [ Cabo @ 28.06.2010. 17:39 ] @
[ Cabo @ 29.06.2010. 16:35 ] @
[ NTManiac @ 29.06.2010. 18:25 ] @
metod ti je dobar... ali je ocito greska u postavci zadatka... ili jednostavno reci da je rjesenje 0
[ Cabo @ 30.06.2010. 14:52 ] @
[ miki069 @ 30.06.2010. 15:29 ] @
Pogrešno prepisan zadatak. Drugi u binomu je peti koren a ne šesti koren.
Kada prvi član ide na 8 srepen a drugi na peti dobije se traženo rešenje. [ holononi @ 30.06.2010. 15:50 ] @
U razvoju binomne formule k ide od 0 do n tj. u ovom slučaju do 13. Ovaj zadatak nije dobro postavljen. Jedino ako misli na članove koji ima "čisto" x, odnosno x^1.
[ Cabo @ 30.06.2010. 16:11 ] @
Citat: holononi: U razvoju binomne formule k ide od 0 do n tj. u ovom slučaju do 13. Ovaj zadatak nije dobro postavljen. Jedino ako misli na članove koji ima "čisto" x, odnosno x^1. Ako je 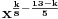 , onda se dobije , onda se dobije 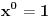 za za 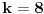 , preko standardne formule. , preko standardne formule.Zadatak je u redu, samo treba da stoji 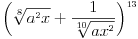 . .I onda je odgovor 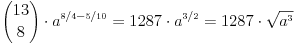 . .[Ovu poruku je menjao Cabo dana 30.06.2010. u 17:40 GMT+1] [ holononi @ 30.06.2010. 16:30 ] @
Ali u zadatku ne stoji osmi koren već četvrti. Dakle "samo".
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|