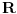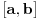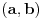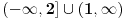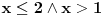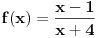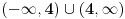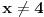[ Maksa12 @ 23.06.2010. 14:48 ] @
Jednacina x^2+2mx-(m-2)=0 ima realna resenja x1 i x2 koja zadovoljavaju uslov 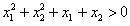 Ja sam nasao Diskriminantu ((2*m)^2-4*(-(m+2))) i po toj formuli sam nasao m. Znam da je parametar m jednak: m=-2 ili m=1 E sad ja imam ponudjena resenja (na slici) od kojih u zbirci treba da zaokruzim jedno: a) 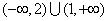 b) 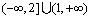 c) 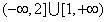 Znam vrednosti parametra m, ali kako da znam koji je od ovih ponudjenih odgovora tacan, odnosno po cemu se razlikuju ti odgovori, kada su im samo vrste zagrada drugaciji, a unutar zagrada je isto u sva 3 ponudjena odgovora. Da li tu postoje neka pravila ili to ipak nije bitno da li su u domenu zagrade ovakve [ ili ovakve ( ? [Ovu poruku je menjao Maksa12 dana 23.06.2010. u 17:28 GMT+1] |