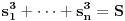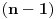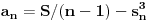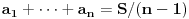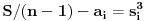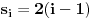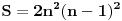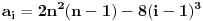[ milutinovicsm @ 27.06.2010. 23:54 ] @
| Zdravo svima! Imam jedan zadatak za koji mi je tesko utvrditi da li ima resenje ili ne,tako da me veoma zanima sta je u stvari resenje.U zadatku se pita da li postoji n razlicitih brojeva,takvih da je suma svakih n-1 (od tih brojeva) potpun kub;ja za n=4 dobijem da to vazi,i pokusao sam da uopstim,samo sto dobijem nesto sto po mom misljenju nije dovoljno dobar dokaz da takvi brojevi postoje. Unapred hvala. |