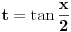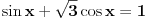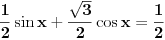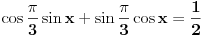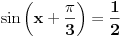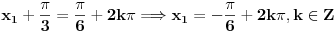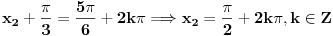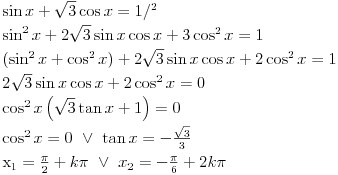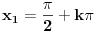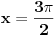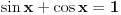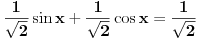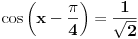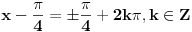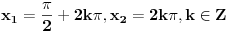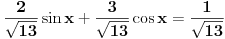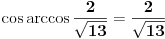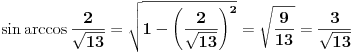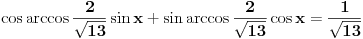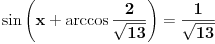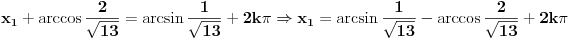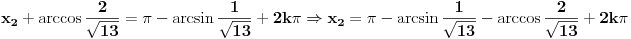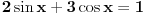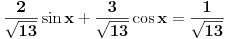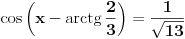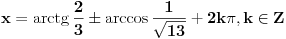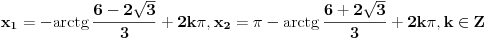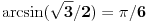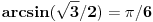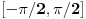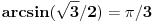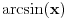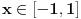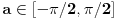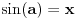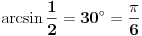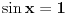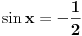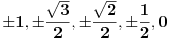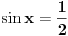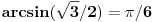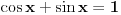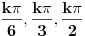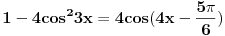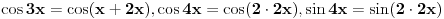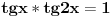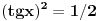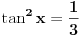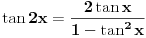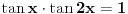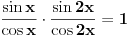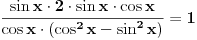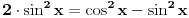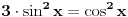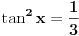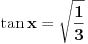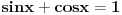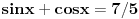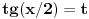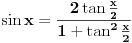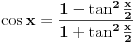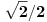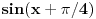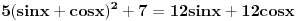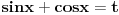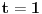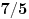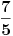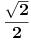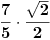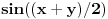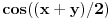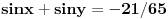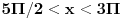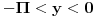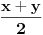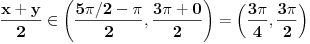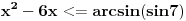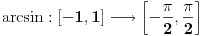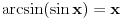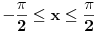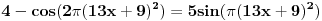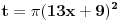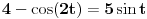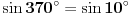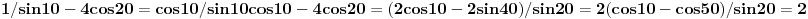[ grabber @ 30.06.2010. 15:56 ] @
|
| Evo mene opet : )
Jos jedan problemcic u vezi prijemnih zadataka, radi se o trigonometrijskoj jednacini u koju JA MISLIM treba uvesti smjenu tg(x/2), ali nisam siguran kako privesti kraju zadatak koji glasi ovako:
 |
[ holononi @ 30.06.2010. 16:24 ] @
Zadatak čak i ja znam da rešim i to pomoću sin2x + cos2x = 1 za minut.
[ grabber @ 30.06.2010. 16:33 ] @
Pokušat ću i tako ako se uspijem snaći :D Jbg izvinjavam se ako postavljam gluposti, ali sada pred prijemni kroz sve 4 godine prelazim, pa malo je sve još uvijek pomiješano :D
[ Farenhajt @ 30.06.2010. 16:46 ] @
[ grabber @ 30.06.2010. 16:57 ] @
OK, hvala puno, evo uradio sam i dobio dva rjesenja:
1) pi/2 + kpi
2) pi/6 + 2kpi
[ Farenhajt @ 30.06.2010. 17:55 ] @
Ne valja ti ni jedno ni drugo rešenje.
[ holononi @ 30.06.2010. 18:43 ] @
Serviranje gotovih rešenja je "medvedja usluga". Mnogo je bolje podsetiti učenika (iz čijih se komentara vidi da se i sam trudi) na to da treba znati neke od osnovnih trigonometrijskih jednakosti.
Matematika u kojoj neko tera učenike da pamte gomilu vrednosti trigonometrijskih funkcija je potrebna u životu isto kao i lanjski sneg. Zato je puki kapric nešto poput "e neznaš koliko je sinus od 23.17 stepene jedan za kraj godine". Mnogo je bolje učiti kako se barata tim formulam jer vrednosti trigonometrijskih funkcija možete očas dobiti iz kalkulatoa koji se nadje na djubrištu.
[ miki069 @ 30.06.2010. 19:34 ] @
Smena tg(x/2)=t ili korišćenje osnovnog trinometrijskog identiteta su mnogo jače metode za rešavanje ovakvih jednačina.
Ovo rešenje je trange-frange. Pomaže u ovom zadatku a u sledećih 999 ne pali.
Recimo, naći sva rešenja:
sin(x) + cos(x) = 1
[ mokelet @ 30.06.2010. 20:28 ] @
Može i ovako (bez da se zna sinus zbira):
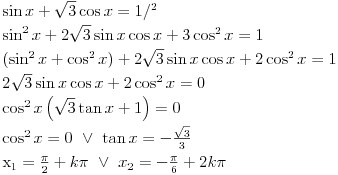
[ Farenhajt @ 30.06.2010. 20:44 ] @
Citat: mokelet: Može i ovako (bez da se zna sinus zbira):
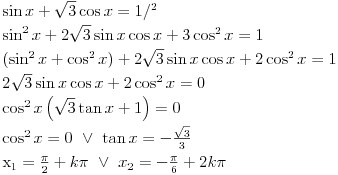
Kao što već rekoh gore, rešenje 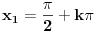 nije ispravno: recimo, za 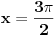 jednačina nije zadovoljena. Ali ko se još uopšte bakće s time da proveri rešenja...
Citat: miki069: Smena tg(x/2)=t ili korišćenje osnovnog trinometrijskog identiteta su mnogo jače metode za rešavanje ovakvih jednačina.
Ovo rešenje je trange-frange. Pomaže u ovom zadatku a u sledećih 999 ne pali.
Recimo, naći sva rešenja:
sin(x) + cos(x) = 1
Uh, što obožavam kad "stručnjaci" pričaju napamet:
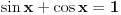
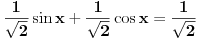
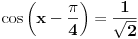
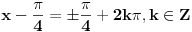
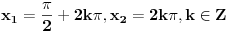
Pojma ti nemaš. Sedi - jedan. [ miki069 @ 30.06.2010. 20:54 ] @
Uradi ta 2 zadatka i sledećih 999 998 komada ćorak:
Ajde demonstriraj na:
2*sin(x) + 3*cos(x) = 1
Upustvo za "stručnjaka" koji deli jednačine: podeli je sa Plankovom kostatnom.
[ mokelet @ 30.06.2010. 20:54 ] @
Hebote, al' ste surovi.
[ Cabo @ 30.06.2010. 21:07 ] @
Vrućina...
[ Bojan Basic @ 30.06.2010. 21:32 ] @
Citat: miki069:
Ajde demonstriraj na:
2*sin(x) + 3*cos(x) = 1
Evo, ja ću.
Citat: miki069:
Upustvo za "stručnjaka" koji deli jednačine: podeli je sa Plankovom kostatnom.
Nema potrebe, biće dovoljno i 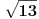 .
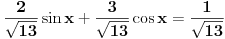
I sada, pošto je 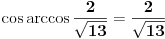 i 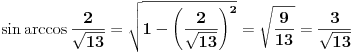 , nastavljamo kao i ranije:
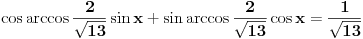
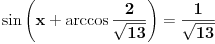
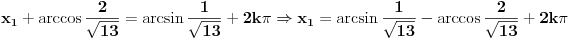
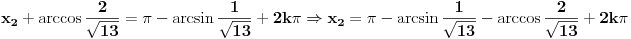
Hoćeš li sad priznati da si nadmeno pričao o stvarima u koje se ne razumeš previše, ili ćeš se prvo ispaliti još nekoliko puta?  [ Farenhajt @ 30.06.2010. 21:36 ] @
Citat: miki069: Uradi ta 2 zadatka i sledećih 999 998 komada ćorak:
Ajde demonstriraj na:
2*sin(x) + 3*cos(x) = 1
Upustvo za "stručnjaka" koji deli jednačine: podeli je sa Plankovom kostatnom.
Gospode bože, kako si žalosno komičan u svom nemoćnom besu neznalice koji bi tako silno želeo da se razbacuje "najjačim metodama"... Dođe čoveku da zaplače...
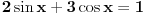
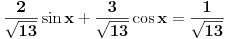
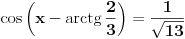
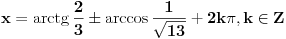
A ako nam je stalo da sredimo ove izraze (ne bih te zadržavao na tome, treba da smišljaš nove nerešive jednačine), dobićemo
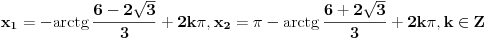 [Ovu poruku je menjao Farenhajt dana 30.06.2010. u 22:56 GMT+1]
[Ovu poruku je menjao Farenhajt dana 30.06.2010. u 22:56 GMT+1][ holononi @ 30.06.2010. 21:58 ] @
[ miki069 @ 01.07.2010. 03:31 ] @
Moja greška (da mi Farenhajt ne zaplače):
Ovo "deljenje" rešava sve jednačine oblika:
a*sin(x) + b*cos(x) = c
Plankova konstanta je koren(a^2 + b^2).
Cilj mi je bio da autora zadatka "usmerim" na pravi put, a ne na "trage-frange" metode.
Za navedeni oblik jednačina , deljenje sa Plankovom konstantom, nije "trange-frange" metoda.
Pošto nema kvadriranja, čak je i bolja, jer se rešenja ne moraju proveravati naknadno.
Isto je moglo biti objašnjeno autoru zadatka.
Bilo bi i meni jasno i ne bih ga "usmeravao".
Ja sam napamet znao kako se rešavaju 4 kombinacije za (a,b) = (1, koren(3)) ili ((koren(3),1) ili (1,1) ili (koren(2), koren(2)).
Drugi zadatak sa (a,b) = (1,1) sam znao napamet.
Treći sa (a,b) = (2,3) nisam znao da uradim, na ovaj način bez kvadriranja, i zato sam i izmislo "Plankovu konstantu".
Mislio sam da ne može i da pije vodu samo za nabrojane slučajeve.
Bojane, Gorane - svaka čast.
Mokelet: posle kvadriranja moraš proveriti sva rešenja jer ne dobijaš ekvivalentnu jednačinu. 3*pi/2 ne zadovoljava jednačinu.
Već ti je Farenhajt sugerisao na to.
[Ovu poruku je menjao miki069 dana 01.07.2010. u 04:49 GMT+1]
[ holononi @ 01.07.2010. 07:19 ] @
2sinx + 3cosx = 1
9cos2x = 1 - 4sinx + 4sin2x
Pa može da se reši kao kvadratna jednačina.
[ miki069 @ 01.07.2010. 07:56 ] @
Može i kao kvadratna jednačina.
Pošto iz prve samo sledi (a nije joj ekvivalentna) druga jednačina, onda sva rešenja moraju da se proveravaju.
[ holononi @ 01.07.2010. 08:45 ] @
To je tačno.
Samo ipak smatram da srednješkolci ne treba da bubaju napamet tablicu vrednosti trigonometrijskih funkcija.
[ Nedeljko @ 01.07.2010. 10:07 ] @
Ali, treba da znaju brzo da je izvedu.
[ holononi @ 01.07.2010. 10:46 ] @
Naravno da treba da raspolažu odredjenom brzinom u baratanju tim formulama. Medjutim, da li se to odnosi i na inverzne funkcije trigonometrijskih funkcija? Možda za učenika matematičke gimnazije, ali šta ćemo sa ostalima? Hoćemo li da ograničimo upis samo na one koji su završili matematičku gimnaziju?
No, iskreno govoreći nisam u ranijim testovima primetio da se zadaci ne mogu rešiti bez korišćenja inverznih trigonometrijskih funkcija. Baš naprotiv, zadaci su "naštimovani" tako da to nije potrebno. Ne znam kako je bilo juče i danas, možda se i tu nešto promenilo.
[ Nedeljko @ 01.07.2010. 11:04 ] @
Jednakosti tipa 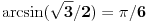 treba da zna svaki gimnazijalac za trojku iz matematike.
P.S. Kao što i sam znaš, trigonometrijske funkcije nisu inverzibilne, pa je pravilnije reći "inverzne trigonometrijske funkcije". [ holononi @ 01.07.2010. 13:25 ] @
Citat: Jednakosti tipa 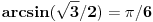 treba da zna svaki gimnazijalac za trojku iz matematike.
Uz napomenu da govorimo o restrikciji na segmentu 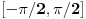 pa postoji inverzna funkcija.
Medjutim, zanima me u kom razredu srednje škole (ne računajući matematičku gimnaziju) se u toj meri rade inverzne funkcije (restrikcija) trigonometrijskim funkcijama tako da bi učenik rešavao zadatak na način kako su predložili neki diskutanti. Za kvadratnu jednačinu i osnovne trigonometrijske identitete sam ubedjen da svi prodju i to u dosta zadataka.
Da li hoćeš da kažeš da ti daješ trojku ako učenik zna vrednost 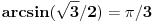 ? (PS. neću da komentarišem tipografske greške koje si napravio).
Ili hoćeš da kažeš da ne može da ima više od 2 ako to ne zna a zna recimo da rešava integrale ? [ Nedeljko @ 01.07.2010. 13:47 ] @
Ne predajem, ali govorim kako je bilo kad sam ja bio u školi (nije elitna).
Iz trigonometrije ne treba da dobije više od dva onaj ko ne zna da je 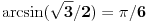 .
Pojam funkcije, domena i inverza se rade u prvom rayredu na pošetku. Pod sinusom se obično podrazumeva funkcija definisana i za tupe uglove npr. pa svakako nije inverzibilna. Za restrikciju je OK za one koji to znaju kako treba. Obzirom da se inverzne trigonometrijske funkcije uče, trebalo bi da se uče kako treba. 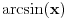 za 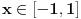 je takvo 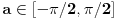 za koje je 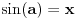 , npr. Tako bi trebalo da se uči. [ holononi @ 01.07.2010. 13:52 ] @
Pa koliko si ti imao iz trigonometrije (ako nije tajna) ?
[ Nedeljko @ 01.07.2010. 14:21 ] @
Nije tajna. Ne sećam se, ali sam uvek znao da izvedem sve formule koje mi trebaju.
[ holononi @ 01.07.2010. 14:25 ] @
U medjuvremenu si izgleda po malo zaboravio.
[ Nedeljko @ 01.07.2010. 14:42 ] @
Šta sam zaboravio?
[ holononi @ 01.07.2010. 15:07 ] @
Pa šta znam, kad sam ja išao u školu sin(Pi/6) je bilo 1/2.
[ Nedeljko @ 01.07.2010. 18:00 ] @
Ah, da. Napisao sam brzopleto. Hvala na ispravci.
[ Farenhajt @ 01.07.2010. 20:57 ] @
Načelno se slažem s Nedeljkom. Štaviše, klinci se već u, čini mi se, sedmom razredu sreću s ČINJENICOM da ako je hipotenuza pravouglog trougla dvaput veća od jedne katete, onda je taj trougao polovina jednakostraničnog trougla, tj. ima uglove od 30, 60 i 90 stepeni. Prema tome, ako je ta ČINJENICA prisutna u njihovom znanju znatno pre nego što joj se "obuče odeća" oblika 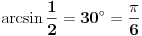 , onda nema opravdanja da se i ta "odeća" ne nauči tokom čitave srednje škole. [ holononi @ 01.07.2010. 21:51 ] @
U redovnoj nastavi srednje škole zadaci se ne rešavaju primenom arkus funkcija. Svako rešenje koje se zasniva na primeni tih funkcija za učenika može biti neprihvatljivo. Zato se rešenja moraju zasnivati na primeni osnovnih trigonometrijskih identiteta, adicionih formula i formula dvostrukog ugla.
[ Farenhajt @ 01.07.2010. 22:25 ] @
Malo si se zaneo. Apsolutno SVAKA tringonometrijska jednačina rešava se primenom arkus funkcija: čak si i ti, u svom rešenju preko kvadratne jednačine, na kraju morao da pretvoriš 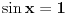 i 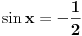 u nekakve uglove, a kako se to radi? Primenom arkus funkcija.
Samo što se to na nivou opšte srednje škole tako NE ZOVE (tj. nema "odeću"). Shodno tome, brojevi u zadacima se lepo štimuju, a servira se tablica "lepih" vrednosti za "lepe" uglove ( 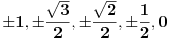 ), koja se stoga mora ili zapamtiti ili stalno u glavi imati povezana s jednakostraničnim odnosno jednakokrako-pravouglim trouglom.
No bilo kako bilo, činjenica ostaje da srednjoškolci stalno primenjuju arkus funkcije, počev od boza-jednačine tipa 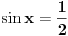 , ali ih tako ne zovu.
[Ovu poruku je menjao Farenhajt dana 01.07.2010. u 23:52 GMT+1][ Nedeljko @ 01.07.2010. 22:35 ] @
Nije mi baš najjasnije zašto se u srednjoj školi ne uče arkus funkcije. Mi smo čak računali njihove izvode i učili razvoj arkustangensa u Tejlorov red.
[ holononi @ 02.07.2010. 06:44 ] @
Nisam se zaneo. Jedno je napisati x = arcsin(t) a sasvim drugo baratati tim funkcijama. Možete mi dokazivati šta god hoćete ali stanje je takvo kakvo je, te funkcije se ne obradjuju (osim što se pomenu) u srednjoj školi. Od srednješkolca je prihvatljivo da napiše x = arcsin(1/2) i to je rešenje. A ako se još seti da je sin(pi/6) = 1/2 pa dobro, još bolje, medjutim ne postoji obaveza jer bi to onda bilo pamćenje napamet gomila činjenica a upravo se zalažemo za nešto drugo, kreativnost. Inače na prijemnom je dozvoljeno korišćenje kalkulatora pa učenik može odrediti i ugao ako se baš traži u zadatku.
Na pitanje "zašto je to tako?" odgovor je "zašto bi bilo drukčije?". Svi se žale da su nastavni planovi i programi preobimni.
[ holononi @ 02.07.2010. 06:51 ] @
Za Nedeljka: Znao si razvoj funkcije u Tejlorov red, a da li si znao recimo oksidativno fosforilovanje ili da li si znao proteohormone? To danas znaju gimnazijalci.
[ Nedeljko @ 02.07.2010. 09:30 ] @
Osnovne vrednosti trigonometrijskih funkcija se mogu izvoditi, a ne moraju pamtiti.
[ Cabo @ 02.07.2010. 13:17 ] @
Štaviše, meni je daleeeeeeeko lakše (a i tačnije) da nacrtam trigonometrijski krug i onda odatle gledam vrednosti sinusa, kosinusa, itd.
[ holononi @ 02.07.2010. 14:45 ] @
Aha, ubedili ste me.
Citat: Jednakosti tipa 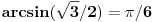 treba da zna svaki gimnazijalac za trojku iz matematike.
Medjutim vas trojke nisu zanimale zar ne ? [ Cabo @ 02.07.2010. 14:57 ] @
[ holononi @ 02.07.2010. 15:19 ] @
Pa dobro, navedite udžbenik matematike za srednju školu u kome se zadaci ovog tipa rešavaju primenom arkus funkcija kako su neki prezentovali.
[ Cabo @ 02.07.2010. 15:27 ] @
Zavisi od toga šta znači „primena arkus funkcija“. Nama je profa dao da fotokopiramo „puškicu“ sa osnovnim vrednostima sinusa, kosinusa, ali i trigonometrijskim krugom, adicionim formulama... koristili smo je na času, a na kontrolnom, naravno, nije bila dozvoljena.
[ holononi @ 02.07.2010. 16:18 ] @
Citat: Zavisi od toga šta znači „primena arkus funkcija“.
I vi ste u srednjoj školi tako rešavali taj tip zadataka ? [ Cabo @ 02.07.2010. 16:54 ] @
Ne sećam se baš najbolje. :-S
Mislim da smo radili i inverzne trigonometrijske funkcije, ali su mi posle godina studiranja matematike detalji u vezi sa time šta se tačno radilo u srednjoj školi magloviti.
[ holononi @ 02.07.2010. 17:49 ] @
Radili ste, kod tabličnih integrala. To se i danas radi. I na tome uglanom ostaje.
[ Bojan Basic @ 03.07.2010. 13:32 ] @
Taj zadatak apsolutno je nemoguće rešiti bez primene inverznih trigonometrijskih funkcija (kojim god metodom), jer se rešenje ne može egzaktno izračunati već se mora izraziti preko njih. Ako tvrdiš drugačije, molim te da rešiš zadatak na koji god način hoćeš, ali bez pomena inverznih trigonometrijskih funkcija. [ holononi @ 03.07.2010. 15:46 ] @
Jedno je znati na kalkuklatoru odrediti sin -1(0.5) a sasvim drugo primenjivati arcsin na rešavanje zadataka. Ti si u svom rešenju više puta primenio arkus funkcije i to na način za koji je potrebno dosta veštine. Medjutim u srednjoj školi se arkus funkcije rade samo informativno tako da je rešenje nerazumljivo srednješkolcu izuzimajući one koji idu u specijalna odeljenja ili sekcije. Uostalom nisam nikad video na prijemnom zadatak koji se nije mogao rešiti primenom elementarnih trigonometrijskih identiteta kao što je na primer ovaj
http://www.elitesecurity.org/t403869-0#2638379
Ako neko zna za zadatak sa prijemnog koji se mora rešavati na način koji si ti predložio neka ga postavi da ubuduće skrenemo pažnju učenicima na takve detalje.
[ Farenhajt @ 04.07.2010. 00:08 ] @
Opet si zastranio. Zadatak od koga nikako da se odlepiš nije ovde uopšte naveden kao tipičan primer srednjoškolskog problema (dakle, kao nešto za frontalnu nastavu u nespecijalizovanom odeljenju/školi), nego ga je miki069 dao kao pokušaj "utuka na utuk" dok je imao ekspoze o najjačim metodama. Prema tome, zadatku namera i NIJE bila da ukaže da opšti nivo, nego da bude tvrd orah na kome će znalci "slomiti zube", ali se to, jelte, nije desilo...
Dva zadatka koji JESU primereni za frontalnu nastavu u nespecijalizovanom odeljenju/školi navedeni su pre toga, i umeo bi da ih reši svaki đak koji znanjem dobacuje bar do jake trojke, tj. onaj ko zna tablicu osnovnih vrednosti i adicione formule.
A sad "idi malo stani tamo."
[ holononi @ 04.07.2010. 09:06 ] @
Zadatak nije postavio miki069 već graber
http://www.elitesecurity.org/t403869-0#2638043
Jasno se vidi da učenik priprema prijemni ispit
Citat: u vezi prijemnih zadataka
Zato se ne radi o zadatku koji treba "da bude tvrd orah na kome će znalci "slomiti zube"" već baš naprotiv. Zadatak je za "opšti nivo".
Inače sam zadatak ne povlači organizacioni oblik nastavnog rada. Organizacioni oblik nastavnog rada zavisi od medjusobnih odnosa nastavnika i učenika u pojedinim nastavnim situacijama. Tako i ovaj zadatak može da se rešava različitom organizacijom nastavnog rada na času. Ali ono što mora to je da se oslanja na prethodna znanja učenika. [ Farenhajt @ 04.07.2010. 16:18 ] @
Alo, dečko, šta bulazniš??
Grabber je postavio 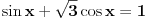 , što je na redovnom nivou srednje škole.
Onda je miki069 postavio 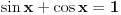 , u pokušaju da dezavuiše metodu svođenja na adicionu formulu. Ispostavilo se, međutim, da je i taj zadatak na redovnom nivou srednje škole: štaviše je još lakši nego prethodni.
Onda je miki069 u "besu" postavio 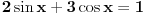 što nije na nivou onih srednjih škola u kojima se ne uče arkus funkcije.
Izvoli pregledaj temu kako bi se uverio da jeste tako kako kažem, a onda ZAISTA umukni. [ Nedeljko @ 04.07.2010. 16:42 ] @
Zamolio bih te da pripaziš na izražavanje. Ovo ipak nije avocacy.
[ Farenhajt @ 04.07.2010. 16:58 ] @
E samo nek si se TI našao da me opominješ za izražavanje. Šta ću sve dočekati...
Uzgred, nije mi poznat taj termin "avocacy".
[ holononi @ 04.07.2010. 17:10 ] @
Ako neko rešava mikijeve zadatke neka se ne obraća meni. U komentaru nakon koga mi se Farenhajt obratio jasno stoji link na rešenje koje sam ispisao.

I Farenhajt lepo kaže
Citat: Zadatak od koga nikako da se odlepiš
Da to je zadatak o kome ja govorim i na koji ti tvrdiš da sam "zastranio" i tvrdiš da je to tipičan primer za "frontalnu nastavu". Zato sam odgovori to što sam odgovorio.
Medjutim, ja sam uvek strpljiv u podučavanju pa ću ponoviti: arkus funkcije se u srednjoj školi ne rade u dovoljnom obimu da bi učenik stekao veštinu da rešava ovakve zadatke njihovom primenom. Zadaci na prijemnom ispitu su dati tako da se proveri da li je učenik savladao osnovne trigonometrijske idetitete. Zato se od učenika pre svega očekuje da zadatke rešava primenom tih idetiteta. Osnovni trigonometrijski identiteti se detaljno obradjuju još od drugog razreda i uvode se metodološki tako da je to donja crta ispod koje se ne ide i nema opravdanja ako ih neko ne zna.
Zato ja apsolutno preporučujem učenicima kada se pripremaju za prijemni da OBAVEZNO ponove osnovne trigonometrijske identitete, funkcije dvostrukog ugla i adicione formule.
[ Nedeljko @ 04.07.2010. 17:56 ] @
Citat: Farenhajt: E samo nek si se TI našao da me opominješ za izražavanje. Šta ću sve dočekati...
Uzgred, nije mi poznat taj termin "avocacy".
Advocacy je jedan od ES foruma. Što, kome sam ja rekao da bulazni? Kako se ja to izražavam? Daj neki citat. [ Farenhajt @ 04.07.2010. 18:08 ] @
Da, apsolutno tvrdim da taj zadatak i zadatak 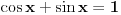 JESU za frontalnu nastavu, i to metodom koju sam prezentirao na primerima ta dva zadatka, pošto:
1. Adicione formule JESU gradivo za frontalnu nastavu;
2. Tablične vrednosti funkcija za uglove 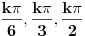 , kao i vladanje tim tabličnim vrednostima U OBA SMERA, JESU gradivo za frontalnu nastavu.
Ko ne zna bilo stavku 1 bilo stavku 2 (pri čemu pod "znanjem" podrazumevam prepoznavanje i praktično primenjivanje tih stavki, a ne golo bubecanje i mehaničko ispisivanje kredom na tabli bez ikakvog razumevanja čemu to služi), ne treba da očekuje iole bolju ocenu iz trigonometrije. [ holononi @ 04.07.2010. 18:45 ] @
Iz toga što se te metode mogu obraditi frontalnim radom može da se zaključi samo da će nastavnik tako najracionalnije upotrebiti trud i vreme i ništa više. Primena frontalnog rada ne donosi učeniku posebne prednosti.
Ako neko hoće da kaže da sve što se obradi frontalnim radom učenik mora znati na nivou primene onda me zanima kako bi se sve te metode uspešno obradile ako se ima u vidu da je nastava matematike u nekim školama manje od 5 časova nedeljno, sa četiri ili čak tri časa nedeljno. Ako bi se insistiralo na posebnim metodama rešavanja zadataka onda je prijemni ispit nepotreban. Jednostavno rangirate na vrh liste one koji su imali više nastave matematike. No takve liste u praksi su neadekvatne čak i kad uzmete ocene iz srednje škole. Mnogi vukovci ne prodju ni cenzus dok na budžet udju učenici koji i nisu bili "mamini i tatini kćeri i sinovi".
[ devetkamp @ 09.01.2012. 19:40 ] @
Jel bi mi dao neko ideju kako da resim sledecu jednacinu: 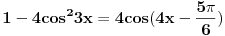 . Hvala. [ Sonec @ 09.01.2012. 19:55 ] @
Pa uvek moze da prodje razvijanjem 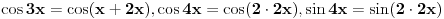 , itd, itd, al verovatno da postoji laksi nacin. [ devetkamp @ 09.01.2012. 20:07 ] @
Danima lupam glavom i nista mi ne pada na pamet. Verovatno postoji, ali ko ce ga znati....
[ cikin @ 10.01.2012. 16:38 ] @
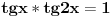 e kako god da radim meni ispada 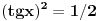 nznm gde gresim [ Sonec @ 10.01.2012. 16:54 ] @
Pa proveri jos jednom racun, stvarno je lako.
Dobija se 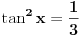
Koristis (a verujem da i jesi) 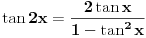 [ Sherlock Holmes @ 10.01.2012. 17:00 ] @
[ cikin @ 09.03.2012. 19:55 ] @
e imam zadatak i sad 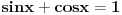 a drugo resenje mi je 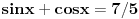 .... ovo kad je jedan to znam, e al u drugom u resenju mi pise da koristim 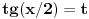 ako moze neka pomoc.... [ Sonec @ 09.03.2012. 19:59 ] @
[ darkosos @ 09.03.2012. 20:06 ] @
To 7/5 mi nesto sumnjivo... Kad se pomnozi leva strana sa 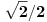 dobija se 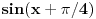 sto tesko moze da se nategne na 7/5... [ cikin @ 09.03.2012. 20:12 ] @
evo ceo zadatak 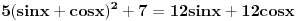 e sad zamenio 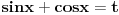 resio i dobio da je 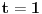 za 1 sam uradio, a drugo resenje je 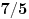 napisali su da su menjali 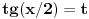 [ Sonec @ 09.03.2012. 20:14 ] @
Pa napisao sam ti ja gore kako se koristi ta smena. Pogledaj.
[ Sonec @ 09.03.2012. 20:17 ] @
Citat: darkosos: To 7/5 mi nesto sumnjivo... Kad se pomnozi leva strana sa 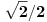 dobija se 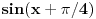 sto tesko moze da se nategne na 7/5...
Da, ali ti onda i 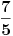 mnozis sa 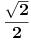 (celu jednacinu, obe strane), pa ces imati 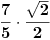 sto je manje od  , pa ne postoji problem. [ darkosos @ 09.03.2012. 20:24 ] @
Stvarno :)
[ cikin @ 09.03.2012. 20:27 ] @
nisam video...uradio sam sad....
[ cikin @ 24.04.2012. 19:57 ] @
odrediti 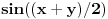 i 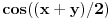 ako je 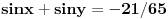 i  ako 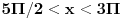 i 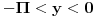 e sad izracunao sam ja sve samo me zanima kako da znam dal je ispred + ili - .... [ Sonec @ 24.04.2012. 20:21 ] @
Pa, dato ti je gde se krecu  i  . Odredi odatle gde se krece 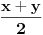 , a na osnovu toga i znak sinusa, odnosno kosinusa. [ darkosos @ 24.04.2012. 20:26 ] @
[ cikin @ 25.04.2012. 17:06 ] @
pogresno sam bio napisao ali shvatio sam,hvala.... jel moze neko ovo da uradi ali da pojasni 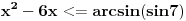 [ Sonec @ 25.04.2012. 20:10 ] @
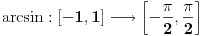
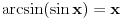 za 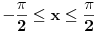
I ostaje ti da 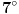 pretvoris u radijane (ako to vec nije u radijanima, a verujem da nije). [ cikin @ 25.04.2012. 23:16 ] @
Sonec ajde uradi ako ti nije tesko, shvatam sta kazes pretvorim u radijane, al kad uradim dobijam razlicito resenje....
[ darkosos @ 26.04.2012. 08:18 ] @
Ako je resenje [-1,7], to znaci da je zeljena interpretacija arcsin(sin 7) = 7 (stepeni), sto ne bi bilo u redu, jer stepene ne mozes da sabiras sa skalarima.
Probaj da interpretiras 7 kao 7 radijana; to je nesto vise od 2pi, pa bi trebalo da je 7-2pi taman izmedju -pi/2 i pi/2.
[Ovu poruku je menjao darkosos dana 26.04.2012. u 09:29 GMT+1]
[ cikin @ 26.04.2012. 13:33 ] @
darkosos po tvom dobijem tacno resenje...a jel 7-2pi od 7 oduzimam samo 2kpi (msm ne mogu da oduzmem pi/2) svodim ga gde je definisan arcsin....
[ darkosos @ 26.04.2012. 13:38 ] @
Pogledaj sta je napisao Sonec, kada je arcsin(sin x)=x. Dakle, kada svedes ugao na taj interval, mozes primeniti ovu jednakost, i to je ono sto sam ja uradio.
Dakle, nije pitanje gde je definisan arcsin, jer sin x ce uvek dati "dobru" vrednost, vec kada vazi navedena jednakost...
EDIT: na x ovde mozes primeniti bilo sta sto nece promeniti vrednost sin, a cijl ti je da uguras x u odgovarajuci interval...
[ cikin @ 28.04.2012. 20:56 ] @
moze neko da pomogne kako samo da zapocnem.... 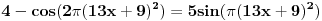 [ darkosos @ 28.04.2012. 21:02 ] @
Mozda ce biti citljivije ako stavis 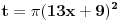 pa bi imao 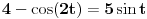 pa bi dalje mogao koristeci formulu za cos dvostrukog ugla. [ cikin @ 08.06.2012. 11:00 ] @
samo neko da mi kaze kako ( ne mora da radi).... 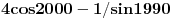 (stepeni) [ Sherlock Holmes @ 08.06.2012. 11:11 ] @
Pretpostavljam da nije jasno sta da radis sa "ovolikim" stepenima. Period sinusa i kosinusa je 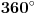 . Na primer : 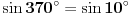 . Mozes pomocu trigonometrijske kruznice to da zakljucis. [ Nedeljko @ 08.06.2012. 11:36 ] @
Prvo, ovo nije jednačina. Kako tačno glasi zadatak?
[ cikin @ 08.06.2012. 20:20 ] @
znam da nije jednacina da ne otvaram novu temu, i znam da radim sa "tolikim stepenima".... pa glasi izracunati vrednost izraza....
[ Nedeljko @ 08.06.2012. 21:23 ] @
Pa, onda napiši dokle si stigao. Za početak skreši stepene. Ne treba valjda i to da računamo?
[ cikin @ 08.06.2012. 22:07 ] @
evo uradio sam... 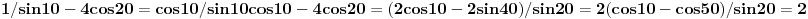 [ selena82seka @ 13.02.2013. 17:11 ] @
Jel može pomoć oko sledećeg zadatka...
arctgx+arctg (1-x)/(1+x)=-3π/4
[ miki069 @ 13.02.2013. 23:30 ] @
Odradi tnagens leve strane jednak tangensu desne strane.
Levo će ti trebati adiciona formula za tg(alfa + beta), a desno imaš 1.
[ selena82seka @ 20.02.2013. 14:02 ] @
Odradeh, ali dobijam 1=1... :(
Tj. dobijam, kad primenim tu formulu : (x^2+1)/(x^2+1)=1
[ miki069 @ 20.02.2013. 15:16 ] @
Baš tako.
Jednačina ima beskonačno mnogo rešenja,
Svako X<>-1.
Samo bi na desnoj strani trebalo da bude pi/4.
Odradi adicionom formulom tangens(pi/4 - X) i sve će ti biti jasno.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|