Jel na faksu ili u gimnaziji?

Nisam još radio realni deo, pa još uvek ne znam.

Misliš



?

je l' ovo Banahova teorema o nepokretnoj tacki?

Očigledno nije. Ima još jedan uslov: .

Je li lakše ako kažem "Korovkinova teorema"?

Da uradim ja zadatak?

Samo rokaj

Zašto ako nikoga ne zanima?

Sacekaj jos koji dan :)

Neka je linearni omotač skupa .

1. Jasno je da tražena relacija važi za sve .

2. Za svaku funkciju , postoji tako da je i .

Zaista, neka je takvo da je i za i . Neka je [/tex]G_n=\{t\in T\,|\,f(t)<g_n(t)[/tex]. Ovo je rastući niz otvorenih skupova čija je unija ceo skup , pa zbog kompaktnosti postoji neko za koje je . Za takvo može se uzeti da je .

3. Za svako i postoji konačno mnogo funkcija takvih da za važi .

Zaista, svakom možemo pridružiti funkciju takvu da je i . Za . Očigledno je ovo familija otvorenih skupova, čija je unija ceo kompakt , pa postoje takvi da je , pa se može uzeti da je .

4. Neka su . Za i postoji takvo da za svako važi .

Neka je i takvo da za i važi . Za je odakle je .

5. Važi traženo tvrđenje.

Dokazaćemo da za svako postoji takvo da za svako važi . Obrnuta nejednakost se dokazuje analogno.

Neka su takve da za važi i neka je takvo da je za . Tada za važi .

Hajde da primenimo ovu teoremu na Bernštajnove polinome.

Bernštajnov operator na prostoru se definiše na sledeći način:

.

Diferenciranjem po jednakosti , a potom i množenjem sa , dobijamo da je

.

Primenom istog postupka na ovu jednakost dobijamo da je

.

Neka je . Primenom prethodnih jednakosti izvodi se da je

, i .

Stoga uniformno konvergira ka na segmentu kada teži beskonačnosti, za sve .

Skup ispunjava tražene uslove zato što obuhvata funkcije oblika .

Za ma koju nenegativnu funkciju i važi

.

Primetimo još da su ovi operatori linearni, tj. za ma koje funkcije i skalare važi .

Stoga uniformno konvergira ka na segmentu kada teži beskonačnosti, za sve .

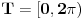
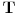
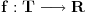
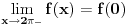
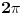
Neka je na poluintervalu definisana metrika sa . U ovoj metrici je skup kompaktan. funkcija je neprekidna u toj metrici domena akko je neprekidna u standardnoj metrici domena i pritom je , pa ovakve funkcije možemo poistovetiti sa -periodičnim funkcijama koje slikaju skup realnih brojeva u njega samog.

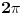
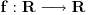
Furijeovi koeficijenti lokalno integrabilne -periodične funkcije se definišu na sledeći način:

, , , ,

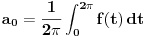
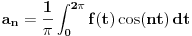
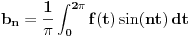
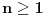
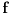
gde se Furijeov red funkcije definisan kao .

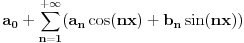
Parcijalna suma ovog reda je

.

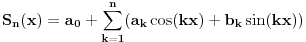
Očigledno je

,

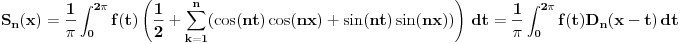
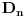
gde je Dirihleovo jezgro definisano sa



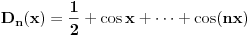
Očigledno je

.

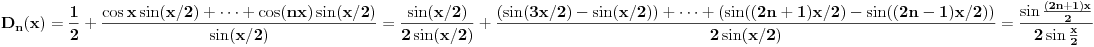
Fejerovo jezgro se definiše kao

.

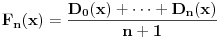
Na sličan način kao malopre se dobija da je

.

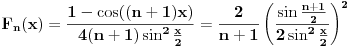
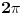
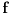
Fejerov operator se definiše kao operator koji lokalno integrabilnoj -periodičnoj funkciji pridružuje funkciju

.

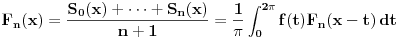
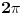
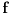
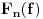
Dokažimo da za neprekidnu -periodičnu funkciju niz uniformno konvergira ka .

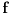
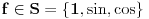
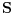
Zahvaljujući pozitivitetu Fejerovog jezgra, Fejerov operator je pozitivan, tako da je dovoljno proveriti ovaj stav u slučaju kada jer skup obuhvata funkcije oblika .

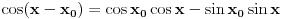
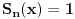
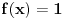
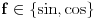
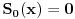
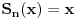
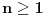
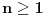
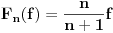
Znajući da je za , odnosno da je za ispunjeno i za , dobijamo da je za ispunjeno za .

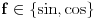
Time je tvrđenje dokazano.