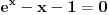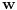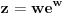Metode za rešavanje jednačina u Mathematici

[ paga @ 06.07.2010. 14:38 ] @

Pozdrav svima

Da li neko zna kako se na engleski prevodi: rešavanje jednačina metodom polovljenja intervala .

Treba u numeričkoj da nađem rešenje sledeće jednačine :

Moram da ga uradim peške i da dostavim rešen zadatak isto polovljenjem intervala u programu mathematica

Peške nije problem a nije ni preko mathematice , samo kad bi neko znao da mi kaže gde da gledam tehničku dokumentaciju za ovu oblast .

[ Cabo @ 06.07.2010. 14:57 ] @

http://www.lmgtfy.com/?q=find+root+interval

[ holononi @ 06.07.2010. 15:01 ] @

The Halving Method
Bisection method

[ paga @ 06.07.2010. 15:01 ] @

Našao sam odgovor na strani http://reference.wolfram.com/m.../NumericalEquationSolving.html

Međutim , ne mogu da dobijem rešenja za ovu gore jednačinu .
Kaže :

[ holononi @ 06.07.2010. 15:10 ] @

Dobio si rešenje. Proveri sa x=0.

[ Cabo @ 06.07.2010. 15:12 ] @

Pa uradi to što ti predlaže:

Code:
Reduce[E^x-x-1==0]

daje

Code:
(C[1] \[Element] Integers && x == -1 - ProductLog[C[1], -(1/E)]) ||
x == 0

Iz Help-a:

Citat:

ProductLog[z] gives the principal solution for

ProductLog[k,z] gives the

-th solution.

[ atomant @ 06.07.2010. 16:04 ] @

Pa napisi funkciju koja ce da ti radi polovljenje intervala. Nemoj da ocekujes da je NSolve svemoguca

Code:
PolovljenjeIntervala[f0_, {x_, a0_, b0_}] := Module[
   {f, a, b, c},
   a = N[a0];
   b = N[b0];
   f = Function[x, f0];
   c = a + 0.5*(b - a);
   While[a < c < b,
    If[Sign[f[c]] == Sign[f[a]],
     a = c, b = c];
    c = a + 0.5*(b - a)];
   c];

Eto, ovo ce ti resiti problem.
Pozivas je na sledeci nacin:

Code:
PolovljenjeIntervala[Exp[x] - x - 1, {x, -1, 1}]

i dobijes

Code:
-1.05367*10^-8

a to je 0 u sustini

Lupio sam ove granice, namerno nisam stavio 0, nego oko nje. Znaci ovo a i b su pocetne tacke. Znas vec i sam, da ti ne pricam mnogo. Naravno, funkciju mozes nazvati kako god hoces.

[ Cabo @ 06.07.2010. 16:17 ] @

Code:
Chop[-1.05367*10^-8, 10^-4]

daje nulu. :o)

[ atomant @ 06.07.2010. 16:21 ] @

-0.0000000105367 je toliko malo da je nula :P

[ paga @ 06.07.2010. 17:34 ] @

Ali problem je u tome što je meni potrebno najmanje pozitivno rešenje .

Faktički nula je jedino rešenje .

Kako da onda nađem pozitivno rešenje (da li ih ima više od jednog?)?

[ atomant @ 06.07.2010. 18:14 ] @

Ta jednacina ima jedno resenje. I to resenje je 0, sto se vidi iz same jednacine, ne mora ni da se resava. Ako hoces, ti reci da ti je 10^(-15) resenje (ako neces 0), recimo. Kad to ubacis dobices neki izraz koji je jako blizu nule i onda ga proglasi za 0. Ali 0 je jedino resenje ove jednacine. Mozes da izvodis bezbroj resenja na ovaj nacin, svako manje od prethodnog, ali ne mozes pobeci od cinjenice da je 0 jedino pravo resenje.

[ Cabo @ 07.07.2010. 10:33 ] @

Matematika je dala i ovo:

Code:
(C[1] \[Element] Integers && x == -1 - ProductLog[C[1], -(1/E)])

To u prevodu na „matematički jezik“ znači ovo: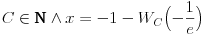

gde je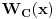

grana Lambertove funkcije koja odgovara parametru

.

Videti i, npr. Lambert W function.

ISPRAVKA: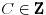

_{[Ovu poruku je menjao Cabo dana 07.07.2010. u 18:31 GMT+1]}

[ paga @ 07.07.2010. 20:41 ] @

Ovo su definitivno najkvalitetniji odgovori .
Uspešno odrađen zadatak , čak sam i čitao o Lambertovoj funkciji i ako nisam matematičar .

Hvala svima i pozdrav do sledeće prilike .