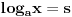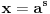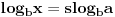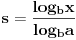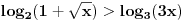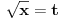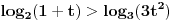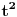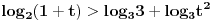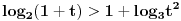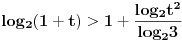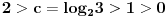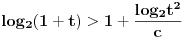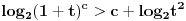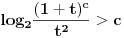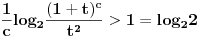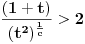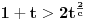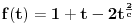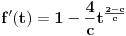[ jovanrisitc @ 09.07.2010. 12:19 ] @
| Molim za pomoc kako da krenem sa resavanjem sledece nejednacine koja se cesto javlja na blanketima. Problem je kako da svedem logaritam na iste osnove, za konkretan primer rec je o logaritmima sa osnovama 2 i 3 respektivno. Nejednacina je: log2(1+ sqrt(x)) > log3(3x) |