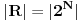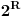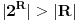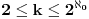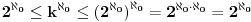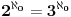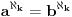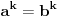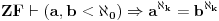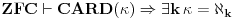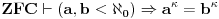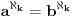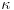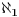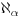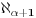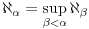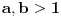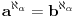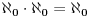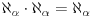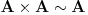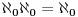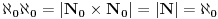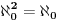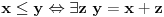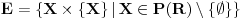[ boxxter @ 14.07.2010. 11:27 ] @
|
| @holononi -Ako pod "neizračunljivosti skupa realnih brojeva" podrazumeš neprebrojivost intervala realnih brojeva tada se može reći da postoji sličnost izmedju konstrukcija i skupa u Raselovom paradokusu. Možete pogledati na primer http://wapedia.mobi/en/Cantor%27s_diagonal_argument.
Nisam rekao da postoji slicnost, nego da su iste vrste. I postoji dokaz koji jasno i nedvosmisleno ukazuje na to.
Citat: Sini82:
Nemoj učiti matematiku sa wikipedie. Nisi dobro preveo tekst, vjerovatno ga nisi dobro ni shvatio. Ne radi se o neizračunjivosti nego o neprebrojivosti skupa realnih brojeva. Nije Kantorov dijagonalni argument, nego Kantorov dijagonalni postupak.
Evo ga, stigao je novi Ajnstajn. Ajde molim te dokazi mi ovde da je pogresno da koristim izraz " dijagonalni argument". Bas bih voleo da cujem zasto i kako je to pogresno. Oba izraza koristim namerno. |
[ boxxter @ 14.07.2010. 11:53 ] @
Da koristite izraz- neizracunjljivost, i argument, bilo bi vam jasnije :D.
Neka je R = [0, 1] i N je skup pozitivnih celih brojeva. Ako razmisljamo o realnim brojevima predstavljenim binarnom izrazom, onda uz neke nedostatke, svaka od tih ekspanzija je karakteristicna funkcija, podskupa N, koje se pridruzuje za svako x ∈ R podskupa N, podskupa indeksa, ciji odgovarajuci znakovi u binarnom izrazu od x su 1. Takva asocijacija govori da je 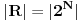 . I nuznost 2. govori da je |R| > |N|.
Jasno je da su "neprebrojivost" skupa realnih brojeva, i Raselov paradoks, iste vrste.
Dijagonalni argument
Nuznost 2
Za svaki skup R , kardinalnost 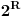 je striktno veca, nego kardinalnost od R.
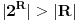 [ Nedeljko @ 14.07.2010. 12:01 ] @
Alo, izračunljivost je nešto sasvim drugo od prebrojivosti. [ Nedeljko @ 14.07.2010. 12:02 ] @
No, sve to i dalje nema veze sa aksiomom regularnosti iz teorije skupova.
[ boxxter @ 14.07.2010. 12:07 ] @
[ Nedeljko @ 14.07.2010. 12:17 ] @
Naravno da tebi pored svog pokazanog neznanja nije jasna razlika između babe i žabe.
[ Sini82 @ 14.07.2010. 12:19 ] @
boxxter:
Code:
Evo ga, stigao je novi Ajnstajn. Ajde molim te dokazi mi ovde da je pogresno da koristim izraz
" dijagonalni argument". Bas bih voleo da cujem zasto i kako je to pogresno. Oba izraza koristim
namerno.
Molim te, poštedi me sarkazma. Pravilnije je reći Google: "kantorov dijagonalni postupak" ili
kada već prevodiš "argument dijagonalizacijom". Nigdje ti nisam napisao da je pogrešno, možeš ga zvati
što se mene tiče i "dijagonalni deterdžent". Naziv je stvar dogovora ali mora tačno da se definiše šta taj
naziv označava, što baš tebi i ne polazi za rukom.
[Ovu poruku je menjao Sini82 dana 14.07.2010. u 13:30 GMT+1]
[ Picsel @ 14.07.2010. 12:35 ] @
Izvinjavam se sto upadam u raspravu, ali citam http://en.wikipedia.org/wiki/Cardinality_of_the_continuum. Nisam matematicar pa mi nije bas sve najjasnije. Moze li neko da mi objasni zasto je |R|=2^alef? Zasto ne, recimo, 3^alef? Po ovom intuitivnom argumentu na wiki stranici, posmatra se binarna baza. Zasto bas binarna, zar ne bi resenje bilo 8^alef ako bi posmatrali oktalnu bazu?
[ Nedeljko @ 14.07.2010. 12:40 ] @
Neka je 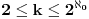 . Tada je 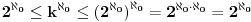 .
Izaberi koju god hoćeš osnovu, dobićeš isti rezultat. [ boxxter @ 14.07.2010. 12:41 ] @
Citat: Sini82: boxxter: Nigdje ti nisam napisao da je pogrešno
Pa ako nisi pokazao da je pogresno, ne znam oko cega se raspravljamo. :S
Citat: Nedeljko: Naravno da tebi pored svog pokazanog neznanja nije jasna razlika između babe i žabe.
Steta. Bas si bio blizu da povezes te dve stvari, i karakteristicne funkcije, topolosku ekvivalentnost. Mozda bi dosao do neke harmonije. Ali ti zbog svoje pokazane ogranicenosti, nisi sposoban da vidis relacije. Odmoricu malo. Usko je ovde, i mracno. I dosadno je. Ne znam ko je kriv za to. Fantasticna ogranicenost.
[ Nedeljko @ 14.07.2010. 12:44 ] @
Picsel
Konkretno, 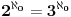 . [ Picsel @ 14.07.2010. 12:48 ] @
Da, svakako. Ne znam kako sam to prevideo...
Hvala
[ holononi @ 14.07.2010. 14:13 ] @
Uz pretpostavku aksioma izbora za a,b > 1, a,b konačni važi 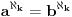 . [ Nedeljko @ 14.07.2010. 14:25 ] @
1. Tako kako si napisao, aksioma izbor nije potrebna - dokazivo je u ZF. Da si napisao 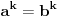 za ma koji beskonačan kardinal  , onda bi bila potrebna. Ako se ograničiš samo na alefe (koji su inače po aksiomi izbora jedini kardinali), onda ne treba.
2. Aksioma je jedna od standardnih aksioma teorije skupova. Čemu isticanje svake njene primene? Zašto se ne ističe onda i primjena ostalih aksioma.
Ovako se stiče lažan utisak da u matematici postoji jedna aksioma i da se teoreme dele na one koje slede iz nje i one koje slede niizčega, što svakako nije tačno. [ holononi @ 14.07.2010. 14:39 ] @
U (1) si prihvatio aksiom izbora pa ostalo neću ni da čitam.
[ Sini82 @ 14.07.2010. 15:42 ] @
boxxter:
Code:
Pa ako nisi pokazao da je pogresno, ne znam oko cega se raspravljamo. :S
Nije mi bila namjera da se raspravljamo, nego da ti olakšam google pretragu, da lakše pronađeš ono što te interesuje.
Pogledaj i ovdje: Google: "argument dijagonalizacijom".
[ Nedeljko @ 14.07.2010. 15:51 ] @
Citat: holononi: U (1) si prihvatio aksiom izbora pa ostalo neću ni da čitam.
Gde?
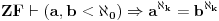 .
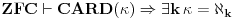 .
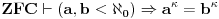 .
Lepo piše šta iz čega sledi. [ Nedeljko @ 14.07.2010. 16:17 ] @
Pogledao sam. Velja Abramović je sjajan po svom običaju, ali nije za ovaj forum, već za Ultra MadZone.
[ holononi @ 14.07.2010. 17:41 ] @
Ponoviću šta si napisao
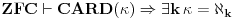 .
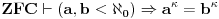 .
Pa ne vidim šta se to razlikuje od onog što sam ja napisao 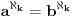 , uz dodatnu pretpostavku a,b > 1. Jedino što si ti "elegantno" u eksponent stavio "kapa" umesto "aleph_k". Medjutim iz tvog komentara sledi a,b >= 0, što nije moja pretpostavka.
Ono prvo
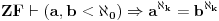
važi ako se skup može urediti. U ZFC se svaki skup može dobro urediti pa u ZFC svaki skup ima kardinalnost. U ZF se ne može govoriti o kardinalnosti svakog skupa. [ Nedeljko @ 14.07.2010. 18:11 ] @
Alefi jesu dobro uređeni već u ZF. U ZF se bekonačan skup može dobro urediti akko ima alef. Stoga ono što si napisao važi u ZF.
E, sad, ako napišeš 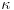 , tu nigde ne piše da taj kardinal ima alef.
Razvijeniji zapis tog opštijeg tvrđenja je
Ako skupovi A i B imaju po bar dva elementa i konačni su i ako je skup C beskonačan, onda je skup preslikavanja skupa C u skup A ekvipotentan sa skupom svih preslikavanja skupa C u skup B.
Skup je konačan ako je svako injektivno preslikavanje njega u njega samog ujedno i surjektivno.
Da, ovo opštije tvrđenje nije teorema ZF, ali tvoj specijalan slučaj za skupove koji imaju alef svakako jeste. [ Nedeljko @ 14.07.2010. 18:13 ] @
Citat: holononi: Medjutim iz tvog komentara sledi a,b >= 0, što nije moja pretpostavka.
Kardinali ne mogu biti negativni. [ holononi @ 14.07.2010. 18:53 ] @
Aj sad da pišemo po jedan komentar za svaku rečenicu da bi se popeli na vrh liste matematika.
Da li bi hteo da se držiš onoga što sam napisao. Uvodiš gomilu "akosa" i pripisuješ ih meni. Na svaki stav tako možeš prikačiti da je suprotan sam sebi. Ne znam koja svrha.
U ZF se samo zna da izmedju  i 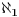 nema drugih kardinalnih brojeva a o punom bogatsvu uredjenja kardinalnih brojeva ćemo govoriti tek po uvodjenju aksioma izbora.
Naravno, očekujem da se ovaj stav tebi ne dopada.
Ovo si dobro primetio. Ko je napisao takvu glupost ? [ boxxter @ 14.07.2010. 18:57 ] @
Citat: Sini82: boxxter:
Code:
Pa ako nisi pokazao da je pogresno, ne znam oko cega se raspravljamo. :S
Nije mi bila namjera da se raspravljamo, nego da ti olakšam google pretragu, da lakše pronađeš ono što te interesuje.
Pogledaj i ovdje: Google: "argument dijagonalizacijom".
Nije ni meni namera da se raspravljamo. Izvinjavam se sto sam ponekad tesko razumljiv. Rekao sam da sam oba izraza upotrebio namerno. I svi ovi dokazi trebali su da vode ka jos inspirativnijem razgovoru. Puno vremena provodim u prevodu integralnih tekstova nekih pojmova. Vama je to verovatno beznacajno i besmisleno. Ime stvari za mene ima poseban znacaj. Sustinski. Priznajem da imam ekscentrican smisao za humor, izgleda samo meni razumljiv. Probacu da ispravim to. Ako mogu. [ Sini82 @ 14.07.2010. 19:34 ] @
Ako budeš imao problema otvori posebnu temu da ti pomognemo u prevodu (naravno ne kompletnih tekstova, iako nije loše da postaviš link prema potpunom tekstu) koliko možemo.
[ Nedeljko @ 14.07.2010. 20:57 ] @
Citat: holononi: Da li bi hteo da se držiš onoga što sam napisao. Uvodiš gomilu "akosa" i pripisuješ ih meni. Na svaki stav tako možeš prikačiti da je suprotan sam sebi. Ne znam koja svrha.
U ZF se samo zna da izmedju  i 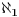 nema drugih kardinalnih brojeva a o punom bogatsvu uredjenja kardinalnih brojeva ćemo govoriti tek po uvodjenju aksioma izbora.
Ne znam šta su akosi, ali ovo što si napisao jednostavno nije tačno. U ZF svakom dobrom uređenju odgovara ordinal  i svakom ordinalu  odgovara alef 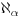 . Pritom je  najmanji beskonačan kardinal, 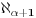 najmanji kardinal veći od 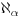 (koji postoji po Hartogsovoj teoremi), a za granični ordinal  je 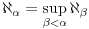 .
Citat: holononi: Ovo si dobro primetio. Ko je napisao takvu glupost ? Citat: holononi: Medjutim iz tvog komentara sledi a,b >= 0, što nije moja pretpostavka. [ holononi @ 14.07.2010. 22:34 ] @
Kad već citiraš nemoj izvlačiti iz konteksta. U tom tekstu piše:
Pa tu ne stoji (niti se može izvući zaključak) da je reč o negativnim brojevima. Ako si ti izvukao takav zaključak trebalo bi da se zamisliš.
I ne vidim čemu teatralni supremumi kad si i sam već potvrdio to što sam napisao jedino što si propustio da dodaš a,b > 1, a,b konačni.
[ Nedeljko @ 14.07.2010. 23:17 ] @
Ovo nije tačno
Citat: holononi: U ZF se samo zna da izmedju  i 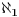 nema drugih kardinalnih brojeva a o punom bogatsvu uredjenja kardinalnih brojeva ćemo govoriti tek po uvodjenju aksioma izbora. [ holononi @ 14.07.2010. 23:27 ] @
Dobro po tebi nije tačno, po nekima koji znaju više i od mene i od tebe zajedno jeste tačno.
I šta sad ?
[ Nedeljko @ 14.07.2010. 23:37 ] @
Po kojima to, leba ti?
[ holononi @ 14.07.2010. 23:42 ] @
Da ti nisi možda Ljutko ?
Razbacao si se dokazujući kako nije tačno ono što sam ja napisao a ti si sam to isto napisao.
Priklješten, sad menjaš metu. Nije loše. Tako love iskusni lavovi.
[ Nedeljko @ 14.07.2010. 23:49 ] @
Po tebi ispade da ne postoje ni 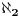 ni 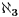 u ZF. Jesam li ja to napisao? O čemu ti pričaš? U ZF imaš koliko god hoćeš alefa. Postoji prirodna bijekcija između ordinala i alefa već u ZF. To što ti ne razumeš ni knjige koje čitaš, ni moje postove je apsolutno tvoj problem. [ holononi @ 15.07.2010. 00:16 ] @
Da to si ti napisao. U tom mom komentaru ne stoji da "ne postoje 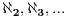 " i to baš u ZF, već stoji da izmedju kardinala  i i 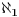 nema drugih nema drugih kardinala, pa ti se zahvaljujem na korektnom citatu u pretposlednjem postu ali to što izvodiš proizvoljne zaključke nije moj problem.
Štaviše, pretpostavio sam da ti se taj stav neće dopasti ( http://www.elitesecurity.org/t247222-3#2648653). Kao da čitam misli. [ Nedeljko @ 15.07.2010. 00:30 ] @
Gde sam ja to napisao? Ovo je već nepošteno!
Napisao si da se u ZF zna samo da između  i 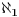 nema drugih kardinala, a bogatsktvo uređenja kardinala da dobijamo tek sa aksiomom izbora.
No, vrati se na ono od čega se pošlo.
Za konačne 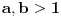 je 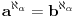 već u ZF. Ko li ovde menja metu? [ holononi @ 15.07.2010. 18:46 ] @
Dokazati 2Aleph_0 je kardinal.
[ Nedeljko @ 15.07.2010. 21:49 ] @
Ako koristiš definiciju kardinala kao alefa, onda:
1. U ZF ne može.
2. U ZFC je trivijalno.
[ holononi @ 16.07.2010. 18:57 ] @
[ Nedeljko @ 16.07.2010. 19:33 ] @
[ holononi @ 16.07.2010. 22:02 ] @
Multiplikativna aksioma.
[ Nedeljko @ 16.07.2010. 22:13 ] @
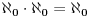 se dokazuje elementarno u ZF.
Takođe, u ZF za ma koji ordinal  važi 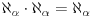 .
Aksioma izbora je potrebna da bi dokazao da za ma koji beskonačan skup  važi 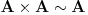 .
U ZF to važi za skupove koji se mogu dobro urediti, tj. koji imaju alef. [ holononi @ 17.07.2010. 05:05 ] @
Nemojmo sada skretati metu na umotvorine.
Zermelova teorema o dobrom uredjenju povlači AC.
[ Nedeljko @ 17.07.2010. 10:34 ] @
Očigledno brkaš dve stvari:
1. Svi skupovi se mogu dobro urediti.
2. Neki skupovi se mogu dobro urediti.
1 važi u ZFC, a 2 već u ZF. Ja nigde nisam koristio činjenicu da se svi skupovi mogu dobro urediti, ali oni koji imaju alef, mogu u ZF.
[ holononi @ 17.07.2010. 15:41 ] @
Opet si počeo da se baviš ličnostima i brkovima.
[ Nedeljko @ 17.07.2010. 22:48 ] @
Kojim ličnostima? Za mene neko ko nema ime nije ličnost.
U nedostatku argumenata, davljenik se za slamku shvata.
[ holononi @ 18.07.2010. 09:41 ] @
Na ovaj tvoj komentar primetiću samo da čovek treba biti nekulturan da bi tako nešto pisao.
Školski dokaz 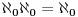 :
Neka je N 0 = N U {0} i F: N -> N 0 dato sa F(n) = n - 1, n element N. F je bijekcija i važi |N 0| = |N| =  .
Lema: Svaki broj n element N se može na jedinstven način prikazati u obliku:
n = 2 r(2s + 1), r, s element N 0. Označimo ovaj prikaz sa (*)
Postojanje prikaza se dokazuje indukcijom po n. Takodje se jedinstvenost lako dokazuje.
Definišemo preslikavanje f: N 0 x N 0 -> N sa
f((r,s)) = 2 r(2s + 1)
f je injekcija jer je prikaz (*) jedinstven. Da je f na sledi iz postojanja istog prikaza. Zato je f bijekcija odakle:
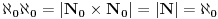
Ništa bez starog dobrog aksioma izbora. [ Nedeljko @ 18.07.2010. 11:09 ] @
I gde je tu aksioma izbora?
[ holononi @ 18.07.2010. 11:20 ] @
Funkcija izbora ako i samo ako aksioma izbora.
[ Nedeljko @ 18.07.2010. 12:16 ] @
U kom konkretno koraku tvrdiš da si je upotrebio?
[ holononi @ 18.07.2010. 13:23 ] @
U drugoj jednakosti poslednjeg izvodnjenja. Mora se dokazati ekvipotentnost tih skupova.
[ Nedeljko @ 18.07.2010. 14:00 ] @
Čeka, a čemu ti onda služi celo ono izvođenje ako tu ekvipotentnost treba ponovo da dokazuješ?
[ holononi @ 18.07.2010. 15:57 ] @
Ti se u svom dokazu pozivaš na multiplikativnu aksiomu (ekvivalent AC) ( http://www.elitesecurity.org/t405228-0#2648386)
Ja sam samo pokazao da postoji funkcija izbora pa opet AC. [ Nedeljko @ 18.07.2010. 16:23 ] @
Ne, ja sam koristio TEOREMU ZF teorije da je 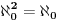 .
Sam si izveo tu jednakost sredstvima ZF, tako da nema potrebe da i ja navodim dokaz. Gde misliš da je u onom izvođenju korišćena AC?
Razumeš li o čemu pričam? Prvo si dokazao ekvipotentnost N x N i N, a onda na kraju tražiš da se opet dokazuje. Gde misliš da je AC u onom dokazu ekvipotentnosti? [ Nedeljko @ 18.07.2010. 16:29 ] @
Multiplikativna teorema tvrdi da u opštem slučaju, dakle za ma koji beskonačan skup A, važi da je A ekvipotentno sa A x A.
To tvrđenje je u nekim specijalnim slučajevima dokazivo sredstvima ZF.
Na primer, u ZF to tvrđenje važi za svaki beskonačan skup koji se može dobro urediti, tj. koji ima alef, a takođe za svaki sku A postoji njegov beskonačan nadskup B takav da je B x B ekvipotentno sa B. Toliko je dokazivo u ZF.
[ holononi @ 18.07.2010. 17:18 ] @
Ti konstruišeš kule u oblacima. Neko će pomisliti da ja negiram kompletnu teoriju skupova. Iz toga što kažem da je 1+1 veće od jedan ne sledi da sam tvrdio da je veće od 5 kako otprilike izgledaju tvoji komentari i dokazi. Kao da niko osim tebe nije čuo za direktan proizvod. Ja ne galamim toliko pa sam samo diskretno napomenuo da je AC ekvivalent multiplikativnoj aksiomi. Iz toga si već trebao izvući zaključak da nema potrebe da objašnjavaš to što objašnjavaš jer neko će pomisliti da to nisu ekvivalentna tvrdjenja.
Dokaz koji sam naveo je ispravan (nije moj, možeš čuti na predavanjima). No kako je čovek konstruisao funkciju izbora izvukao sam zaključak da važi AC (opet ni taj stav nije moja umotvorina, dokaz imaš u literaturi). Možeš pobijati moj zaključak ali ne možeš tvrditi da ja tvrdim nešto što ne tvrdim.
[ Cabo @ 18.07.2010. 18:40 ] @
Ovaj, jel ovo još jedna od „onih“ tema u kojima neka reinkarnacija Tesle „ruši“ matematiku?
-______________________-
[ holononi @ 18.07.2010. 18:57 ] @
Ako imaš dokaz bez funkcije izbora slobodno ruši.
[ Nedeljko @ 18.07.2010. 19:35 ] @
1. Gde si u onom dokazu našao izbornu funkciju?
2. AC nije nekakva dozvola za konstrukciju izborne funkcije, već postuliranje njenog postojanja u opštem slučaju, dakle, čak i onda kada ne možeš da je konstruišeš.
[ holononi @ 18.07.2010. 22:16 ] @
Da li je moguće koristiti relaciju prirodnog uredjenja
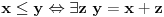
na direktnom proizvodu skupova prirodnih brojeva ? [ Nedeljko @ 18.07.2010. 22:18 ] @
Misliš da su x,y i z uređeni parovi prirodnih brojeva?
[ holononi @ 18.07.2010. 22:40 ] @
Da si napisao "moguće je dokazati bez eksplicitnog pozivanja na AC" bilo bi ispravno jer zaista je moguć takav dokaz. Ti si napisao "važi u ZF" (i to čini mi se više puta). Ali taj dokaz implicira AC pa je tačno "važi u ZFC". To što ti izvrdavaš ne možeš izvrdati jer na direktnom proizvodu ne pomaže prirodno uredjenje.
[ Nedeljko @ 18.07.2010. 23:00 ] @
Koji bre dokaz implicira AC? O čemu ti pričaš?
Na N x N postoji dobro uređenje, npr. leksikografski poredak.
Čovek te lepo pita gde ti je u onom dokazu AC, a ti stalno nešto vrdaš.
[ holononi @ 19.07.2010. 01:24 ] @
Misliš na Zermelovu teoremu o dobrom uredjenju ? Pa to ti je ekvivalent AC.
[ Nedeljko @ 19.07.2010. 01:35 ] @
Gde ti je Cermelo u onom dokazu?
[ holononi @ 19.07.2010. 09:21 ] @
Pre nego što nadmeno počnu da sole pamet drugima pojedinci treba da razmisle o svojim tvrdjenjima.
Tvrdjenje da je nešto tačno pozivanjem na AC nije pogrešno jer to zaista važi uz AC. AC nije kuvar koji kaže kako treba da izgleda funkcija izbora, samo kaže da postoji.
Medjutim, tvrditi da nešto važi bez AC i usput se sapleti o AC je pogrešno.
Prirodno uredjenje ne funkcioniše na skupu NxN pa je dozvoljeno pozvati se na AC i ne mora se eksplicitno tražiti funkcija izbora bez obzira da li ta funkcija postoji. U tom smislu nema ograničenja u AC. U samom AC nije definisano pravilo na kojim skupovima se primenjuje a na kojim ne. Zato se AC može primeniti na sve skupove na kojima prirodno uredjenje ne funkcioniše.
Inače, dokaz koji sam naveo je iz udžbenika jednog od ovdašnjih fakulteta pa nije jasno koja budala je pomislila da je to sa Wikipedia.
[ Nedeljko @ 19.07.2010. 09:28 ] @
Ponavljam pitanje gde je u ONOM dokazu Cermelo ili bilo šta za šta je neophodna AC? Samo nešto vrdaš, a nikako da odgovoriš na jednostavno pitanje, za koji ti korak treba Cermelo ili šta god za šta je neophodna AC.
[ holononi @ 19.07.2010. 09:46 ] @
Ti si se pozvao na dobro uredjenje pa odgovori sam sebi. Ja na to dodajem da ako se skup može dobro urediti to povlači AC (i obratno). To što neko žmuri kad se spotakne o AC nije moj problem.
[ Nedeljko @ 19.07.2010. 09:56 ] @
Ja nisam naveo onaj dokaz, nego ti.
Jasno. Kad te čovek pita nešto sasvim konkretno, ti palamudiš, jer ne znaš da odgovoriš.
Odavde mogu samo da zaključim da ne znaš gde se u onom dokazu koristi AC. Naravno, ne koristi se nigde, ali ti je muka da priznaš da nešto ne znaš.
[ holononi @ 19.07.2010. 10:22 ] @
Nisi definisao "palamudi" pa bi neko mogao pomisliti da padaš u vatru.
Već sam nekoliko puta napomenuo ako imaš funkciju izbora onda to povlači AC. Zato ti ne znaš da li to važi u ZF bez AC. Ali "može se dokazati bez eksplicitnog pozivanja na AC" što je trebalo da bude tvoje tvrdjenje. Medjutim kao i sada tako i onda ti znaš samo za lupanje šakom o sto.
Pretpostavka AC ne čini štetu, ali može pomoći. Ako bi odbacili AC onda je možda potrebno odbaciti mnoga tvrdjenja koja su danas prihvaćena kao važeća.
[ Nedeljko @ 19.07.2010. 10:30 ] @
Znači ne znaš da odgovoriš na jednostavno i konkretno pitanje
Citat: Nedeljko: Za koji korak ONOG dokaza ti treba Cermelo ili šta god za šta je neophodna AC.
Ili treba da ga preformulišem?
Koji korak ONOG dokaza ne prolazi u ZF?
Znaš samo da izvrdavaš. [ holononi @ 19.07.2010. 11:07 ] @
Citat: holononi: http://www.elitesecurity.org/t405228-3#2651590
Već sam nekoliko puta napomenuo ako imaš funkciju izbora onda to povlači AC. Zato ti ne znaš da li to važi u ZF bez AC. Ali "može se dokazati bez eksplicitnog pozivanja na AC" što je trebalo da bude tvoje tvrdjenje.
Trebaš paziti kako formulišeš tvrdjenje da ne pobijaš tvrdjenje koje je tačno. [ holononi @ 19.07.2010. 11:09 ] @
Inače ovakve rasprave su već vodjene i poznate su iz literarture. Ja samo povlačim poteze davno odigrane partije šaha u kojoj ne gubim a dobijam jer ne moram da pobedim.
[ Nedeljko @ 19.07.2010. 11:15 ] @
OK, uporno i tvrdoglavo izvrdavaš. Naravno da ne znaš TS kad ne znaš ni kvantore. Sa tobom je besmisleno raspravljati. Ajd, zdravo.
[ peksimit @ 19.07.2010. 11:16 ] @
Nedeljko, zasto si nervozan? Imaj malo razumevanja...
[ Nedeljko @ 19.07.2010. 11:54 ] @
Deset puta postavljam jedno te isto prosto i konkretno pitanje i on neće ni da kaže "ne znam" ni da odgovori na njega, nego vrda i filozofira. Ne znam šta tu zaslužuje razumevanje.
Sa druge strane, iz ovog njegovog stava
Citat: holononi: ako se skup može dobro urediti to povlači AC
kao i načina na koji ga primenjuje
Citat: holononi: kako je čovek konstruisao funkciju izbora izvukao sam zaključak da važi AC
sledi da ne zna kvanore. [ peksimit @ 19.07.2010. 11:59 ] @
a otkud znamo da ti to znas, a da ne citas i ne prepisujes odnekud i nama prodajes tudje znanje?
[ Nedeljko @ 19.07.2010. 12:04 ] @
To je irelevantno i neutvrdivo on lajn, nevezano sa ovim slučajem.
Ja nisam izmislio TS, ali ne pišem gluposti kao on, tipa "Ako se skup N x N može dobro urediti, onda važi AC".
[ Nedeljko @ 19.07.2010. 12:06 ] @
I još nešto, ja se ne stidim da se sa svojim stavovima potpišem punim imenom i prezimenom, dok se on krije iza kojekakvih pseudonima.
[ peksimit @ 19.07.2010. 12:09 ] @
Nedeljko, izvini, moram da te pitam. Cime se ti bavis u zivotu, premda si konstantno online?
[ Nedeljko @ 19.07.2010. 12:45 ] @
Odgovoreno na PP.
[ peksimit @ 19.07.2010. 13:07 ] @
Ne znam kome, jer meni nista nije stiglo...
[ Nedeljko @ 19.07.2010. 13:29 ] @
U vrhu stranice ispod "Logout" treba da ti je crveno dugme "Provatne poruke".
[ Nedeljko @ 19.07.2010. 15:05 ] @
Je li stiglo?
[ holononi @ 19.07.2010. 17:32 ] @
Dakle kad znaš kvantore onda iznosiš tvrdjenja koja ne možeš braniti.
[ Nedeljko @ 19.07.2010. 17:56 ] @
Ja sam još luđi, što se uopšte raspravljam sa takvim likovima kao što si ti. Elem si nesposoban da razlikuješ opšte od pojedinačnog, elem na svako konkretno pitanje samo izvrdavaš odgovor i palamudiš do u beskonačnost.
[ holononi @ 19.07.2010. 18:25 ] @
Citat: Nedeljko:
"Ako se skup N x N može dobro urediti, onda važi AC"
Izmišljaš, to nisam napisao.
To što ti nisi umeo pravilno da formulišaš svoje tvrdjenje je tvoj problem. Ovde ( http://www.elitesecurity.org/t405228-3#2651590)
Citat: može se dokazati bez eksplicitnog pozivanja na AC
sam te posavetovao kako si trebao formulisati tvrdjenje. Možda postoje i druge formulacije koje ne mogu da se spore ali je i jedna dovoljno.
Tvrdjenje koje sam ja izneo je TAČNO. Tvoje tvrdjenje je takvo da uvek ostavlja sumnju na AC. Kako sam već rekao, ovo je stara rasprava i da si malo čitao o raspravama koje su vodili oni koje ti prezireš kao matematičare verovatno ne bi bilo ni ovolike diskusije.
Naravoučenije: ko iz istorije ne uči moraće da je ponavlja. [ Nedeljko @ 19.07.2010. 22:00 ] @
Citat: holononi: Izmišljaš, to nisam napisao.
Napisao si još veći biser: "ako se skup može dobro urediti, onda važi AC". Znači, nije bitno koji skup, pa može i N x N.
Citat: holononi: Tvoje tvrdjenje je takvo da uvek ostavlja sumnju na AC.
Kako kome. Posle kilometarskih izvrdavanja, ovde si priznao da nisi siguran da li se AC tu koristi ili ne. To si mogao odmah da napišeš. [ holononi @ 20.07.2010. 04:44 ] @
Izvlačiš iz konteksta. I opet lažno citiraš. Nisam napisao da nisam siguran.
Siguran sam da kad da kad dokažeš neki stav onda važi i njemu ekvivalentan stav.
Siguran sam da kad se pozoveš na neki stav onda povlačiš i njemu ekvivalentan stav.
Pa ako važi ekvivalentan stav tada si mogao da ga koristiš bez obzira što tvrdiš "časna reč nisam". Bitno je da si mogao jer je taj stav impiciran nekom fazom u izvodjenju dokaza i zato kažem "ostavlja sumnju".
Ja sam se pozvao na poznata tvrdjenja, pa je na tebi je da dokažeš da funkcija izbora i AC nisu ekvivalenti, na tebi je da dokažeš da dobro uredjenje i AC nisu ekvivalenti pa ću ti poverovati.
Inače to što sam ja napisao ti si potvrdio samo pokušavaš da kažeš da je jedino tako kako ti kažeš.
[ berazorica @ 20.07.2010. 08:22 ] @
Bojan mora da je na pravom odmoru kad ne pomaže raspletu AC zavrzlame!
[ peksimit @ 20.07.2010. 09:02 ] @
@Nedeljko
ja sam ti i odgovorio, ali ne znam da li si primio odgovor?
[ Nedeljko @ 20.07.2010. 09:17 ] @
Citat: holononi: Izvlačiš iz konteksta. I opet lažno citiraš. Nisam napisao da nisam siguran.
Nije nego. Sumnja se u nešto u šta nisi siguran.
Citat: holononi: Siguran sam da kad da kad dokažeš neki stav onda važi i njemu ekvivalentan stav.
Siguran sam da kad se pozoveš na neki stav onda povlačiš i njemu ekvivalentan stav.
Pa ako važi ekvivalentan stav tada si mogao da ga koristiš bez obzira što tvrdiš "časna reč nisam". Bitno je da si mogao jer je taj stav impiciran nekom fazom u izvodjenju dokaza i zato kažem "ostavlja sumnju".
Tačno. Ali nisi siguran da li se tamo koristi neki od ekvivalenata ili ne.
Citat: holononi: Ja sam se pozvao na poznata tvrdjenja, pa je na tebi je da dokažeš da funkcija izbora i AC nisu ekvivalenti, na tebi je da dokažeš da dobro uredjenje i AC nisu ekvivalenti pa ću ti poverovati.
Odavde se vidi da nisi u stanju da razlikuješ opšte od pojedinačnog. Takvima ne vredi ništa dokazivati. [ Nedeljko @ 20.07.2010. 09:19 ] @
Citat: peksimit: @Nedeljko
ja sam ti i odgovorio, ali ne znam da li si primio odgovor?
Nisam još. Izgleda da ES sistem privatnih poruka ne funkcioniše najbolje. [ peksimit @ 20.07.2010. 10:15 ] @
Ne znam da li ti je stigla poruka ili ne, ali je sustina da to sto imas net na poslu ne znaci da vreme treba da provodis ćaskajući po forumima. Te stvari se rade mimo radnog vremena. Time pokazuješ poštovanje prema poslodavcu, a i ističeš svoje radne navike. Ono što ja mogu da zaključim je da si se ti celokupno fokusirao na ono što ćeš da napišeš ovde. Razmisli malo o tome!
[ Nedeljko @ 20.07.2010. 10:21 ] @
Ne, nisam se fokusirao na ovo. Ovo odlepim uzgred, a fajerfoks je upaljen u pozadini sa raznim tabovima koji mi trebaju i + ES-om, pa zato izgleda da non stop visim ovde.
[ peksimit @ 20.07.2010. 10:27 ] @
U svakom slucaju ovo su privatni razgovori i ne bi trebali da se vode za vreme radnog vremena. Ti ostavljas gomilu postova, a sve ti to odvlaci vreme.
Pretpostavljam da radis od 10h, jer tada krenes da saljes postove. Premda ti je danasnji post postavljen u 10:17 ili ti izdvojiš prvih 17 minuta za obavljanje službenih stvari ili još gore, kasnio si na posao i odmah si seo na forum.
Razmisli malo o svom pristupu i da li si efektivan, da ne kažem rentabilan?
[ holononi @ 20.07.2010. 10:38 ] @
Neki stvarno imaju problem pri razlikovanju opšteg od pojedinačnog.
Evo formulacije aksiome izbora:
Citat: Za familuju E skupova, koji nisu prazni (mogu imati zajedničkih elemenata) postoji uvek jedno preslikavanje (korespondencija) po kome svakom elementu S, familije E odgovara jedan element f(S) od S.
Dakle, na konkretnoj familiji skupova, samo se kaže da POSTOJI, nema drugih uslova, nema pravila kako treba da izgleda, da li može da se odredi ili ne i slično. Ako u konkretnom primeru eksplicitno odredite funkciju izbora tada ste implicirali AC. Kad na konkretnom primeru odredite funkciju izbora to važi samo za taj primer i ne mora da važi za bilo koji drugi (takva obavza ne postoji u formulaciji AC).
[ Nedeljko @ 20.07.2010. 10:43 ] @
Preciznija formulacija je:
Za SVAKU familiju E nepraznih skupova postoji funkcija f sa domenom E za koju važi da je f(x) element od x za ma koje x iz E.
I ne reče gde je AC u ONOM dokazu.
[ Nedeljko @ 20.07.2010. 10:43 ] @
@peksimit
Hvala, mama!
[ peksimit @ 20.07.2010. 10:55 ] @
To kako si ti to napisao ima značenje da si ti mama, pošto si stavio zapetu.
Svakako, ja nisam tvoja mama, ali ti ime Đorđe možda nešto znači?
[ holononi @ 20.07.2010. 11:04 ] @
@Nedeljko
Shvatili smo, ti si najveći.
Ali eto, nedelju dana bezuspešno se upinješ iz petnih žila da izadješ na kraj sa jednim oblikom Raselovog paradoksa.
[ Nedeljko @ 20.07.2010. 21:31 ] @
I vrapcima je jasno da nećeš odgovoriti na konkretno pitanje, koliko god puta da se postavi, a i razlozi su očigledni, pa više nema potrebe da se javljaš.
[ holononi @ 21.07.2010. 05:36 ] @
Nisam ja tvoje djače da odgovaram na pitanja. Ako imaš nešto da napišeš napiši.
Kad smo već kod postavljanja pitanja, ni ti nisi odgovorio da li oni koji znaju kvantore dobijaju za pravo da krše aksiome struktura nad kojom vrše operacije, na primer pri leksikografskom uredjivanju ?
[ Nedeljko @ 21.07.2010. 09:21 ] @
Da, da, da. Sad se vadiš što ne znaš da odgovoriš.
Radi se o tome da odvlačiš temu na druga pitanja dok prethodno nije raspravljeno. Čim ti odgovoriš na moje, odgovaram ja na tvoja (koja su kasnije postavljena).
Možda se nismo razumeli. Možda ti misliš da se u nekom od koraka primenjuje neki stav ZFC koji nije dokaziv u ZF, a ne AC direktno (što je za mene sve jedno isto - primena AC direktno ili kroz nešto drugo). OK, hajmo ovako:
Koji korak ONOG dokaza ne prolazi u ZF?
Je li pitanje sada jasnije?
[ holononi @ 21.07.2010. 09:29 ] @
Sve prolazi u ZF ali usput povlači AC.
[ Nedeljko @ 21.07.2010. 09:38 ] @
Napokon si se izjasnio.
Ovo što si sad rekao znači da je AC posledica od ZF. Pol Koen je dokazao da to nije tačno.
Dobro, to je tvoje mišljenje. Možeš li da obrazložiš kako ovo usput povlači AC?
[ holononi @ 21.07.2010. 11:01 ] @
Ništa napokon. Te si odgovore dobio više puta:
http://www.elitesecurity.org/t405228-2#2650952
http://www.elitesecurity.org/t405228-2#2651351
http://www.elitesecurity.org/t405228-2#2651154
A što se tiče Koenovog dokaza ne interpretiraš ga u potpunosti jer isto važi i za negaciju.
To što ti nazivaš leksikografsko uredjenje nije ništa drugo nego funkcija izbora. Pa tebi ostaje da oboriš stav da su funkcija izbora i AC ekvivalentni. [ Nedeljko @ 21.07.2010. 12:05 ] @
Da se negacija AC ne može dokazati u ZF nije dokazao Pol Koen, nego Kurt Gedel.
Funkcija izbora nije stav (iskaz), nego funkcija, pa ne može biti ekvivalentna stavu (iskazu).
[ holononi @ 21.07.2010. 12:44 ] @
Ko kaže da je dokazao Koen a ne Gedel ?
Ako se iz nekog niza formula može izvesti formalan zaključak AC onda to nije u suprotnosti sa tvrdjenjem na koje se ti pozivaš. Tada se može zaključiti da dokaz u stvari nikad nije ni bio u ZF.
[ Nedeljko @ 21.07.2010. 13:48 ] @
Da li je dokaz u ZF zaključuje se samo na osnovu upotrebljenih aksioma i ničega više.
Baš bih voleo da vidim kako ćeš odande da izvedeš da postoji funkcija izbora na P(R)\{0} (ili dobro uređenje na R ako ti se više sviđa).
[ holononi @ 21.07.2010. 14:10 ] @
To zadovoljstvo prepuštam tebi a ja ću da se pozovem na aksiom izbora i da posetim debelu ladovinu jer je kod mene minimum +35.
U medjuvremenu predlažem da neko otvori novu diskusiju jer je po ovome rečeno dovoljno tako da sumnjam da ćemo rešiti probleme koje nisu rešili ni profesionalci u ovom polju.
[ Nedeljko @ 21.07.2010. 14:40 ] @
Pa, ne mogu ja da dokazujem tvoje stavove. Ti si tvrdio da odatle sledi AC, a ne ja.
U Koenovom simetričnom podmodelu generičkog proširenja (koji zadovoljava sve ZF aksiome) se R ne može dobro urediti.
[ Nedeljko @ 21.07.2010. 17:58 ] @
Ono što ti ne možeš da shvatiš je sitna razlika između pojedinačnog i opšteg - ako se jedan skup, na primer N x N, može dobro urediti, to nikako ne znači da se svaki skup može dobro urediti, tj. da važi AC. Odnosno da u ZF važi AC u nekim specijalnim slučajevima, mada nije dokazivo da važi u opštem slučaju.
[ holononi @ 21.07.2010. 18:25 ] @
Ne tvrdim da u ZF važi AC. Pročitaj komentare nakon što si se pozvao na Koenov dokaz ( http://www.elitesecurity.org/t405228-5#2653339).
Nema potrebe da se dalje vrtimo u krug.
http://www.elitesecurity.org/t405228-4#2652395
[ Nedeljko @ 21.07.2010. 20:19 ] @
Tvrdiš da iz onog dokaza sledi AC, pa bi mogao to i da demonstriraš.
[ holononi @ 21.07.2010. 21:24 ] @
Kako se teorema može dokazati eksperimentalno ?
[ Nedeljko @ 21.07.2010. 21:55 ] @
Ko je to rekao?
Demonstracija = izvođenje.
[ holononi @ 22.07.2010. 04:43 ] @
Pardon, napisao sam komentar u pogrešnoj temi.
[ Nedeljko @ 22.07.2010. 08:44 ] @
I gde se dede izvođenje AC iz onog dokaza?
Kako ćeš odande da zaključiš da se npr. R može dobro urediti?
[ holononi @ 22.07.2010. 09:13 ] @
Evo formulacije aksiome izbora koja se pripisuje Zermelu (1904):
Ako je E jedna familija skupova koji nisu prazni i bez zajedničkih elemenata dva po dva, onda postoji bar jedan skup S koji sadrži jedan element i samo jedan svakog od skupova familije E.
Iz ovog ne vidim nikakve probleme sa kvantorima na koje se ti pozivaš.
[ Nedeljko @ 22.07.2010. 09:23 ] @
Evo, neka je
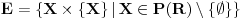 .
Izvedi iz onog dokaza da postoji traženi skup  . [ holononi @ 22.07.2010. 12:51 ] @
Ništa od kvantora, ništa od Koena, pozdrav i
[ Nedeljko @ 22.07.2010. 14:12 ] @
Ništa od odgovora na konkretno pitanje.
[ peksimit @ 22.07.2010. 15:08 ] @
@ Nedeljko
idi radi nesto, pusti coveka na miru...
[ boxxter @ 22.07.2010. 15:53 ] @
Ja sam postavio ovu temu, da bih ukazao na neke mane formalnog obrazovanja danas.
Nedeljko je na primer fakultetski obrazovan covek, koji je rekao da je Dostojevski zabavljac, Nobelovac Bertrand Rasel je glup I ne razume matematiku, Tolstoj je obican davez, Edvard Viten je za UltraMad Zone, Stiven Havking nije bas neki fizicar, anticki filozofi su prevazidjeni, a problem sa realtivistickom masom je samo u nasim glavama, i istina o necemu je stvar naseg dogovora.
Hteo sam samo da ukazem na to, koliko mana ima bubanje cinjenica, kad covek ne shvata i ne ulazi u sustinu, i koliki to zaostatak cini za savremenim naucnim dostignucima. Interesantna je sujeta koja je proizvod ovakvog stava, a i bes i agresivnost.
[ Nedeljko @ 22.07.2010. 16:07 ] @
Dostojevski: Da, meni je zanimljiv. Nemam šta da komentarišem oko njega.
Rasel: Nisam rekao da je glup, ali to što je neko dobio Nobelovu nagradu za književnost ne znači da razume matematiku.
Tolstoj: To što je neko popularan, ne znači da nekima nije dosadan.
Viten: Ne znam zašto je ON za UMZ, ali neke rasprave koje su se ovde vodile jesu.
Stiven Hoking: I pored sve popularnosti nije dobio ni Nobelovu nagradu, ni Lorencovu medalju. Zašto?
Antika: Mnogo je vode od onda proteklo.
Relativistička masa: Objasnila je i defekt mase atomskih jezgara i oslobađanje energije pri nuklearnim reakcijama, a ta je formula itekako potvrđena i u akceleratorima.
Poslednje: Da li je definicija transcedentnog broja kao broja koji nije algebarski istinita?
[ boxxter @ 22.07.2010. 17:40 ] @
Citat: Nedeljko:Rasel: Nisam rekao da je glup, ali to što je neko dobio Nobelovu nagradu za književnost ne znači da razume matematiku.
Ovo sto si sad napisao dovoljno govori samo za sebe, tako da necu da komentarisem, samo cu da te citiram.
Citat: Nedeljko:Rasel je poznat po raznim glupostima
Ovo je divna izjava.
Citat: Nedeljko: Dostojevski: Da, meni je zanimljiv. Nemam šta da komentarišem oko njega.
Zanimljivo je da pisca koji je olicenje duhovnosti u knjizevnom svetu, gledas kao zabavljaca. Nedostatak postovanja, ili arogancija? Postujem bezobzirnost, ali to je licna odluka svakog coveka.
Citat: @nedeljko@ Pa, normalno je da književnost čitam iz zabave. Nego zbog čega?
Da. Citaj iz zabave. I oni su se zabavljali dok su pisali. I pisali su da bi te zabavili. Recimo kao narodna muzika sa pinka.
Citat: Nedeljko: Tolstoj: To što je neko popularan, ne znači da nekima nije dosadan. Citat: Za mene je Tolstoj običan davež i ništa više od toga.
Nista vise od toga? To je tvoja analiticnost?
Citat: Viten: Ne znam zašto je ON za UMZ, ali neke rasprave koje su se ovde vodile jesu.
Hoces da te podsetim kako si rekao da su alternativne teorije sarlatanske i debilne? Na primer teorija struna?
Citat: Stiven Hoking: I pored sve popularnosti nije dobio ni Nobelovu nagradu, ni Lorencovu medalju. Zašto?
Interesantno pitanje si postavio.
Citat: Antika: Mnogo je vode od onda proteklo.
Nista gluplje nisam cuo. Pa temelji nauke koju proucavas su u antici. Pokusaj da je zaobidjes molim te, i da je ignorises. Bices kralj uzaludnog posla, i gubljenja vremena.
Citat: Relativistička masa: Objasnila je i defekt mase atomskih jezgara i oslobađanje energije pri nuklearnim reakcijama, a ta je formula itekako potvrđena i u akceleratorima.
Ti stvarno, jednostavno ne mozes da razumes u cemu je problem sa relativistickom masom, o kome je i Ajnstajn govorio.
Citat: Poslednje: Da li je definicija transcedentnog broja kao broja koji nije algebarski istinita?
Da li je definicija istinita, ili pojam? Jel ta definicija stvar naseg dogovora ili nam sama sustina pojma namece definiciju?
Ti jednostavno ne mozes da razumes to. [ Ivan Dimkovic @ 22.07.2010. 19:41 ] @
Sledeci ko bude trolovao na forumu Matematika bice banovan majke mi...
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|