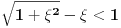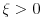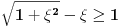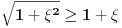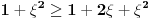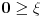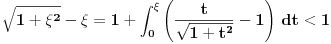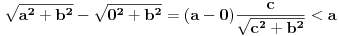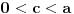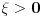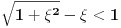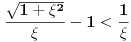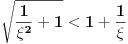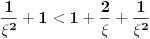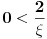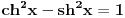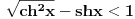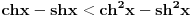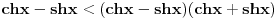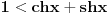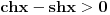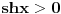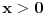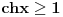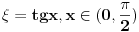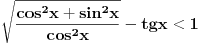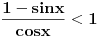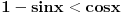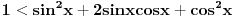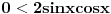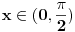[ petarm @ 27.07.2010. 16:00 ] @
|
[ Farenhajt @ 27.07.2010. 17:44 ] @
Način 2.
Prema razlici kvadrata, 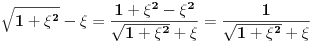 Pošto je za 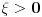 imenilac veći od jedan, onda je ceo izraz manji od jedan. imenilac veći od jedan, onda je ceo izraz manji od jedan.Način 3. Posmatrajmo pravougli trougao s katetama  i i 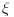 . Tada je po trougaonoj nejednakosti hipotenuza manja od zbira kateta: . Tada je po trougaonoj nejednakosti hipotenuza manja od zbira kateta: 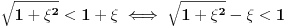 Način 4. Uvedimo smenu 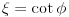 . Tada . Tada 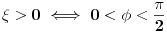 i i 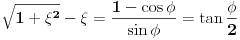 . Pošto je . Pošto je 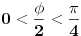 , imamo , imamo 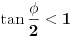 Način 5. Posmatrajmo vektore 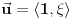 i i 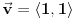 . Pošto je . Pošto je 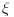 pozitivno, ugao između njih, po apsolutnoj vrednosti, mora biti manji od pozitivno, ugao između njih, po apsolutnoj vrednosti, mora biti manji od 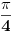 - ugao između - ugao između 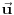 i apscise pripada intervalu i apscise pripada intervalu 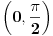 , a ugao između , a ugao između 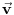 i apscise je tačno i apscise je tačno 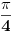 . .Dakle, 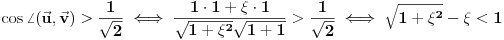 [ Nedeljko @ 27.07.2010. 20:59 ] @
Koji je smisao dokazivanja nečeg krajnje elementarnog na što više načina?
[ Farenhajt @ 27.07.2010. 21:21 ] @
Citat: Nedeljko: Koji je smisao dokazivanja nečeg krajnje elementarnog na što više načina? Pošto ti je ovo besmislena tema, prođi je se ti u širokom luku (ne traći svoje dragoceno vreme), nego kao smislen čovek 'vataj lepo u kolo svoje omiljene pretplatnike pa opaljuj novu epizodu višegodišnje perpetualne psihodramske telenovele, a nas besmislene pusti kraju da se sami zabavljamo kako siroti ograničeni umemo. Način 6. Neka je 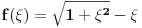 . Pošto je . Pošto je 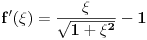 , na intervalu , na intervalu 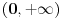 imamo da je imamo da je 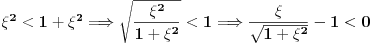 . Prema tome, funkcija je monotono opadajuća, pa u svakoj tački pomenutog intervala njena vrednost mora biti manja nego u nuli, a . Prema tome, funkcija je monotono opadajuća, pa u svakoj tački pomenutog intervala njena vrednost mora biti manja nego u nuli, a 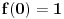 . .Način 7. Uvedimo smenu 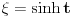 , gde , gde 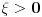 povlači povlači 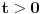 . Tada . Tada 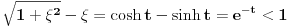 [ Nedeljko @ 27.07.2010. 22:36 ] @
[ holononi @ 28.07.2010. 11:14 ] @
A jel može da se reši bez svodjenja na kontradikciju, mislim prostim prebacivanjem i kvadriranjem odakle se dobije 1 < 1 + 2ε, što važi jer je ε > 0 po uslovu zadatka ?
[ Kolins Balaban @ 28.07.2010. 13:23 ] @
pa to je uradjeno u prvom postu, ako ja dobro vidim....
[ holononi @ 28.07.2010. 15:06 ] @
U prvom postu je pretpostavljeno suprotno pa je svedeno na kontradikciju.
No ništa za to. Pretpostavimo da se nismo setili da kvadriramo. Prebaciti ε na drugu stranu, logaritmovati i malo srediti, zatim antilogaritmovati i svedeno je na prethodni slučaj, tj. kvadriranje je postalo očigledno kao posledica primenjenog metoda. [ Nedeljko @ 28.07.2010. 15:39 ] @
[ petarm @ 28.07.2010. 16:06 ] @
Citat: Nedeljko: Metod primenjen u prvom postu nije primenljiv na realne stepene, a primena Lagranžove teoreme jeste. Može i sa ovako kako holononi kaže, a postavljač teme bi mogao da prokomentariše zašto ju je postavio. Može se uvesti i smena 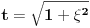 , pa se , pa se 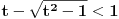 svodi na svodi na 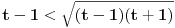 . .Mislim da je posle ovolike diskusije jasno zasto? Da se ljudi malo ukljuce. Stvar jeste trivijalna, al trivijalno je katkad zanimljivo. Svaki slozen zadatak se sastoji iz jako mnogo prostih. U svim ovim odgovorima nema prepucavanja koja izlaze iz domena matematike. Ima zanimljivih postova, a Farenhajt je cak uspeo i da me nasmeje! Citat: Farenhajt: Pošto ti je ovo besmislena tema, prođi je se ti u širokom luku (ne traći svoje dragoceno vreme), nego kao smislen čovek 'vataj lepo u kolo svoje omiljene pretplatnike pa opaljuj novu epizodu višegodišnje perpetualne psihodramske telenovele, a nas besmislene pusti kraju da se sami zabavljamo kako siroti ograničeni umemo. Sve u svemu od trivijalnog zadatka ispade lepa i posecena tema! [ holononi @ 28.07.2010. 16:12 ] @
√(1 + ε²) - ε < √(1 + 2ε + ε²) - ε = √(1 + ε)² - ε = 1 + ε - ε = 1
[ petarm @ 29.07.2010. 16:16 ] @
[ Nedeljko @ 29.07.2010. 17:56 ] @
Uzastopni koraci su ekvivalentni.
[ holononi @ 29.07.2010. 18:41 ] @
@petarm
Pošao sam od pretpostavke da je ksi veće od nule. Dobio sam da je 2/ksi veće od nule. Odnosno 2 > 0 što je tačno pa je i polazna nejednakost tačna. Da sam pošao od pretpostavke ksi < 0 dobio bih kontradikcijiu pa za ksi < 0 navedena nejednakost ne važi. Za ksi = 0 ne bih mogao da primenim taj metod jer deljenje nulom nije dozvoljeno. Evo još jedna varijanta sa hiperboličnim funkcijama. Neka je 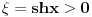 , tada , tada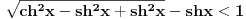 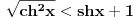 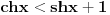 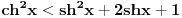 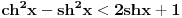 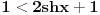 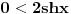 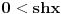 što važi za x > 0. što važi za x > 0.[ holononi @ 30.07.2010. 09:53 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|