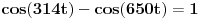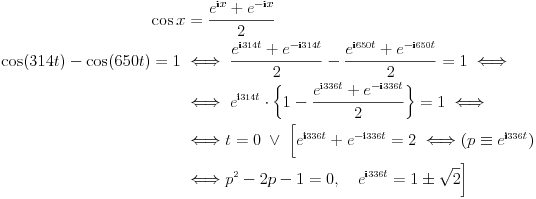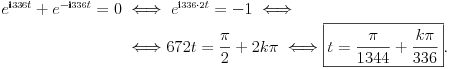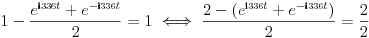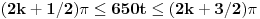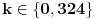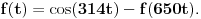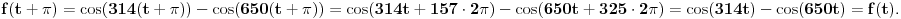[ paga @ 01.08.2010. 17:48 ] @
|
[ zzzz @ 01.08.2010. 19:24 ] @
Jesil probo sa ovim:
cos x - cos y = -2 sin( (x - y)/2 ) sin( (x + y)/2 ) ispašće nešto ovako sin(z)sin(z+a)=nešto Razvi sin zbira i napravi smjenu ,a onda se rješavaj korjenova. [ paga @ 02.08.2010. 07:55 ] @
Ništa ne dobijam,opet sin zavisi od t.
Ja treba da nađem t koje zadovoljava onu kosinusnu jednačinu. [ Cabo @ 02.08.2010. 09:48 ] @
[ paga @ 02.08.2010. 11:11 ] @
To je to.
Za k=0 , dobijem vreme u kojem se neke dve periode poklope u kojoj računam maksimalni napon. Hvala Cabo , mada mi opet nije jasna ova matematika . Naime .nije mi jasno odakle ovaj deo : e^i336t + e^-i336t =0 Hvala za rešenje [ Nedeljko @ 02.08.2010. 16:46 ] @
Ne bih se ja složio sa ovim rešenjem.
Prvo, ovaj prelaz ne valja Citat: Cabo: 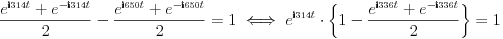 I u nastavku ima grešaka (ako je izraz u zagradi jednak jedinici, to ne znači da je ceo izraz sa leve strane jednakosti jednak jedinici), koje nisu bitne, jer se ionako oslanjaju na nešto pogrešno. [ Nedeljko @ 02.08.2010. 16:53 ] @
Ja lično ne vidim drugi način da se ovo reši, osim numerički.
[ Cabo @ 02.08.2010. 19:22 ] @
Tačno. Ne znam šta mi je bilo jutros pa sam ono napisao. Imao sam nameru da pomognem čoveku, ali izgleda da spavanje 5 sati dnevno uzima svoj danak.
Spremam Realne i kompleksne funkcije, i to mi je poslednji ispit. Pošizeo sam. [ epicentar @ 02.08.2010. 20:06 ] @
@Cabo
Izvinjavam se svima, ovo bi trebalo da bude privatna poruka, ali kao novopeceni clan nemam pravo na slanje iste kao takve. @Cabo Upravo pocinjem da spremam RiKF, stari statut, L-smer, matf-bg. Ukoliko ti ova recenica znaci nesto, mogli bismo, mozda, da razmenimo mail-ove... P.S. Uz par instrukcija mogu i da naucim da kucam... :) [ miki069 @ 03.08.2010. 01:20 ] @
@Cabo: što nisi čuvao Verovatnoću za kraj?
[ Cabo @ 03.08.2010. 10:12 ] @
Nemam pojma. :P
U principu, uvek sam radio prvo lakše stvari. [ Nedeljko @ 04.08.2010. 17:07 ] @
[ holononi @ 04.08.2010. 19:19 ] @
Budući da je
cos(314t) = 1 + cos(650t) sledi da cos(650t) < 0 (očigledno t ne može biti 0 ni Pi). Odnono Pi/2 < 650t < 3Pi/2 i 650t <> Pi. Jedno približno rešenje je t = -1/320.1075 a pošto je cos parna tada je i rešenje t = 1/320.1075 To sam dobio polovljenjem u 5-6 koraka ukucavajući u Google. [ Nedeljko @ 05.08.2010. 09:02 ] @
[ holononi @ 05.08.2010. 10:01 ] @
Uopšte nisam sporio tvoje rešenje. Samo sam primetio da se jednostavnim transformacijama dobije pored ostalog i
cos²(157t) = -cos(650t) pa je jasno da je leva strana sigurno nenegativna pa cos sa desne strana ne može biti pozitivan. Naravno rezultat bi trebalo uopštiti sa 2k*pi ali se ni tada ne bi dobila sva rešenja tako da sam to preskočio. Svaki pokušaj da se problem pojednostavi vodi u komplikacije ili vraća na početak. Na primer cos²(157t) = cos(pi)cos(650t) može da se vrti u nedogled. Slično i izrazima sa eksponencijalnom funkcijom. [ Nedeljko @ 05.08.2010. 10:22 ] @
Da.
[ holononi @ 05.08.2010. 11:45 ] @
Problem smo mogli svesti i na metod fiksne tačke jer je
cos(ax) - cosx = 1 odakle x = (1/a)arccos(1+cosx) [ Nedeljko @ 05.08.2010. 12:32 ] @
Evo, nove verzije programa.
Parametar Epsilon koji se ispisuje na kraju je udaljenost od nule najbliže vrednosti nuli od onih koje treba da budu različite od nule da bi broj rešenja bio tačno određen. Pošto je ta vrednost značajno veća od tačnosti upotrebljenog realnog tipa, rešenja na intervalu 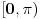 zaista ima tačno 1095. zaista ima tačno 1095.[ Nedeljko @ 05.08.2010. 20:51 ] @
Našao sam grešku u programu. Zapravo, ima 1149 rešenja.
[ h4su @ 07.08.2010. 19:25 ] @
Citat: Nedeljko: Funkcija 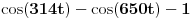 je očigledno je očigledno  -periodična, pa joj nule treba tražiti u intervalu -periodična, pa joj nule treba tražiti u intervalu 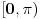 . .Prilažem program pisan na C++ jeziku, po m-M Calculus metodi S. Prešića, koji je lokalizovao 1095 rešenja uz napomenu da greška računa nije uzeta u obzir, tako da rezultat ne treba uzeti zdravo za gotovo. Meni nije jasno kako je ova funkcija pi periodicna, zar nije 2pi periodicna. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|