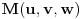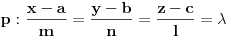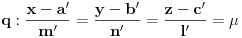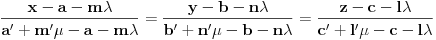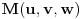
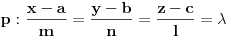
Neka je , i

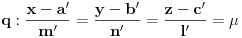
Provuci pravu kroz tačke datih pravih koje odgovaraju nekim vrednostima parametara i , a onda postavi uslov da ta prava prolazi kroz tačku i reši dobijene jednačine po i .





.

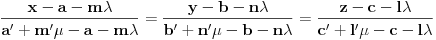
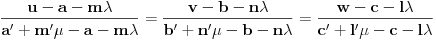
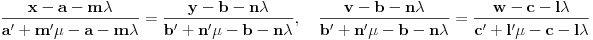
Dobio si sistem dve linearne jednačine po dvema nepoznatim i .

Mogao si da radiš i onako kako si počeo, ali pošto vektor prave nije jednoznačno određen, već do na kolinearnost, onda je normalno da ćeš dobiti dve jednačine po njegovim trima koordinatama.

Hvala Nedjeljko, a uspio sam rijesiti i na onaj prvi nacin. dvije jednacine a tri nepoznate, rjesenja izrazim preko jedne nepoznate a posto je rjesenje ustvari vektro polozaja trazene prave na kraju samo podijelim rjesenje sa tom nepozatom,tj eliminisem je.
hvala jos jednom...

To je bio algebarski pristup, a evo i geometrijskog:

Trazena prava, oznacimo je sa m, pripada kako ravni odredjenoj sa M i p, tako i ravni odredjenoj sa M i q.
Prema tome, m pripada preseku ravni Mp i Mq.

Lepota je u tome sto se vektor pravca trazene prave dobija vektorskim proizvodom vektora polozaja (normale) ove dve ravni.
Ovo je zato sto je presecna prava dveju ravni normalna na vektore polozaja te dve ravni, a vektorski proizvod upravo daje takav vektor.

Vektor polozaja ravni Mp i Mq takodje mozemo naci vektorskim proizvodom:
ako je P proizvoljna tacka prave P, onda je MP x p potreban vektor polozaja ravni Mp;
na isti nacin je MQ x q vektor polozaja ravni Mq, gde je Q proizvoljna tacka prave q.

Na kraju, vektor pravca trazene prave se dobija kao:
(MP x p) x (MQ x q).

Darkosos,
mozes li nam postaviti crtez geometrijskog pristupa,mislim da bi dobro dosao,cisto zbog razumijevanja materije.

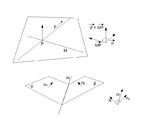
Pokusacu nesto...

Primetimo jos da je uslov da prava m sece p i q iskoriscen samo da bi se doslo do sireg skupa - ravni, u kojem se mora nalaziti, pa tako krajnja formula daje resenje cak i onda kada ono ne postoji :) Npr. kada su p i q paralelne a M van ravni pq.

Najbolje je pretpostaviti da p i q nisu paralelne i da M nije ni na jednoj od njih. Mrzucka me sad da ispisujem analizu mogucih slucajeva.