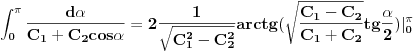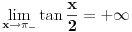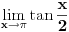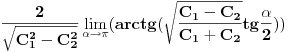[ petarm @ 07.08.2010. 09:54 ] @
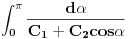 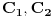 - konstante - konstantesmena: 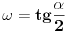 dobija se 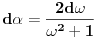 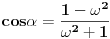 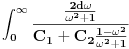 Malo sam se ovde zbunio oko gornje granice. Posto 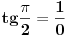 nije definisano. Posto integral ne oseca jednu tacku ja smem da uzmem neku blisku tacku ovoj i fakticki da mi gornja granica bude nije definisano. Posto integral ne oseca jednu tacku ja smem da uzmem neku blisku tacku ovoj i fakticki da mi gornja granica bude  . Jesam li u pravu? . Jesam li u pravu?http://www.intmath.com/Trigono...-cotangent-secant-cosecant.php [Ovu poruku je menjao petarm dana 07.08.2010. u 12:33 GMT+1] |