[ Hard_Rock_Fan @ 11.08.2010. 13:58 ] @
| Imam funkciju sa apsolutnom vrednoscu i nisam siguran kako da nadjem prvi izvod. Moze neka pomoc?:D Hvala! Funkcija glasi: f(x)=x^3-2x|x-2|. Predpostavljam da je jednostavno.:) Pozdrav! |
|
[ Hard_Rock_Fan @ 11.08.2010. 13:58 ] @
[ atomant @ 11.08.2010. 16:41 ] @
Ostatak izvoda je prilicno lak, tako da verujem da imas samo problem sa nalazenjem izvoda ove apsolutne zagrade.
Jedan mali trik. Recimo da je ono sto je u apsolutnoj zagradi neka nova promenljiva, recimo t: 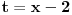 Pri tome znas da vazi da je 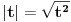 . . Dakle, 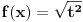 . Izvod trazis na sledeci nacin, preko lancanog pravila: . Izvod trazis na sledeci nacin, preko lancanog pravila: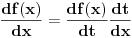 , gde je , gde je 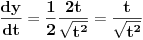 , a , a 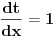 Odatle sledi da je 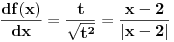 . Odavde je lako. . Odavde je lako.Trazeni izvod je: 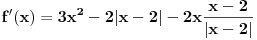 [ Nedeljko @ 11.08.2010. 19:01 ] @
[ Hard_Rock_Fan @ 11.08.2010. 19:17 ] @
Hvala na odgovorima!:)
@Nedeljko... Prvi izvod bi samo bio 3x^2-4x+4 odnosno 3x^2+4x-4. [ atomant @ 11.08.2010. 20:24 ] @
sto se opet moze dobiti iz onog izraza gore
[ Nedeljko @ 11.08.2010. 21:38 ] @
Citat: Hard_Rock_Fan: @Nedeljko... Prvi izvod bi samo bio 3x^2-4x+4 odnosno 3x^2+4x-4. Jok, nego drugi izraz levo od dvojke, a prvi desno. [ holononi @ 11.08.2010. 22:02 ] @
Nedeljkov metod rešavanja se najčešće primenjuje mada je automat priložio veoma zanimljiv metod.
Nije mi jasno kako je Nedeljko dobio slobodan član 2 odnosno -2. [ Hard_Rock_Fan @ 11.08.2010. 22:47 ] @
Potpuno sam saglasan sa holononijem. I ja mislim da slobodan clan nije i ne moze da bude 2 odnosno -2.
[ atomant @ 11.08.2010. 22:58 ] @
da, trebalo bi 4 i -4.
[ Nedeljko @ 11.08.2010. 23:04 ] @
Da, i ja sad vidim. No, najvažnije je da je zadatak razjašnjen.
[ nightowl @ 11.06.2013. 18:14 ] @
[ number42 @ 11.06.2013. 18:25 ] @
i mene ovo zanima.
nisam se bas puno petljao s izvodima, ali nekako mi logicno da nikada ne stavljas apsolutnu vrednost tokom sredjivanja bilo kog izraza (ako vec nije data), nego uvek na kraju, ako treba da dobijes npr 2 resenja. [ Nedeljko @ 11.06.2013. 18:48 ] @
nightowl
Koren je definisan samo za nenegativne vrednosti argumenta. Dakle, funkcija nije ni definisana kada je potkorena veličina negativna, pa ti ne treba apsolutna vrednost. [ nightowl @ 11.06.2013. 18:56 ] @
Sasvim logicno. Hvala.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|